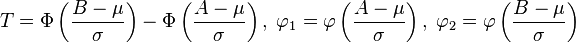正态分布
(
Normal distribution
)又名
高斯分布
(
Gaussian distribution
),是一个在
数学
、
物理
及
工程
等
领域
都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
若
随机变量
X
服从一个
数学期望
为
μ
、
标准方差
为
σ
2
的高斯分布,记为:
-
X
∼
N
(μ,σ
2
),
则其
概率密度函数
为
正态分布的
期望值
μ
决定了其位置,其
标准差
σ
决定了分布的幅度。因其曲线呈钟形,因此人们又经常称之为
钟形曲线
。我们通常所说的
标准正态分布
是
μ = 0,σ = 1
的正态分布(见右图中绿色曲线)。
目录
|
[
编辑
]
概要
正态分布是
自然科学
与
行为科学
中的定量现象的一个方便模型。各种各样的
心理学
测试分数和
物理
现象比如
光子
计数都被发现近似地服从正态分布。尽管这些现象的根本原因经常是未知的, 理论上可以证明如果把许多小作用加起来看做一个变量,那么这个变量服从正态分布(在R.N.Bracewell的Fourier transform and its application中可以找到一种简单的证明)。正态分布出现在许多区域
统计
:例如,
采样分布
均值
是近似地正态的,既使被采样的样本总体并不服从正态分布。另外,常态分布
信息熵
在所有的已知均值及方差的分布中最大,这使得它作为一种
均值
以及
方差
已知的分布的自然选择。正态分布是在统计以及许多统计测试中最广泛应用的一类分布。在
概率论
,正态分布是几种连续以及离散分布的
极限分布
。
[
编辑
]
历史
常态分布最早是
亚伯拉罕·棣莫弗
在
1734年
发表的一篇关于
二项分布
文章中提出的。
拉普拉斯
在1812年发表的《分析概率论》(
Theorie Analytique des Probabilites
)中对棣莫佛的结论作了扩展。现在这一结论通常被称为
棣莫佛-拉普拉斯定理
。
拉普拉斯在
误差分析
试验中使用了正态分布。
勒让德
于
1805年
引入
最小二乘法
这一重要方法;而
高斯
则宣称他早在
1794年
就使用了该方法,并通过假设误差服从正态分布给出了严格的证明。
“钟形曲线”这个名字可以追溯到
Jouffret
他在
1872年
首次提出这个术语”钟形曲面”,用来指代
二元正态分布
(
bivariate normal
)。正态分布这个名字还被
Charles S. Peirce
、
Francis Galton
、
Wilhelm Lexis
在1875分布独立的使用。这个术语是不幸的,因为它反应和鼓励了一种谬误,即很多概率分布都是正态的。(请参考下面的“实例”)
这个分布被称为“正态”或者“高斯”正好是
Stigler名字由来法则
的一个例子,这个法则说“没有科学发现是以它最初的发现者命名的”。
[
编辑
]
正态分布的定义
有几种不同的方法用来说明一个随机变量。最直观的方法是
概率密度函数
,这种方法能够表示随机变量每个取值有多大的可能性。
累积分布函数
是一种概率上更加清楚的方法,但是非专业人士看起来不直观(请看下边的例子)。还有一些其他的等价方法,例如
cumulant
、
特征函数
、
动差生成函数
以及cumulant-
生成函数
。这些方法中有一些对于理论工作非常有用,但是不够直观。请参考关于
概率分布
的讨论。
[
编辑
]
概率密度函数
正态分布
的
概率密度函数
均值为
μ
方差
为
σ
2
(或
标准差
σ
)是
高斯函数
的一个实例:
-
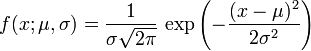
。
(
请看
指数函数
以及
π
.
)
如果一个
随机变量
X
服从这个分布,我们写作
X
~
N
(μ,σ
2
)
. 如果
μ = 0
并且
σ = 1
,这个分布被称为
标准正态分布
,这个分布能够简化为
-

。
右边是给出了不同参数的正态分布的函数图。
正态分布中一些值得注意的量:
- 密度函数关于平均值对称
-
平均值是它的
众数
(statistical mode)以及
中位数
(median) -
函数曲线下68.268949%的面积在平均值左右的一个
标准差
范围内 -
95.449974%的面积在平均值左右两个标准差
2σ
的范围内 -
99.730020%的面积在平均值左右三个标准差
3σ
的范围内 -
99.993666%的面积在平均值左右四个标准差
4σ
的范围内 -
反曲点
(inflection point)在离平均值的距离为标准差之处
[
编辑
]
累积分布函数
累积分布函数
是指随机变量
X
小于或等于
x
的概率,用密度函数表示为
正态分布的累积分布函数能够由一个叫做
误差函数
的
特殊函数
表示:
标准正态分布的累积分布函数习惯上记为
Φ
,它仅仅是指
μ = 0
,
σ = 1
时的值,
将一般正态分布用
误差函数
表示的公式简化,可得:
它的
反函数
被称为反误差函数,为:
该分位数函数有时也被称为
probit
函数。
probit
函数已被证明没有初等原函数。
正态分布的
分布函数
Φ(
x
)没有解析表达式,它的值可以通过
数值积分
、
泰勒级数
或者
渐进序列
近似得到。
[
编辑
]
生成函数
[
编辑
]
动差生成函数
动差生成函数
被定义为
exp(
tX
)
的期望值。
正态分布的矩生成函数如下:
可以通过在指数函数内配平方得到。
[
编辑
]
特征函数
特征函数
被定义为
exp(
itX
)
的
期望值
,其中
i
是虚数单位. 对于一个正态分布来讲,特征函数是:
把矩生成函数中的
t
换成
it
就能得到特征函数。
[
编辑
]
性质
正态分布的一些性质:
-
如果
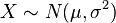
且
a
与
b
是
实数
,那么
aX
+
b
∼
N
(
a
μ +
b
,(
a
σ)
2
)
(参见
期望值
和
方差
). -
如果

与

是
统计独立
的正态
随机变量
,那么:-
它们的和也满足正态分布
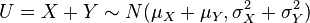
(
proof
). -
它们的差也满足正态分布

. -
U
与
V
两者是相互独立的。
-
它们的和也满足正态分布
-
如果

和
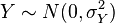
是独立正态随机变量,那么:-
它们的积
XY
服从概率密度函数为
p
的分布-
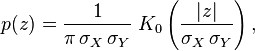
其中
K
0
是贝塞尔函数(modified Bessel function)
-
-
它们的比符合
柯西分布
,满足
X
/
Y
∼Cauchy(0,σ
X
/ σ
Y
)
.
-
它们的积
-
如果

为独立标准正态随机变量,那么
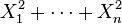
服从自由度为
n
的
卡方分布
。
[
编辑
]
标准化正态随机变量
[
编辑
]
矩(英文:moment)
一些正态分布的一阶动差如下:
| 阶数 | 原点矩 | 中心矩 | 累积量 |
|---|---|---|---|
| 0 | 1 | 0 | |
| 1 |
μ |
0 |
μ |
| 2 |
μ 2 + σ 2 |
σ 2 |
σ 2 |
| 3 |
μ 3 + 3μσ 2 |
0 | 0 |
| 4 |
μ 4 + 6μ 2 σ 2 + 3σ 4 |
3σ 4 |
0 |
正态分布的所有二阶以上的
累积量
为零。
[
编辑
]
生成正态随机变量
[
编辑
]
中心极限定理
正态分布有一个非常重要的性质:在特定条件下,大量
统计独立
的随机变量的和的分布趋于正态分布,这就是
中心极限定理
。中心极限定理的重要意义在于,根据这一定理的结论,其他概率分布可以用正态分布作为近似。
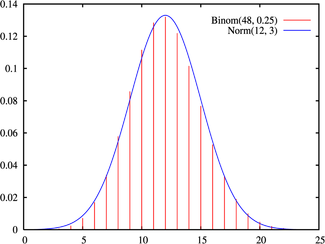
-
参数为
n
和
p
的
二项分布
,在
n
相当大而且
p
不接近1或者0时近似于正态分布(有的参考书建议仅在
np
与
n
(1 −
p
)
至少为5时才能使用这一近似)。
近似正态分布平均数为
μ =
np
且方差为
σ
2
=
np
(1 −
p
)
.
-
一
泊松分布
带有参数
λ
当取样样本数很大时将近似正态分布
λ
.
近似正态分布平均数为
μ = λ
且方差为
σ
2
= λ
.
这些近似值是否完全充分正确取决于使用者的使用需求
[
编辑
]
无限可分性
正态分布是
无限可分
的概率分布。
[
编辑
]
稳定性
正态分布是严格
稳定
的概率分布。
[
编辑
]
标准偏差
在实际应用上,常考虑一组数据具有近似于
正态分布
的概率分布。若其假设正确,则约68%数值分布在距离平均值有1个标准差之内的范围,约95%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为”68-95-99.7法则”或”经验法则”.
[
编辑
]
正态测试
[
编辑
]
相关分布
-
R
∼Rayleigh(σ)
是
瑞利分布
,如果
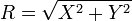
,这里
X
∼
N
(0,σ
2
)
和
Y
∼
N
(0,σ
2
)
是两个独立正态分布。 -

是
卡方分布
具有
ν
自由度
,如果
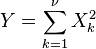
这里
X
k
∼
N
(0,1)
其中
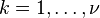
是独立的。 -
Y
∼Cauchy(μ = 0,θ = 1)
是
柯西分布
,如果
Y
=
X
1
/
X
2
,其中
X
1
∼
N
(0,1)
并且
X
2
∼
N
(0,1)
是两个独立的正态分布。 -
Y
∼Log-N(μ,σ
2
)
是
对数正态分布
如果
Y
=
e
X
并且
X
∼
N
(μ,σ
2
)
. -
与
Lévy skew alpha-stable分布
相关:如果

因而
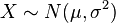
.
-
如果
X
是一个正态分布的随机变量,
Y
= |
X
|
,那么
Y
具有
折叠正态分布
.
[
编辑
]
参量估计
[
编辑
]
参数的极大似然估计
[
编辑
]
概念一般化
多元正态分布
的
协方差矩阵
的估计的推导是比较难于理解的。它需要了解
谱原理
(spectral theorem)以及为什么把一个
标量
看做一个1×1 matrix的trace而不仅仅是一个标量更合理的原因。请参考
协方差矩阵的估计
(estimation of covariance matrices).
[
编辑
]
参数的矩估计
[
编辑
]
常见实例
[
编辑
]
光子计数
[
编辑
]
计量误差
《饮料装填量不足与超量的概率》
某饮料公司装瓶流程严谨,每罐饮料装填量符合平均600毫升,标准差3毫升的常态分配法则。随机选取一罐,容量超过605毫升的概率?容量小于590毫升的概率
容量超过605毫升的概率 = p ( X > 605)= p ( ((X-μ) /σ) > ( (605 – 600) / 3) )= p ( Z > 5/3) = p( Z > 1.67) = 0.9525
容量小于590毫升的概率 = p (X < 590) = p ( ((X-μ) /σ) < ( (590 – 600) / 3) )= p ( Z < -10/3) = p( Z < -3.33) = 0.0004
《6-标准差(6-sigma或6-σ)的品质管制标准》
6-标准差(6-sigma或6-σ),是制造业流行的品质管制标准。在这个标准之下,一个标准常态分配的变量值出现在正负三个标准差之外,只有2* 0.0013= 0.0026 (p (Z < -3) = 0.0013以及p(Z > 3) = 0.0013)。也就是说,这种品质管制标准的产品不良率只有万分之二十六。假设例3-16的饮料公司装瓶流程采用这个标准,而每罐饮料装填量符合平均600毫升,标准差3毫升的常态分配法则。预期装填容量的范围应该多少? 6-标准差的范围 = p ( -3 < Z < 3)= p ( – 3 < (X-μ) /σ < 3) = p ( -3 < (X- 600) / 3 < 3)= p ( -9 < X – 600 < 9) = p (591 < X < 609) 因此,预期装填容量应该介于591至609毫升之间。
[
编辑
]
生物标本的物理特性
[
编辑
]
金融变量
[
编辑
]
寿命
[
编辑
]
测试和智力分布
《计算学生智商高低的概率》
假设某校入学新生的智力测验平均分数与方差分别为100与12。那么随机抽取50个学生,他们智力测验平均分数大于105的概率?小于90的概率?
本例没有常态分配的假设,还好中心极限定理提供一个可行解,那就是当随机样本长度超过30,样本平均数xbar近似于一个常态变量,因此标准常态变量Z = (xbar –μ) /σ/ √n。
平均分数大于105的概率 = p(Z> (105 – 100) / (12 /√50))= p(Z> 5/1.7) = p( Z > 2.94) = 0.0016
平均分数小于90的概率 = p(Z< (90 – 100) / (12 /√50))= p(Z < 5.88) = 0.0000
[
编辑
]
计算统计应用
[
编辑
]
生成正态分布随机变量
在计算机模拟中,经常需要生成正态分布的数值。最基本的一个方法是使用标准的正态累积分布函数的反函数。除此之外还有其他更加高效的方法,Box-Muller变换就是其中之一。另一个更加快捷的方法是ziggurat算法。下面将介绍这两种方法。一个简单可行的并且容易编程的方法是:求12个在(0,1)上均匀分布的和,然后减6(12的一半)。这种方法可以用在很多应用中。这12个数的和是Irwin-Hall分布;选择一个方差12。这个随即推导的结果限制在(-6,6)之间,并且密度为12,是用11次多项式估计正态分布。
Box-Muller方法是以两组独立的随机数U和V,这两组数在(0,1]上均匀分布,用U和V生成两组独立的标准正态分布随即变量X和Y:
-
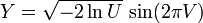
。
这个方程的提出是因为二自由度的
卡方分布
(见性质4)很容易由指数随机变量(方程中的lnU)生成。因而通过随机变量V可以选择一个均匀环绕圆圈的角度,用指数分布选择半径然后变换成(正态分布的)x,y坐标。
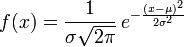



![\Phi(z)=\frac12 \left[1 + \mathrm{erf}\,(\frac{z-\mu}{\sigma\sqrt2})\right] .](http://upload.wikimedia.org/wikipedia/zh/math/3/0/9/309df22a79a5687e1891cfbcbae2db89.png)

![\Phi(z)=\frac{1}{2} \left[ 1 + \operatorname{erf} \left( \frac{z}{\sqrt{2}} \right) \right].](http://upload.wikimedia.org/wikipedia/zh/math/d/0/5/d052159a00aa278a29d101a5c2b59353.png)
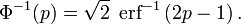
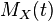
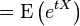



![=\mathrm{E}\left[ \exp(i t X)\right]](http://upload.wikimedia.org/wikipedia/zh/math/8/d/c/8dc3404119c0646f1675b63925836791.png)