博客

Given a connected, undirected graph G = (V, E), where V is the vertex set consisting a collection of nodes, and E is the set of edges, each of which connects two nodes from V. A vertex subset S is a separator if the subgraph induced by the vertices in V, but not in S, has two connected components. We shall use the notation [S, W, B] to represent the partition, where the removal of the separator S will give two connected components W and B.

In this problem, we consider the separators in grids. Each node in a grid is connected to its eight neighbors (if they exist). In Figure-1, we illustrate a partition of a 6*6 grid with a 9-point separator (gray nodes in the figure). The nodes on the left of the separator are in set W (white nodes), and the nodes on the right of the separator are in set B (black nodes).

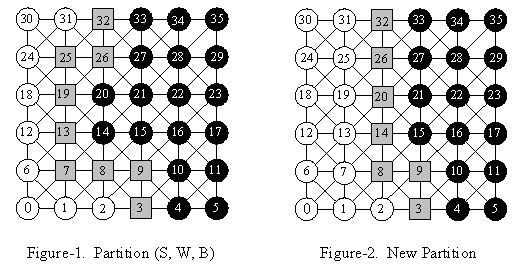
To simplify the problem, you can assume that all the separators referred in this problem satisfy the following restrictions:

1) It’s a minimal separator. A separator is minimal if no subset of it forms a separator.

2) It begins from a node on the top line of the grid, except the corner (i.e. 30 and 35 in the figures), and ends with a node on the bottom line of the grid, also except the corner (i.e. 0 and 5 in the figures).

3) On its way from top to bottom, it can go left, right or down, but never go up.

Now we describe a method to improve a given partition on a grid, through which we can reduce the number of nodes in the separator. This method contains two steps:

1) Select several nodes from B and add them into S. Any of the selected nodes must have a left neighbor which is in S.

2) Remove several nodes from S (excluding the nodes added in the former step), and add them into W.

After the improvement, we should ensure S is still a separator, and make the number of nodes in S as small as possible. As for Figure-1, we should add 14 and 20 into S, and remove 7, 13, 19 and 25 from S. After that, we obtain a new partition with a 7-point separator shown in Figure-2.

Your task is, given a partition on a grid, to determine the least number of nodes in the separator after the improvement.

There are several test cases. Each case begins with a line containing two integers, N and M (3 <= M, N <= 200). In each of the following N lines, there are M characters, describing the initial partition of the M*N grid. Every character is ‘S’, ‘W’ or ‘B’. It is confirmed that each of these three characters appears at least once in each line, and ‘W’s are always on the left of ‘S’s.

A test case of N = 0 and M = 0 indicates the end of input, and should not be processed.

For each test case, you should output one line containing one integer, which is the least number of nodes in the separator after the improvement.

6 6
WWSBBB
WSSBBB
WSBBBB
WSBBBB
WSSSBB
WWWSBB
0 0

7

Beijing 2004

题意是有一个图，左部分为W，右部分为B，用S分割，移动S，使S的总数最少。（题目中已说可以向左走，向右走，向下走，但不能向上走）。

#include <cstdio>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <map>
#include <string>
#include <stack>
#include <cctype>
#include <vector>
#include <queue>
#include <set>
#include <iomanip>

using namespace std;
//#define Online_Judge
#define outstars cout << "***********************" << endl;
#define clr(a,b) memset(a,b,sizeof(a))
#define lson l , mid  , rt << 1
#define rson mid + 1 , r , rt << 1|1
#define FOR(i , x , n) for(int i = (x) ; i < (n) ; i++)
#define FORR(i , x , n) for(int i = (x) ; i <= (n) ; i++)
#define REP(i , x , n) for(int i = (x) ; i > (n) ; i--)
#define REPP(i ,x , n) for(int i = (x) ; i >= (n) ; i--)
#define mid ((l + r) >> 1)
#define mk make_pair
const int MAXN = 200 + 10;
const int maxw = 10000000 + 20;
const int MAXNNODE = 10000 +10;
const long long LLMAX = 0x7fffffffffffffffLL;
const long long LLMIN = 0x8000000000000000LL;
const int INF = 0x7fffffff;
const int IMIN = 0x80000000;
#define eps 1e-8
#define mod 10007
typedef long long LL;
const double PI = acos(-1.0);
typedef double D;
typedef pair<int , int> pii;
struct point
{
    int x , y ;
    point(){}
    point(int y , int x):y(y) , x(x){}
};
int n, m[MAXN][MAXN] , vis[MAXN][MAXN];///m记录图形，vis记录S的数量
int M , d[3][2] = {{-1 , 0} , {1 , 0} , {0 , 1}};
int bfs(int i)
{
    queue <point> q;
    point tmp(1 , i);
    q.push(tmp);
    vis[1][i] = 1;
    while(q.size())
    {
        point u = q.front();
        q.pop();
        FOR(k , 0 , 3)
        {
            tmp.x = u.x + d[k][0];
            tmp.y = u.y + d[k][1];
            if(tmp.x > M||tmp.x <1)continue;
            if(tmp.y > n||tmp.y < 1)continue;
            if(vis[tmp.y][tmp.x]||!m[tmp.y][tmp.x])continue;
            vis[tmp.y][tmp.x] = vis[u.y][u.x] + 1;
            if(tmp.y == n)return vis[tmp.y][tmp.x];
            q.push(tmp);
        }
    }
}
int main()
{
    //ios::sync_with_stdio(false);
#ifdef Online_Judge
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
#endif // Online_Judge
    while(~scanf("%d%d" , &n , &M) , M||n)
    {
        char ch;
        clr(m , 0);
        REPP(i , n , 1)FORR(j , 1  ,M)
        {
            while((ch = getchar())!='W'&&ch != 'S' && ch != 'B');
            if(ch == 'S')
            {
                m[i][j] = 1;
                if((i == 1||i == n)&&j < M - 1)m[i][j + 1] = 1;
                else if(i > 1 && i < n && j < M)m[i][j + 1] = 1;
            }
        }
        int ans = INF;
        FORR(i , 1 , M)
        {
            if(m[1][i])
            {
                clr(vis , 0);
                ans = min(bfs(i) , ans);
            }
        }
        printf("%d\n" , ans);
    }
    return 0;
}