有序表查找算法简介
查找的是一个有序线性表,并进行查找操作的查找表
排序算法种类
按照算法复杂程度分类
这里主要以二分查找,插值查找,斐波那契查找为例子
二分查找
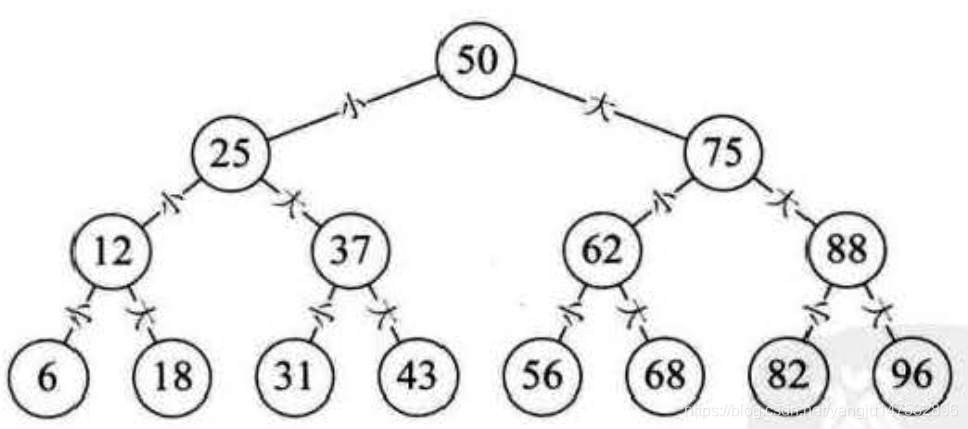
折半查找(Binary Search)技术,又称为二分查找。它的前提是线性表中的记录必须是关键码有序(通常从小到大有序),线性表必须采用顺序存储。折半查找的基本思想是:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功;若给定值小于中间记录的关键字,则在中间记录的左半区继续查找;若给定值大于中间记录的关键字,则在中间记录的右半区继续查找。
- 中心思想:有序取中,比较左右,折半查找。
算法
1 int Binary_Search(int *a,int n,int key)
2 {
3 int low,high,mid;
4 int low=1;
5 int high=n;
6 while(low<=high)
7 {
8 mid=(low+high)/2;
9 if(key<a[mid])
10 high=mid-1;
11 else if (key>a[mid])
12 1ow=mid+1;
13 else
14 return mid;
15 }
16 }
时间复杂度
具有n个结点的完全二又树的深度为
⌊
log
2
n
⌋
+
1
\lfloor \log _2n \rfloor +1
⌊
lo
g
2
n
⌋
+
1
。在这里尽管折半查找判定二叉树并不是完全二叉树,但同样相同的推导可以得出,最坏情况是查找到关键字或查找失败的次数为
⌊
log
2
n
⌋
+
1
\lfloor \log _2n \rfloor +1
⌊
lo
g
2
n
⌋
+
1
。
插值查找
插值查找(Interpolation Search)是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的查找方法,其核心就在于插值的计算公式
ke
y
−
a
[
l
o
w
]
a
[
h
i
g
h
]
−
a
[
l
o
w
]
\frac{key-a\left[ low \right]}{a\left[ high \right] -a\left[ low \right]}
a
[
h
i
g
h
]
−
a
[
l
o
w
]
k
e
y
−
a
[
l
o
w
]
。
- 中心思想:插值公式
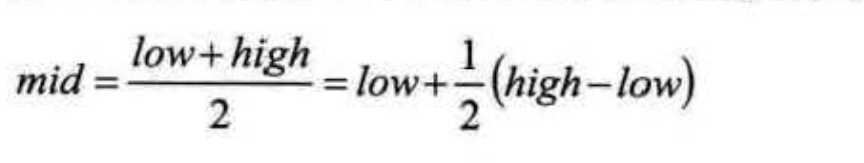
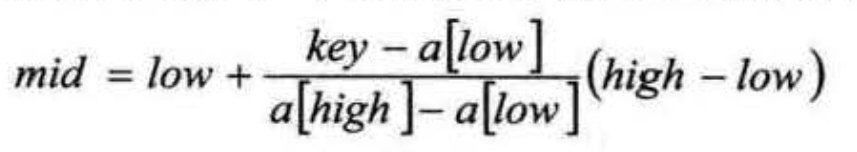
算法
1 int Interpolation_Search(int *a,int n,int key)
2 {
3 int low,high,mid;
4 int low=1;
5 int high=n;
6 while(low<=high)
7 {
8 mid=low+(high-1ow)*(key-a[low])/(a[highl-a[low]);/*插值改动处*/
9 if(key<a[mid])
10 high=mid-1;
11 else if (key>a[mid])
12 1ow=mid+1;
13 else
14 return mid;
15 }
16 }
时间复杂度
时间复杂度:O(logn)
斐波那契查找
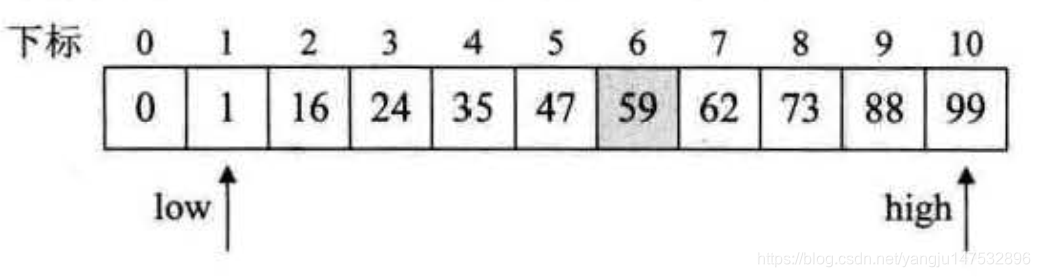
斐波那契查找(Fibonaci Search),它是利用了黄金分割原理来实现的。
- 中心思想:将线性表都成斐波那契数列,然后后黄金分割取上下限
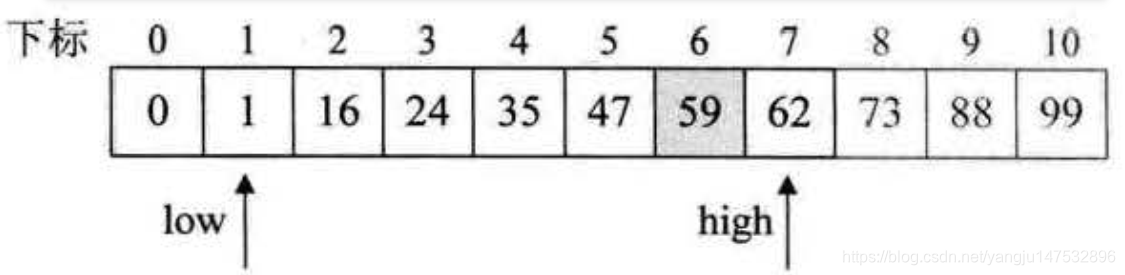
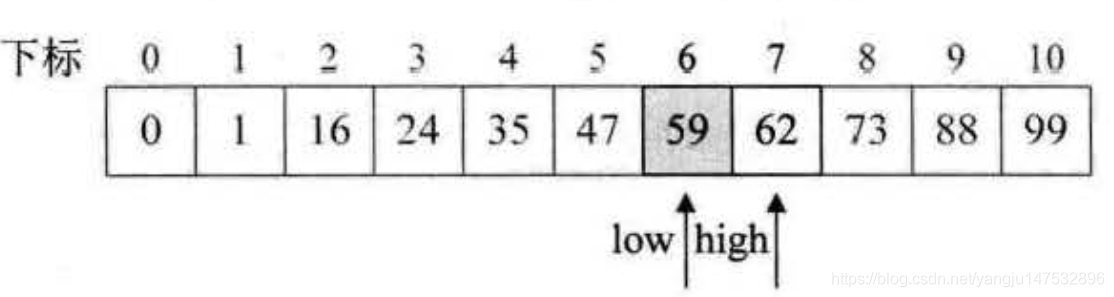
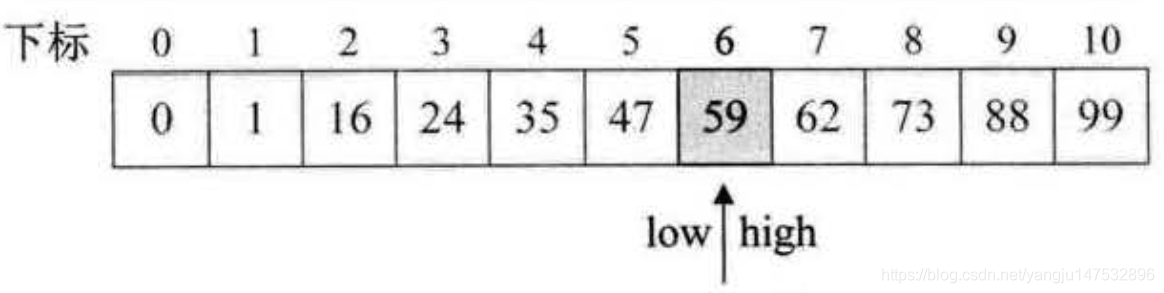
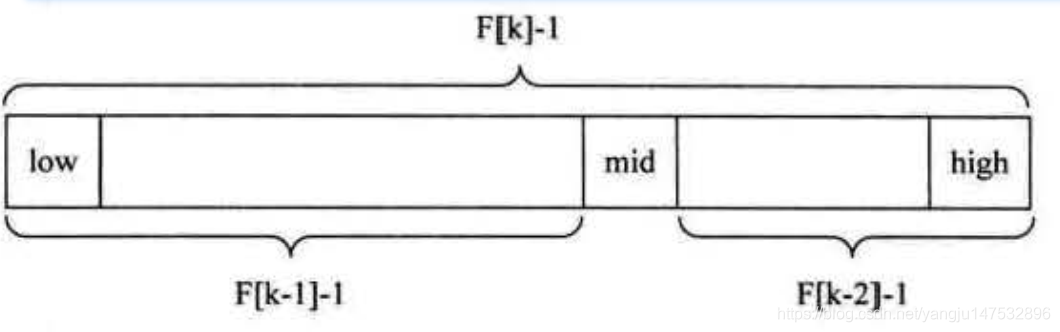
算法
1 int Fibonacci_Search(int *a,int n,int key)
2 {
3 int low,high,mid,i,k;
4 low=1;
5 high=n;
6 k=0;
7 while(n>F[k]-1)
8 k++;
9 for(i=n;i<=f[k]-1;i++)
10 a[i]=a[n];
11 while(low<=high)
12 {
13 mid=low+f[k-1]-1;
14 if(key<a[mid])
15 {
16 high=mid-1;
17 k=k-1;
18 }
19 else if(key>a[mid])
20 {
21 low=mid+1;
22 k=k-2;
23 }
24 else
25 {
26 if(mid<=n)
27 return mid;
28 else
29 return n;
30 }
31 }
32 return 0;
33 }
时间复杂度
尽管斐波那契查找的时间复杂也O(logn),但就平均性能来说,斐波那契查找要优于折半查找。可惜如果是最坏情况,比如这里key=1,那么始终都处于左侧长半区在查找,则查找效率要低于折半查找。
总结
- 应该说,三种有序表的查找本质上是分隔点的选择不同,各有优劣,实际开发时可根据数据的特点综合考虑再做出选择。
- 未知的数据首先考虑二分查找
- 均匀的数据适合插值查找
- 如果要查找的记录在右侧,则左侧的数据都不用再判断了,不断反复进行下去,对处于当中的大部分数据,斐波那契查找工作效率要高一些。
参考文献
[[1]] 程杰. 大话数据结构[M]. 清华大学出版社, 2011.
[[2]] 啊哈磊. 啊哈! 算法[M]. 人民邮电出版社, 2014.