数组求和与求积
数组求和——sum
S=sum(A,dim)
sum是求数组A指定方向的和。当dim=1时,求每一列的和,返回行向量。当dim=2时,求每一行的和,返回一个列向量。sum(A)默认dim=1。
S=sum(A,’ ‘)
‘ ’里面可以有‘default’、‘double’、‘native’、‘includenan’、‘omitnan’ 其中前三者规定了矩阵S的数据类型,includenan表示求和包含NaN,omitnan表示不包含NaN。注意每次只能加一个参数。
变式数组求和
S=nansum(A,dim)
不包含NaN的求和。与S=sum(A,‘omitnan’)相同。
B=cumsum(A,dim)
dim表示求和是按行求还是按列求,与sum相同,但求和方式不同。以按行求和为例,对每一行的数组[a
1
a
2
a
3
… a
n
],则所求的B的对应行
[b
1
b
2
b
3
… b
n
]满足b
k
=a
1
+a
2
+…+a
k
简而言之,就是求每个位置加上前面所有元素的和。
B=cumsum(A,’ ’ )
’ ‘中可填’forward’、‘reverse’、‘omitnan’ 或 ‘includenan’ 。其中
‘forward’、’reverse’表示求和方向,forward方向为默认方向,reverse表示相反方向,即在上述例子中b
k
=b
n
+b
n-1
+ … +b
k
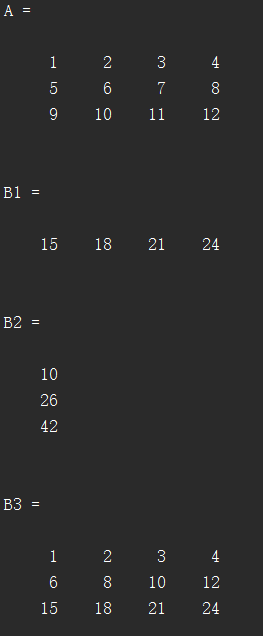
A=[1 2 3 4;5 6 7 8;9 10 11 12]
B1=sum(A)
B2=sum(A,2)
B3=cumsum(A)
B4=cumsum(A,2)
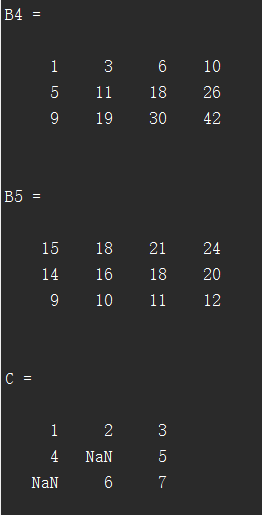
B5=cumsum(A,'reverse')
C=[1 2 3;4 NaN 5;NaN 6 7]
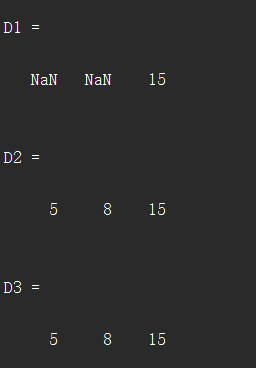
D1=sum(C)
D2=sum(C,'omitnan')
D3=nansum(C)
数组求积
求和与求积只是运算符号的差别。prod对应于sum;cumprod对应于cumsum。多了一个求阶乘的函数 factorial (n) 即求n!
求极限
| 命令 | 说明 |
|---|---|
|
l i m i t ( f ) limit(f) l i m i t ( f ) |
lim x → 0 f ( x ) \lim_{x\to 0}f(x) x → 0 lim f ( x ) |
|
l i m i t ( f , x , a ) limit(f,x,a) l i m i t ( f , x , a ) 或 l i m i t ( f , a ) limit(f,a) l i m i t ( f , a ) |
lim x → a f ( x ) \lim_{x\to a}f(x) x → a lim f ( x ) |
|
l i m i t ( f , x , a , ′ r i g h t ′ ) limit(f,x,a,'right') l i m i t ( f , x , a , ′ r i g h t ′ ) |
lim x → a + f ( x ) \lim_{x\to a^+}f(x) x → a + lim f ( x ) |
|
l i m i t ( f , x , a , ′ l e f t ′ ) limit(f,x,a,'left') l i m i t ( f , x , a , ′ l e f t ′ ) |
lim x → a − f ( x ) \lim_{x\to a^-}f(x) x → a − lim f ( x ) |
求导数
| 命令 | 说明 |
|---|---|
| diff(f) |
d f d x \dfrac{df}{dx} d x d f |
| diff(f,n) |
d n f d x n \dfrac{d^nf}{dx^n} d x n d n f |
| diff(f,x,n) |
∂ n f ∂ x n \dfrac{\partial^nf}{\partial x^n} ∂ x n ∂ n f |
求级数的和——symsum(f,x,a,b)
求函数f关于自变量x的从x=a到x=b的和,即
∑
x
=
a
b
f
(
x
)
\sum_{x=a}^b f(x)
x
=
a
∑
b
f
(
x
)
注:在MATLAB中
∞
\infty
∞
用 inf 表示