博客

DFT,FFT的算法原理见:https://zh.wikipedia.org/wiki/%E5%BF%AB%E9%80%9F%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2

#include <iostream>
#include <complex>
#include <cmath>
#include <vector>
#define eps 1e-6 
#define PI 3.14159265354
typedef std::complex<double> complex_t;
using namespace std;
 
//旋转因子的计算 
complex_t W(int k,int n,int N){
	return complex_t(cos(2*PI*k*n/N),-sin(2*PI*k*n/N));
}
 
//格式化 零 
complex_t format(complex_t &c){
	if(fabs(c.real())<eps) c.real()=0;
	if(fabs(c.imag())<eps) c.imag()=0;
	return c;
}
 
double format(double &c){
	if(fabs(c)<eps) c=0;
	return c;
}
 
//离散序列的DFT计算,只针对实数序列 ,完全按照DFT的公式来计算,O(n^2)的复杂度
void DFT(vector<double> &x_n,vector<complex_t> &X_k){
	X_k.clear();
	int N=x_n.size();
	for(int k=0;k<N;++k){
		complex_t t(0,0);
		for(int n=0;n<N;++n){
			t+=x_n[n]*W(k,n,N);
		}
		X_k.push_back(format(t));
	}
	
	int cnt=0;
	for(int i=0;i<N;++i){
		if(cnt==(int)sqrt(N)){
			cout<<endl;
			cnt=0;
		}
		++cnt;
		cout<<format(X_k[i])<<" ";
	}
	cout<<endl;
	
}
 
//IDFT的计算,只针对实数序列  
void IDFT(vector<complex_t> &X_k,vector<double> &x_n){
	x_n.clear();
	int N=X_k.size();
	for(int n=0;n<N;++n){
		complex_t t(0,0);
		for(int k=0;k<N;++k){
			t+=X_k[k]*W(k,-n,N);
		}
		x_n.push_back(t.real()/N);//运算结果只剩下实部 
		//cout<<(t/(double)N)<<endl; 
	}
	int cnt=0;
	for(int i=0;i<N;++i){
		if(cnt==(int)sqrt(N)){
			cout<<endl;
			cnt=0;
		}
		++cnt;
		cout<<format(x_n[i])<<" ";
	}
	cout<<endl;
	
}
 
void DFT_test(){
	int N=64;
	vector<double> x_n(N);
	vector<complex_t> X_k(N);
	for(int i=0;i<N;++i){
		x_n[i]=i;
	}
	DFT(x_n,X_k);
	IDFT(X_k,x_n);
}
 
 
//保证N是2的n次幂
int bitlen(int N){
	int n=0;
	while((N&1)==0){
		n++;
		N>>=1;
	}
	return n;
}
 
 
int reverse_bit(int n,int len){//bit反转 
	int tmp=0;
	while(len--){
		tmp+=((n&1)<<len);
		n>>=1;
	}
	return tmp;
 
}
 
//序数重排 
void resort(vector<complex_t> &x_n,int N){
	vector<complex_t> v(x_n);
	int len=bitlen(N);
	for(int i=0;i<N;++i){
		x_n[i]=v[reverse_bit(i,len)];
	}
}
 
 
//基2,FFT算法实现,O(nlogn)的复杂度
void FFT(vector<complex_t> &x_n){
	int N=x_n.size();
	int r=bitlen(N);
	
	vector<complex_t> W(N);
 
	//预先计算旋转因子 
	for(int i=0;i<N;++i){
		double angle=-i*2*PI/N;
		W[i]=complex_t(cos(angle),sin(angle));
	}
	
	
	for(int k=0;k<r;++k){//迭代次数 
		for(int j=0;j<(1<<k);++j){
			int butterfly=1<<(r-k);
			int p=j*butterfly;
			int s=p+butterfly/2;
			for(int i=0;i<butterfly/2;++i){
				complex_t c=x_n[i+p]+x_n[i+s];
				x_n[i+s]=(x_n[i+p]-x_n[i+s])*W[i*(1<<k)];
				x_n[i+p]=c;
			}
		}
	}
	
	//次序重排 
	resort(x_n,N);
	int cnt=0;
	for(int i=0;i<N;++i){
		if(cnt==(int)sqrt(N)){
			cout<<endl;
			cnt=0;
		}
		++cnt;
		cout<<format(x_n[i])<<" ";
		
	}
	cout<<endl;
}
 
//IFFT,与FFT基本一致 
void IFFT(vector<complex_t> &x_n){
	int N=x_n.size();
	int r=bitlen(N);
	
	vector<complex_t> W(N);
 
	//预先计算旋转因子 
	for(int i=0;i<N;++i){
		double angle=i*2*PI/N;//IFFT的旋转因子与FFT的旋转因子差一个负号 
		W[i]=complex_t(cos(angle),sin(angle));
	}
	
	
	for(int k=0;k<r;++k){//迭代次数 
		for(int j=0;j<(1<<k);++j){
			int butterfly=1<<(r-k);
			int p=j*butterfly;
			int s=p+butterfly/2;
			for(int i=0;i<butterfly/2;++i){
				complex_t c=x_n[i+p]+x_n[i+s];
				x_n[i+s]=(x_n[i+p]-x_n[i+s])*W[i*(1<<k)];
				x_n[i+p]=c;
			}
		}
	}
	
	//次序重排 
	resort(x_n,N);
	int cnt=0;
	for(int i=0;i<N;++i){
		if(cnt==(int)sqrt(N)){
			cout<<endl;
			cnt=0;
		}
		++cnt;
		x_n[i]/=N;//IFFT与FFT还差一个系数 
		cout<<format(x_n[i])<<" ";
	}
	cout<<endl;
}
 
void FFT_test(){
	int N=64;
	vector<complex_t> x_n;
	complex_t c(0,0);
	for(int i=0;i<N;++i){
		c.real()=i;
		x_n.push_back(c);
	}
	
	FFT(x_n);
	IFFT(x_n);
}
 
 
int main(){
	DFT_test();
	cout<<endl;
	FFT_test();
	return 0;
}

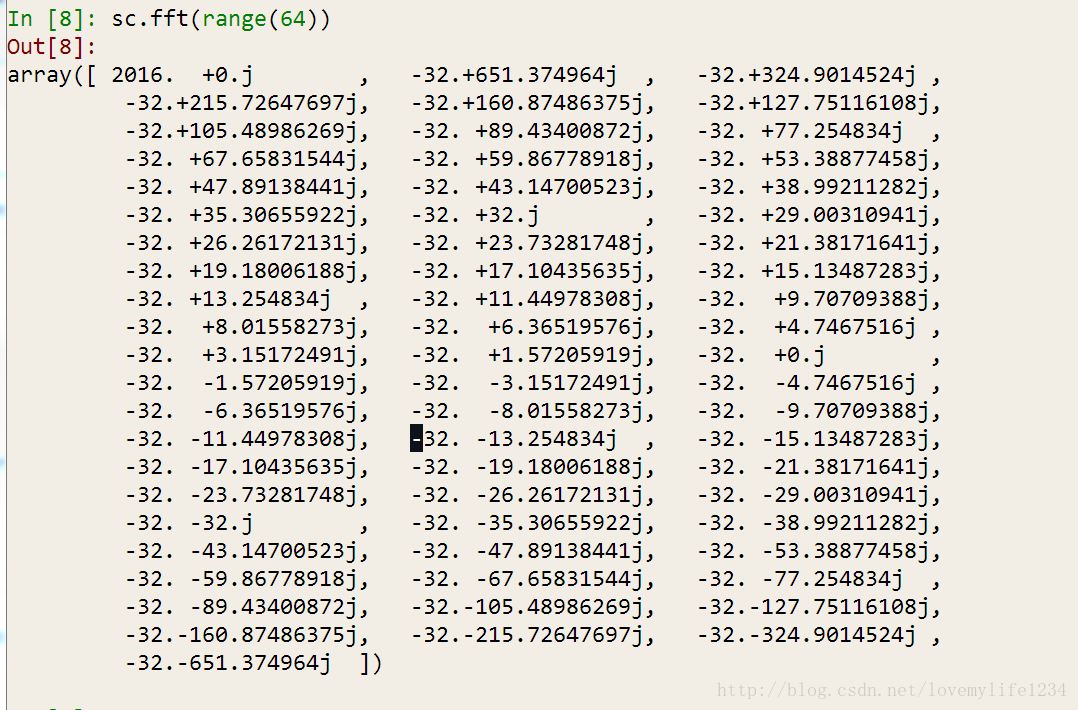
运行结果与Python的scipy库中的fft算法运行结果对比,基本验证了该算法的正确性: