计算机科学概论最近在学这个。费了大概一星期的课余时间来弄懂正负数、整数浮点、小数分数的互相转换。写出来,方便以后复习用。
基础篇:二进制简介
二进制转十进制:
与十进制的满十进一一样,二进制是满二进一的。所以用二进制表示的数与十进制存在如下关系(以8位为例)(为了便于排版,用了竖排):
1 -> 128 = 27
1 -> 64 = 26
1 -> 32 = 25
1 -> 16 = 24
1 -> 8 = 23
1 -> 4 = 22
1 -> 2 = 21
1 -> 1 = 20
往上,以此类推。因此,只要用2的n次方乘以对应位的数字就行。
举例:01001011(2)=0×27+1×26+0×25+0×24+1×23+0×22+1×21+1×20=75(10)
十进制转二进制:
- 这是我高中学的方法,也算是最笨的方法:使用短除法求余。将数值一直除以2,直到商为0。第一个取出来的余数是最靠近小数点的。
举例:125
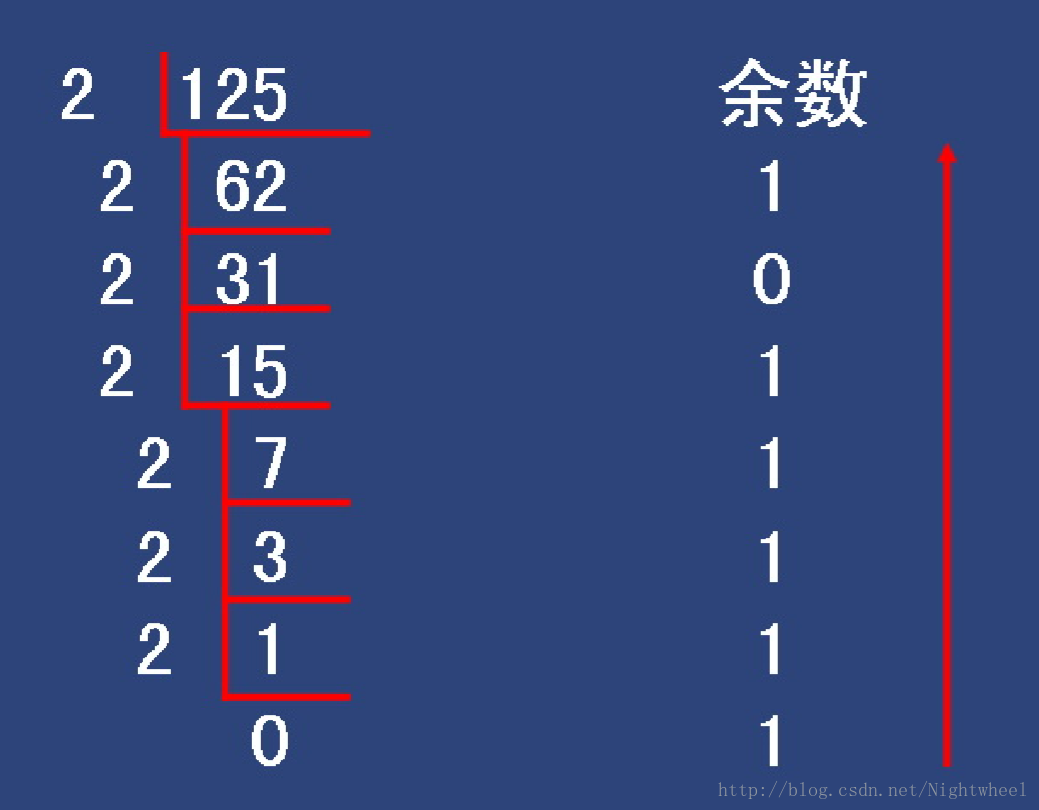
然后从下往上读,得到1111101。即125(10)=1111101(2)。 - 使用速算的方法。(大概是升级版?)
由二进制转十进制的方法可以推出该方法。记住低四位是8、4、2、1即可,其余的可以往上推出 举例:75 速算,得出75 = 64+16+4+1。与对应位的数字比较,得到75(10)=01001011(2)。
四则运算
二进制满二进一。因此以二进制进行四则运算时存在如下规律:
0+0=0, 0+1=1, 1+0=1, 1+1=10. 0×0=0,
0×1=0, 1×0=0, 1×1=1.
进阶篇:正负数、整数浮点、小数分数的转换
补码——正负数的转换
明确一点:负整数在计算机中是以二进制补码(two’ s complement)的形式储存的。为讲解方便,下面的位长度均为4.
在负数的储存中,最左边的一位是符号位,负数的符号位为0,正数的符号位为1。因此,在位长度为4的条件下,3(10)=0011(2),-3(10)=1101(2)。
-
十进制数求补码的方式
先将十进制数转换为二进制数,然后全部取反,最后将所得的数+1; 例:-6 写出6的二进制表示:0110; 全部取反:1001;
+1:1010 -
同样先写出二进制数,然后从右往左,将所有位的数字照抄下来,直到遇到第一个1为止,最后将这个1前所有位数取反。
例:-6
写出6的二进制表示:0110;
1前所有数字取反:10
合并:1010
推荐第一种方法,不容易算错。
二进制数转十进制数的方法:
先看符号位,0为正数,1为负数。如果符号位是0,直接转成十进制数;如果符号位为1,将所有位取反然后+1;或从右往左照抄所有数字,直到遇到第一个1,然后将1前所有位数取反,最后转成十进制数。
溢出
溢出(overflow)是指在算数计算中,得出的数值大于系统能表示的最大值或小于最小值的情况。溢出会造成错误,有可能给计算机造成损害。
举例说明。前面将位长度设为4,这样的话计算机只能储存从-8到7的整数。一旦我们计算的结果超过这个范围,就会引发错误。如6+4,你以为答案是10,但计算机给出的结果是-6。原因很简单,把6和4转成二进制再运算下:
0110+0100=1010=-6(10)
不过现在的计算机使用的位数比例子中的长得多,所以小数的运算大可不必担心。
移码
移码的计算方法很简单,将补码的符号位取反即可。
小数(浮点数)的转换
如无说明,位长度均为8位。
储存小数时,一般第1位为符号位;第2~4位为指数位(使用移码编码);第5~8位为尾数位。
十进制与二进制在小数点后的关系如下:
1 -> 1 = 20
1 -> 1/2 = 2-1
1 -> 1/4 = 2-2
1 -> 1/8 = 2-3
如此类推。
二进制转十进制
首先看符号位,0为正,1为负。接着看指数位,将指数位的数转为补码再判断正负、代表的十进制数是多少。最后看尾数位,按指数位的数字移动小数点(正往右,负往左),转成十进制数的最终结果。
例:01101011。
符号位为0,代表这个数是正数。指数位为110,转成补码为010,说明指数位的数字是2,之后处理小数点时要把小数点右移两位。尾数位的数为1011,依照指数位的数移动后,数字变为10.11,转成十进制为2 3/4。
例2:00111100
符号位为0,代表这个数是正数。指数位为011,转成补码为111,说明指数位的数字是-1,小数点要左移一位。尾数位的数为1100,小数点移动后数字变为0.0011,转成十进制为3/8。
十进制转二进制
先看符号位,0为正数,1为负数。接着将十进制数直接转成二进制数。再将小数点移动至所有数字前面,计算移动的位数和方向,然后转成补码,最后合并,得到结果。
截断
思考一下这个数字的转换:3 3/8。如果依旧用8位的位长度,转换成二进制后,这个数是这样的:01101101。
似乎哪里不对。再转回十进制看看。
尾数位是1101,小数点右移两位变为11.01,转成十进制是3 1/4。嗯?还有1/8去哪了?
这种位数丢失的情况就叫截断(truncation)。
还有一种情况。假设程序要储存1/3,而根据十进制与二进制的关系,计算机中只有1/2、1/4、1/8…因此计算机是不可能精确地储存这个数的,只能储存一个近似值。这也是截断错误的一种。
说好的方便复习,结果在期末考试前一晚才写出来……
有错请指出。
感谢观看。