这里写自定义目录标题

编译器
词法分析 Lexical Analysis
Syntax Analysis 语法分析
自顶向下分析 Top-Down Parsing
自底向上分析
语义分析 Semantic Analysis
中间代码生成 Intermediate code generation

这是上学期编译原理的归纳总结，为非正式版，函待完善

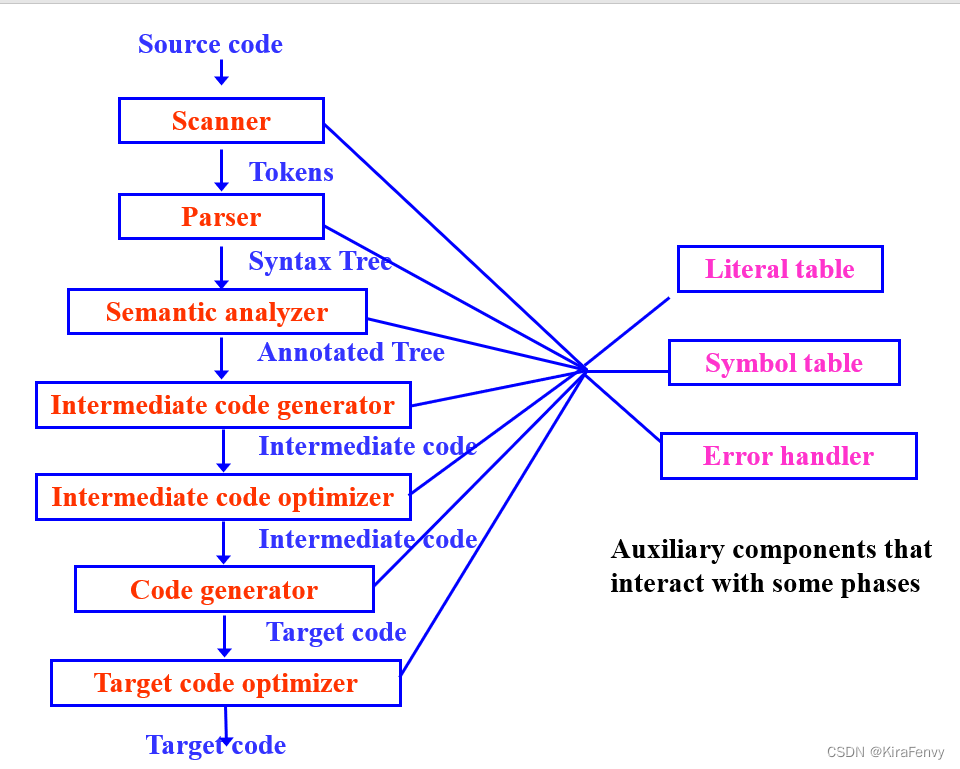
编译器

概念

编译器是将程序从一种语言翻译成另一种语言的计算机程序

Interpreter and Compiler 解释器和编译器

编译器工作流程

在这里插入图片描述

词法分析（扫描）：识别描述的逻辑片段。
语法分析（解析）：确定这些片段之间的相互关系。
语义分析：识别整体结构的含义。
中间代码生成：设计一种可能的结构。
中间代码优化：简化预期结构。
代码生成：制造结构。
优化：改进生成的结构。

词法分析 Lexical Analysis

将物理描述转换为tokens串（token为有意义的字符序列，Token 表示某种字符模式，例如标识符必须以字母开头，并且仅包含字母和数字）

扫描流程：

读取字符流
将字符分组到lexemes词素序列中。

Each token is associated with a lexeme.

Each token may have optional attributes.

在这里插入图片描述

选择有用的tokens：

为关键字提供自己的token。
为不同的标点符号punctuation symbols提供自己的token。
将表示标识符、数字常量numeric constants、字符串等的词素分组到自己的组中。
丢弃不相关的信息（空格、注释）

字母表，字符串和语言

Alphabet 字母表
- 符号的有限集合，如 ∑={0‚1} , Α={a‚b,c}
String 字符串
- 符号的有限序列，其中符号取自字母表
- 0,00,10 are strings of ∑={0‚1}
  a, ab, aaca are strings of Α={a‚b,c}
  空串 ε(叫做epsilon)
  {ε} 不等于空集
Language 语言
- 在某一个字母表上，字符串的任意集合，就是语言，空集和{ε} 也是Language

正则表达式 Regular Expressions

Regular expressions are a family of descriptions that can be used to capture certain languages (the regular languages). 正则表达式是可用于捕获某些语言（常规语言）的一系列描述。
Often provide a compact and human-readable description of the language. 通常提供紧凑且人类可读的语言描述。

Atomic Regular Expressions 原子正则表达式

符号ε是正则表达式，与空字符串匹配。
对于任何符号 a，符号 a 是仅匹配 a 的正则表达式。

Compound Regular Expressions 复合正则表达式

如果 R1 和 R2 是正则表达式，则 R1R2 是表示 R1 和 R2 语言的串联concatenation的正则表达式。
如果 R1 和 R2 是正则表达式，则 R1 |R2 是表示 R1 和 R2 并集union的正则表达式。
如果 R 是正则表达式，则 R* 是 R 的 Kleene 闭包的正则表达式。
如果 R 是正则表达式，则（R）是与 R 具有相同含义的正则表达式。

优先级：（R） > R* > R1R2 > R1 |R2
So ab*c|d is parsed as ((a(b*))c)|d

其他标志：
大括号：(0|1){4} 代表有四个0或1
问号：1*0?1* = 1*(0 | ε)1* 表示0个或1个
中括号：选择其中的一个数字或字母[A-Za-z] 一个任意字母，[0-9]一个任意数字
加号：表示1个或多个

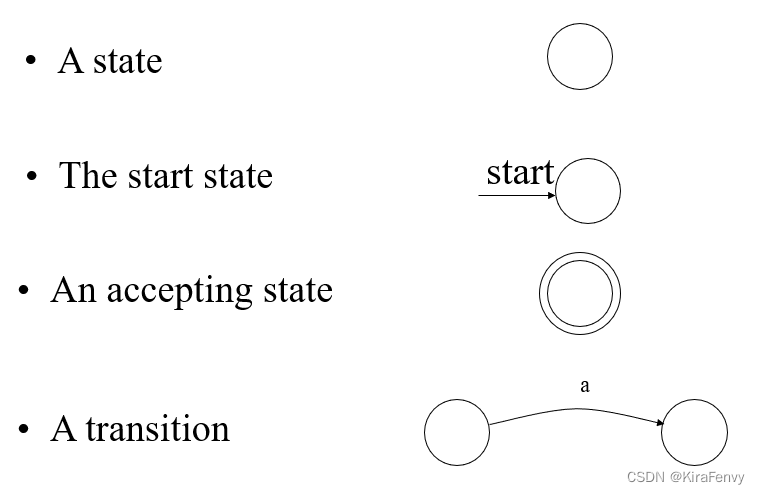
Finite Automata 有限自动机

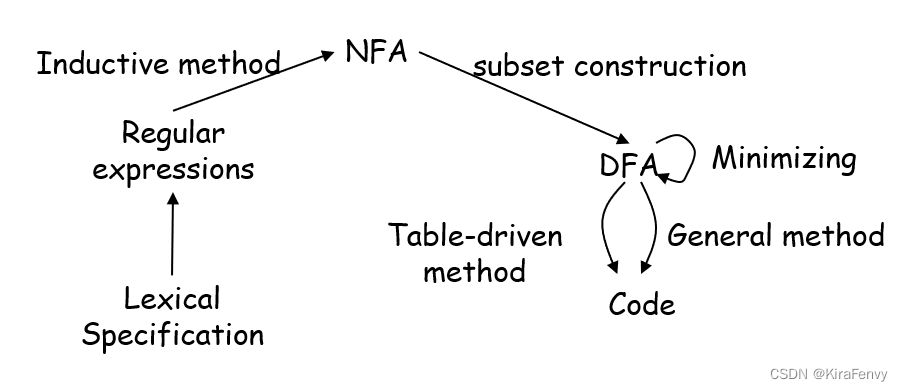
在这里插入图片描述

NFAs (nondeterministic finite automata),DFAs (deterministic finite automata),

有限自动机图示

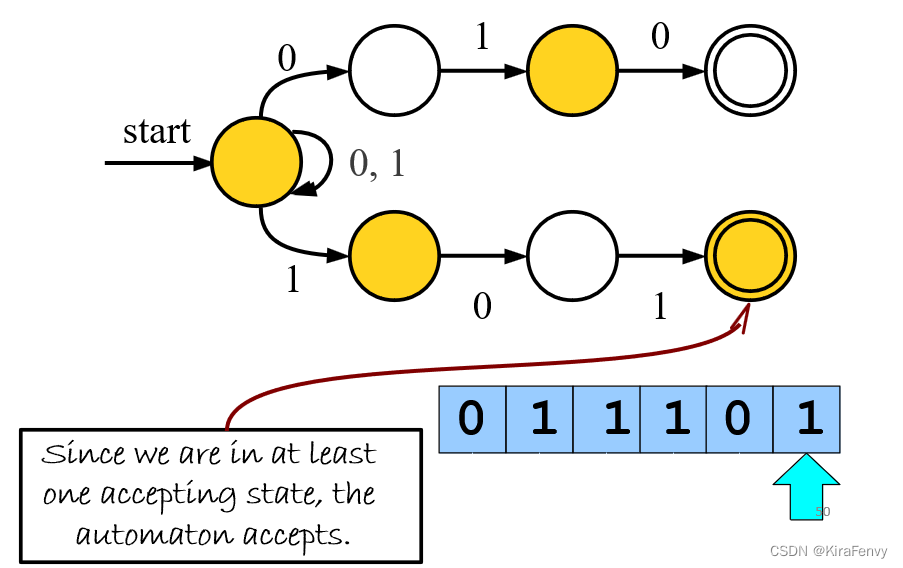
在这里插入图片描述
只要至少到一个接受状态，自动机就被接受（结束）

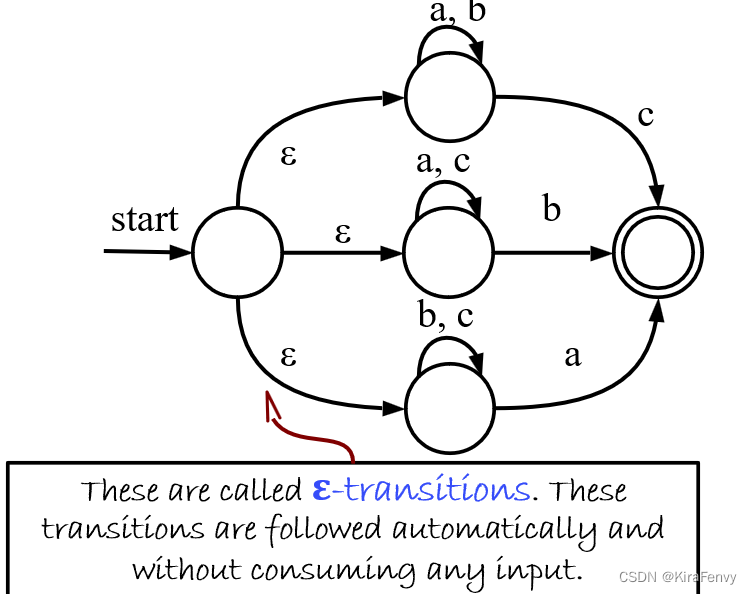
ε-transitions自动转换，不消耗输入！
在这里插入图片描述

NFA和DFA

Nondeterministic Finite Automata （NFA）：在给定状态下，一个输入可以有多个转换，可以有epsilon-transition
Deterministic Finite Automata（DFA）One transition per input per state 每个状态每个输入一个转换。不能有
epsilon-transition

模拟NFA：
跟踪一组当前状态，最初是开始状态以及ε移动可到达的所有内容。
对于输入中的每个字符：维护一组下一个状态，最初为空。
对于每个当前状态：遵循用当前字母标记的所有过渡，将这些状态添加到下一个状态集。将可通过ε移动到达的每个状态添加到下一个状态集。
复杂度：O（mn2） 表示长度为 m 的字符串和具有 n 个状态的自动机。

DFA：每个状态必须为每个字母定义一个转换，不允许ε移动。

DFA的两种表示方法

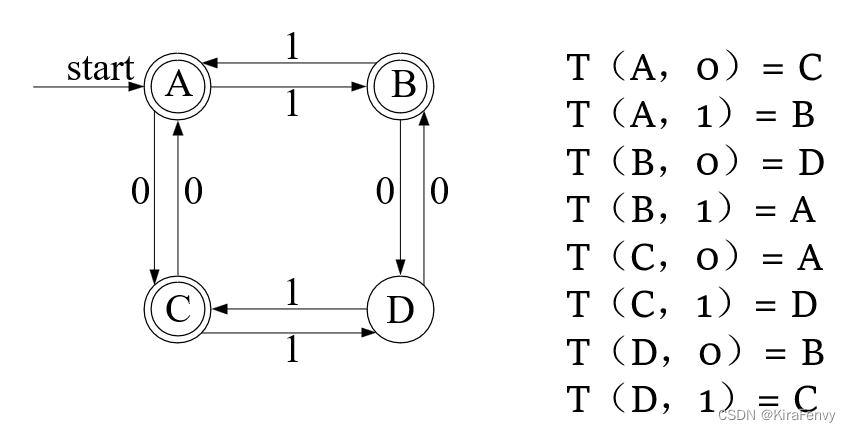
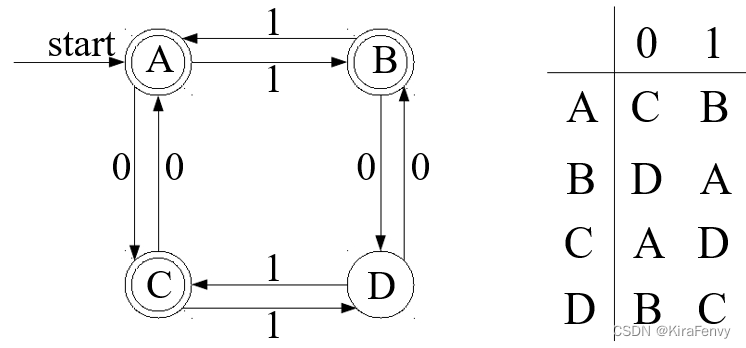
在这里插入图片描述

在这里插入图片描述
在字符串上运行DFA的时间复杂度O（n），n代表字符串的长度

正则表达式转换为NFA

目的是分解到每个箭头上面只有一个字符标记，转换流程：

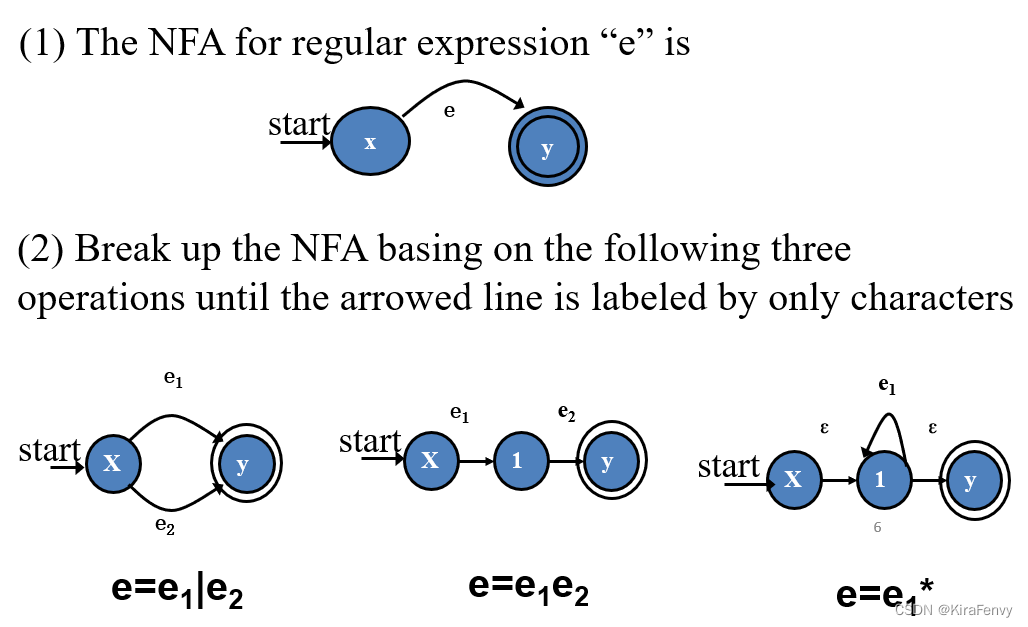
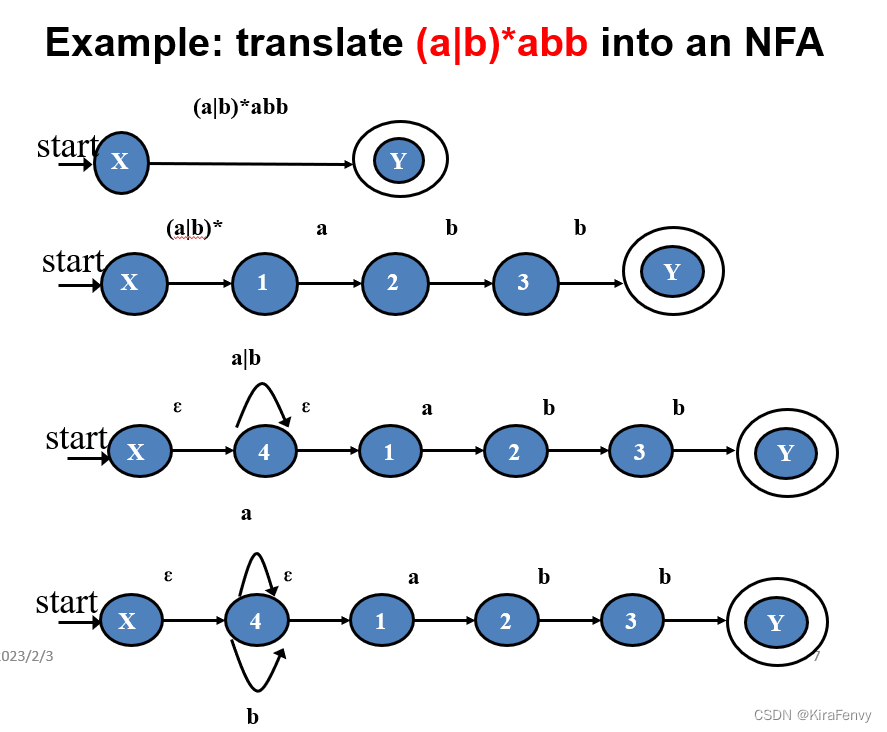
在这里插入图片描述

任何长度为 n 的正则表达式都可以转换为具有 O（n）状态的 NFA。
可以确定长度为 m 的字符串是否与时间 O（mn2）中长度为 n 的正则表达式匹配

NFA转化为DFA

我们如何确定哪些词素与每个标记token相关联？
当有多种方法可以扫描输入时，我们如何知道要选择哪一种？
解决方案是使用DFA scanner

回顾一下DFA的特性：

每个状态必须为每个字母定义一个转换。
不允许ε移动。

子集构造：
NFA 可以同时处于多个状态，而 DFA 一次只能处于一个状态。
关键思想：让DFA模拟NFA。
使 DFA 的状态对应于 NFA 的状态集。
DFA 状态之间的转换对应于 NFA 中状态集之间的转换。

转化步骤：
1.1. 消除ε-transition

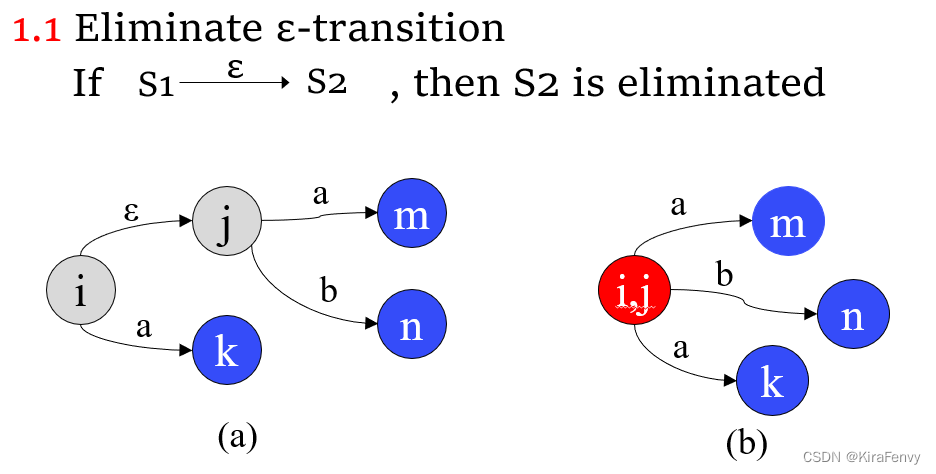
在这里插入图片描述
1.2 消除同一个状态出发的同一字符的转化

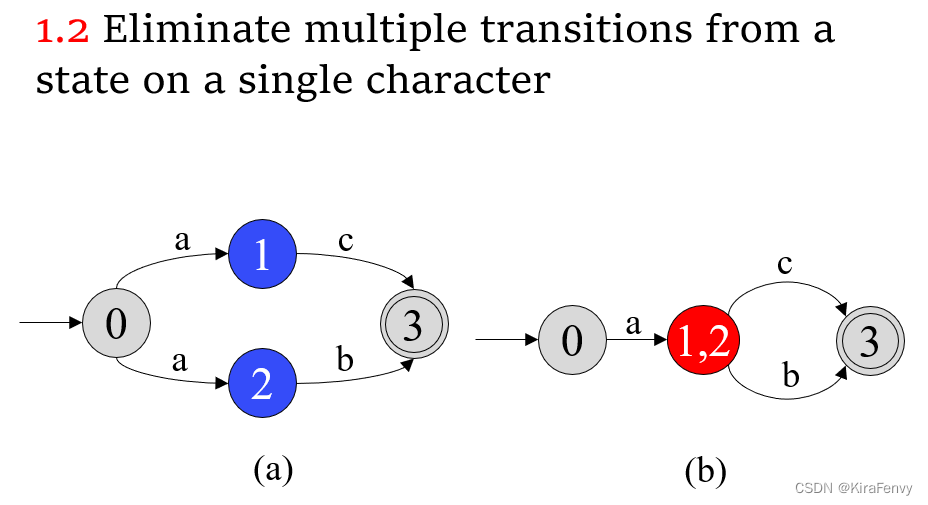
在这里插入图片描述
2.子集构造
使用 DFA 的一种状态来替换通过从单个输入字符上的状态转换而达到的 NFA 状态集

3.1 建立ε-closure 闭包
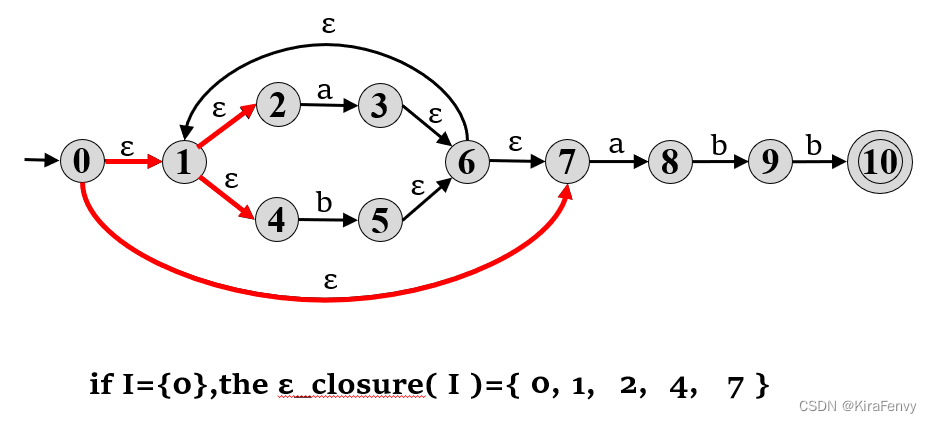
在这里插入图片描述

3.2

I_a

$I_{a}$ 子集
I 是一组状态，a 是字母表中的字符
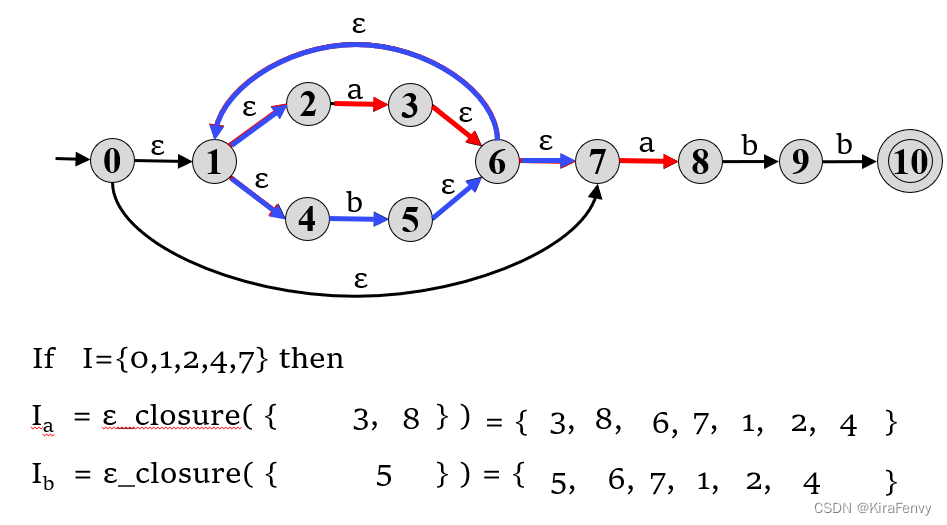
在这里插入图片描述

难以理解？看看例子：

I_a

$I_{a}$ 子集就是从a的下一状态开始找闭包，

I_b

$I_{b}$ 子集就是从b的下一状态开始找闭包
在这里插入图片描述

4.从给定的 NFA M 构造 DFA M’的算法

计算 M 的开始状态的ε_closure，这成为 M’ 的开始状态
对于这个集合，以及每个后续集合 S，我们计算每个字符 a∈Σ 上的转换 Sa，这定义了一个新的状态和一个新的转换
继续此过程，直到不创建新的状态或转换。
M’中那些包含接受状态 M 的状态标记为接受

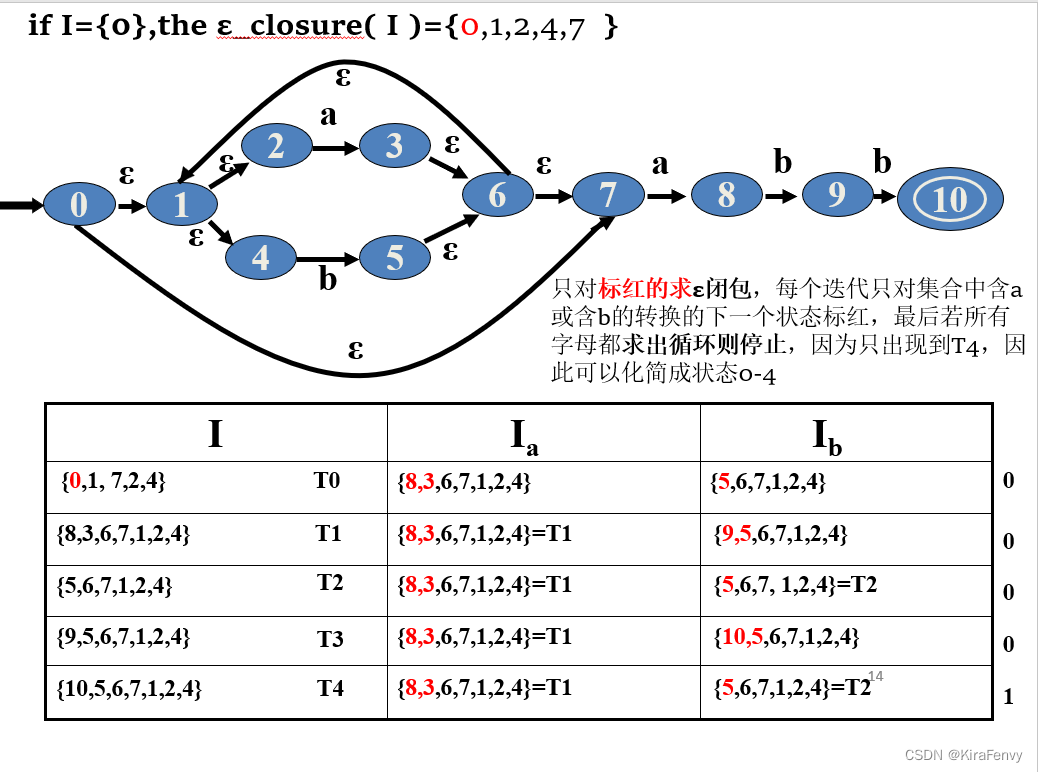
在这里插入图片描述
图中T4包含10接受状态，所以后面状态T4是接受状态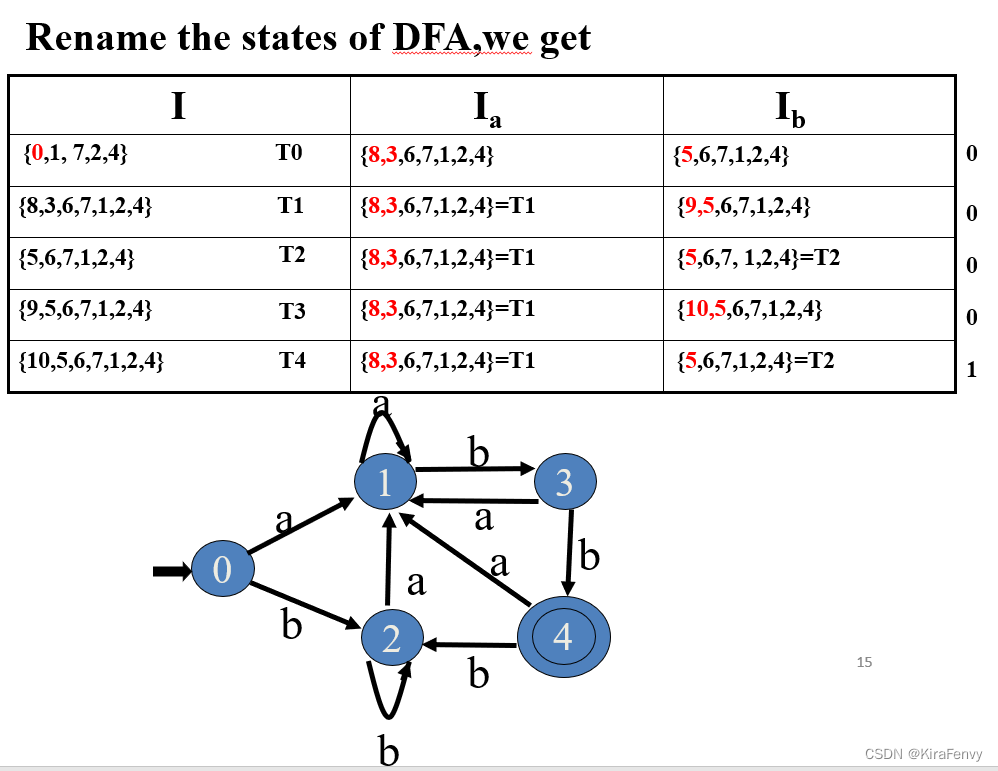

Minimizing DFA 最小化DFA

要把状态的数量最小化

它们都是正则表达式 a* 的 DFA，但后者是最小的

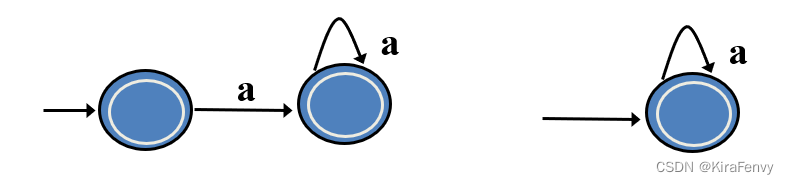
在这里插入图片描述

理论：给定任何 DFA，都有一个等效的 DFA，其中包含最小数量的状态，并且此最小状态 DFA 是唯一的

等效状态概念：
如果 s 和 t 是两个状态，则它们等价当且仅当：
– s和t都是可接受或者不可接受状态
– 对于每个字符a∈Σ（Σ代表字符表集合），s 和 t 在a上具有到等效状态的转换

例子：
C 和 F 都是接受状态。它们在“a”到 C 上有过渡，在“b”到 E 上有过渡，所以它们是等效状态
S 是不接受状态，C 是接受状态。它们不是等效状态
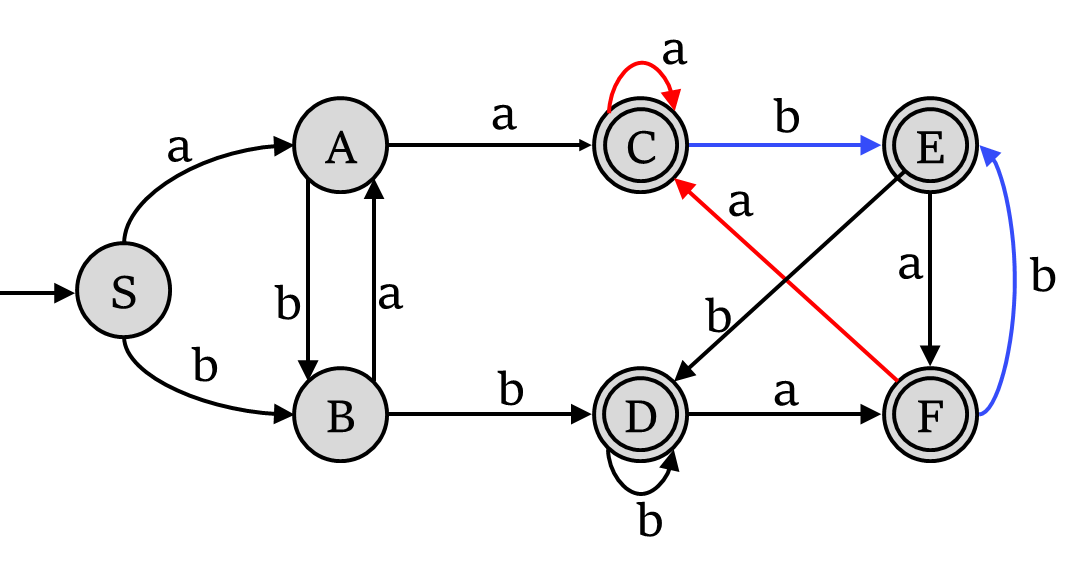
在这里插入图片描述
状态最小化算法
将状态集拆分为一些不相交的集合，因此一个集合中的状态彼此等效，而不同集合的任意两个状态是可区分的。

最小化的步骤：
1.将状态集分成两组，一组由所有接受状态组成，另一组由所有不接受状态组成。
2.考虑每个子集的字母表的每个字符“a”上的转换，确定子集中的所有状态是等效的还是应该拆分子集。
2.1 如果一个子集中有两个状态 s 和 t，它们在不同的集合中具有转化的 ‘a’ 上，我们说 ‘a’ 区分状态 s 和 t
2.2 所考虑的状态集必须根据其 a 转换所在的位置进行拆分
3. 继续此过程，直到所有集合都只包含一个元素（原始 DFA 最小）或直到不再发生集合的进一步拆分。

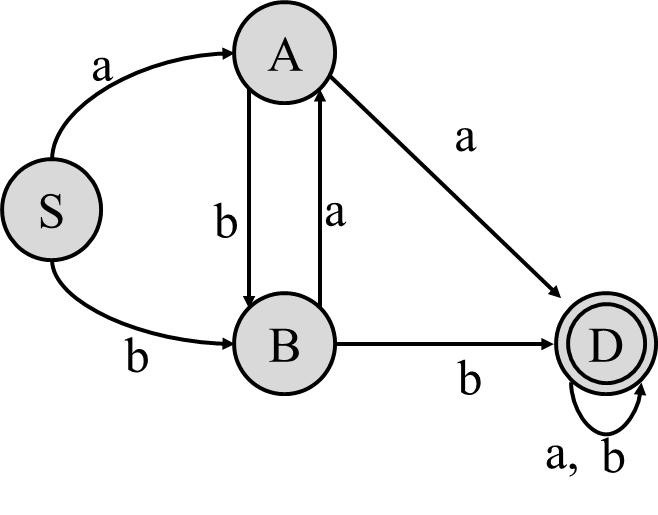
例子1：
将下图中的NFA转化为DFA
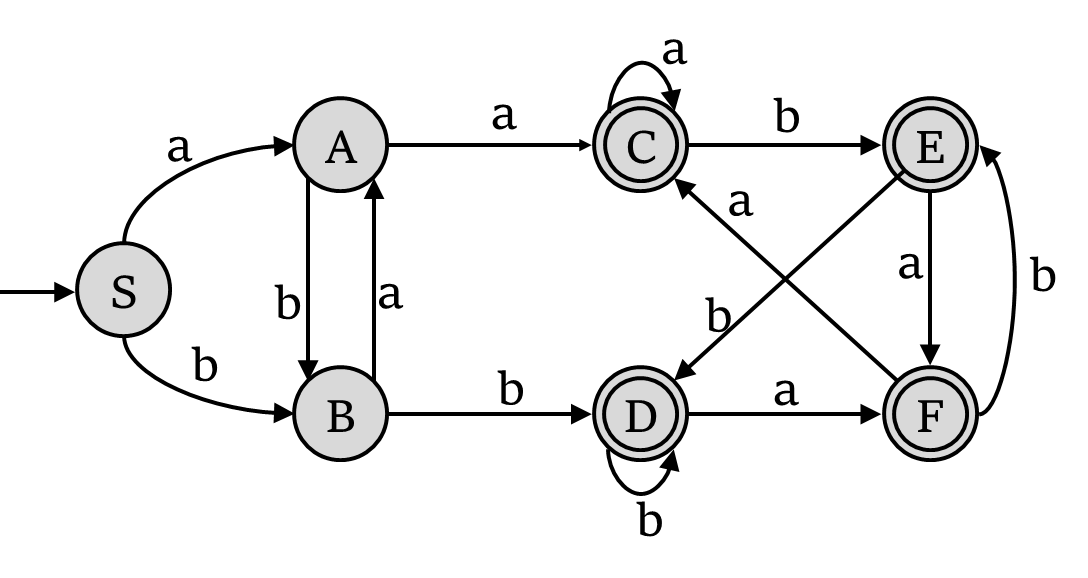
在这里插入图片描述

1.分为接受状态集和不接受状态集
{S，A，B}{C，D，E，F}
2 继续拆分
通过a拆分：{S，A，B}=>{S}{A}{B}
{C，D，E，F}
3 设 D 代表 {C，D，E，F}

可化成
在这里插入图片描述

例子2：
1）所有状态都是接受状态：{1，2，3}
2）没有一个状态用b来区分（3个状态经过b都到3），但a区分状态1与状态2和3：{1}{2，3}
3） {2，3} 不能用 a 或 b 来区分

Confliction Resolutions 冲突解决

如何确定词素和token的关联方式，当有多种方法可以扫描输入时，我们如何知道要选择哪一种？

Maximal munch 最长前缀匹配
priority system 优先级原则

假设所有标记都指定为正则表达式。
从左到右扫描，始终匹配其余文本的最长可能前缀（Maximal munch规则）

如何匹配Maximal munch最长前缀：
将表达式转换为 NFA。
并行运行所有 NFA，跟踪最后（最长）的匹配last match。
当所有自动机都卡住时，报告最后一个匹配并在该点重新开始搜索。

比如下列匹配，如double既满足do又满足double，取最长前缀
在这里插入图片描述

Syntax Analysis 语法分析

前面词法分析扫出token，而语法分析时可以分析恢复token结构

恢复一系列token描述的结构。
如果这些token未正确编码结构，则报告错误。

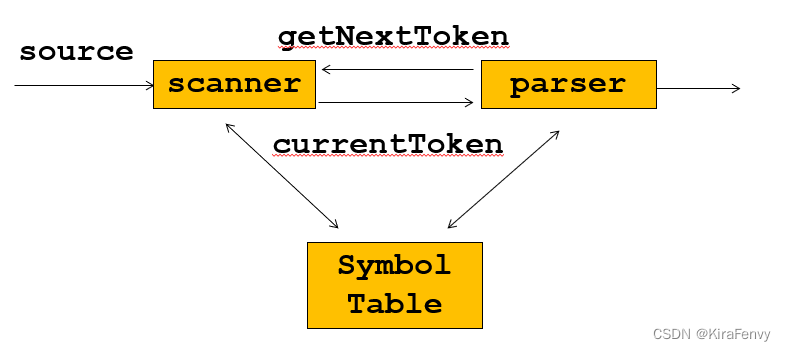
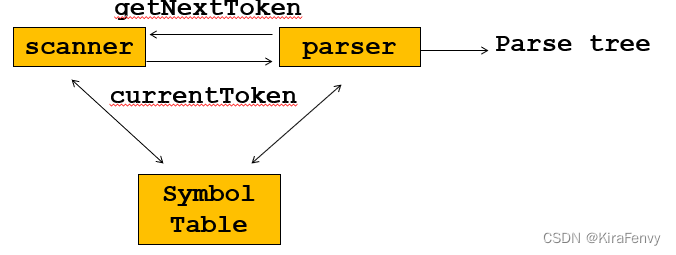
语法分析的输入输出：
输入：解析器调用扫描程序过程来获取下一个token
输出：需要构造显式或隐式语法树。语法树的每个节点都包含编译过程其余部分所需的属性
Scanner扫进token后给parser进行解析，如果解析正常就继续让scanner获取token

在这里插入图片描述

Context-Free Grammars 上下文无关文法

字母表是符号的集合∑，用作字母。

∑上的语言是一组由∑中的符号组成的字符串。

扫描时，我们的字母表是ASCII或Unicode字符。我们产生了token。

解析时，我们的字母表是scanner生成的一组tokens

正则表达式无法表达所有集合，如
在这里插入图片描述
这里没办法保证两边的a的数量相等

正则表达式表达能力不足：
无法定义与所有表达式匹配的正则表达式，并带有适当平衡的括号。
无法定义与具有正确嵌套块结构的所有函数匹配的正则表达式。

因此引入上下文无关文法，上下文无关语法（或CFG）是编程语言语法结构的规范。与正则表达式类似，不同之处在于上下文无关语法涉及递归规则（recursive rules），是正则语言的超集

例如算术表达式的上下文无关文法：
在这里插入图片描述
exp即expression的简写，op即operator的简写

定义

上下文无关的语法 G= （

V_T

$V_{T}$ ，

V_N

$V_{N}$ ， P， S）：

$V_T VT 是终结符集合。$
$V_N VN是一组非终结符集合， V N V_N VN∩ V T V_T VT=φ。$
P 是一组形式为 A→ α 的产生式或语法规则，其中 A∈ $V_N VN 和 α∈ （ V N V_N VN∪ V T V_T VT）$
S 是起始符号，S∈ $V_N VN$

解释：

$V_T VT 是构成字符串的基本符号。终结符是token$
$V_N VN 是表示字符串集的结构的名称$
以符号“S”表示的字符串集是由语法定义的语言
产生式定义一个结构，其名称位于箭头的左侧。结构的布局由箭头右侧定义
箭头的左侧不能简单地替换为其定义，因为定义的递归性质
X → Y1 …Yn 表示 X 可以替换为 Y1 …Yn
X → ε 表示 X 可以用空字符串替换

例子：
在这里插入图片描述
Notation Conventions 表示法约定：

一般第一个产生式的左侧是开始符号
使用小写字母表示终结符
使用大写字母或包含 <…> 的名称表示非终结符
如果 A→α1，A→α2,…,A→αn 都是左边带有 A 的产生式，我们可以写成 A→α1|α2|…|αn

注意符号不要与正则表达式混淆，应该进行改写，不能使用 *、|或括号。

改写1：
在这里插入图片描述
改写2：

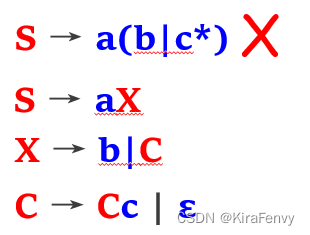
四种语法，不过只要掌握后面两个即可，越往下表示范围越小
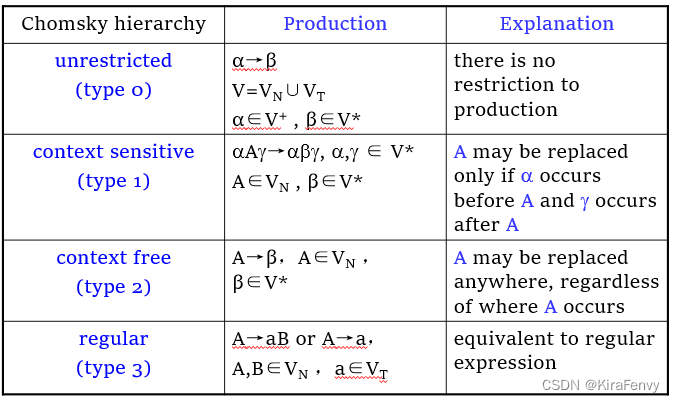
在这里插入图片描述

推导Derivation

推导的功能：
上下文无关语法规则确定一组语法合法的标记字符串
语法规则通过派生或归约来确定token的合法字符串
在这里插入图片描述

Derivation意味着用产生式右侧来替换非终结符

推导的例子：
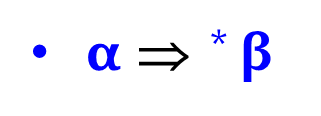
在这里插入图片描述

传递闭包

在这里插入图片描述

当且仅当存在 0 个或多个推导步骤序列（n>=0），
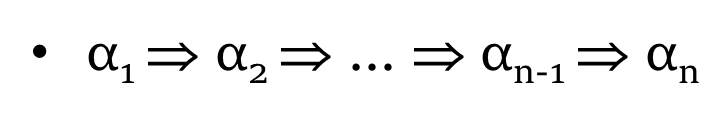
在这里插入图片描述

α= α1 且 β =αn. 如果 n=0, then α=β

设 G 是起始符号为 S 的上下文无关语法。那么G的语言是：

在这里插入图片描述
S 是 G 的起始符号，s 表示任意的标记符号字符串（有时称为句子）

Sentence句子

S 是 G 的起始符号，如果S传递闭包为α，α仅包含终结符和非终结符，则α是G的sentential form
若w是G的sentential form，且w仅包含终结符，则w是G的Sentence

例子：给定 G，L（G）可以通过推导获得
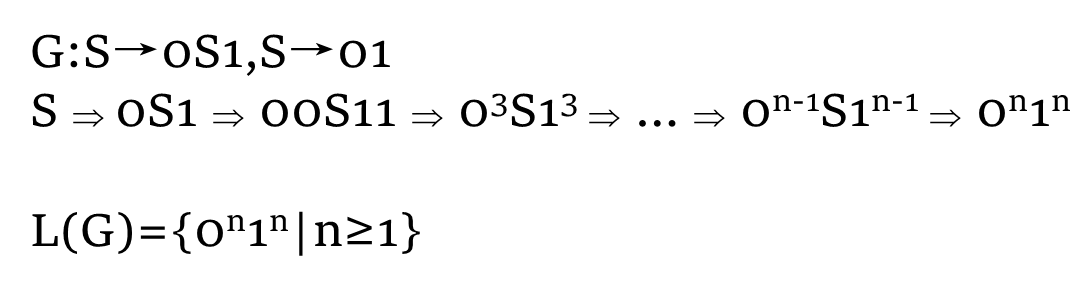
在这里插入图片描述
则S，0S1 ，00S11 ，000S111，00001111 都是 G 的sentential form
只有00001111是G的句子

例题：根据描述写出语法（产生式）
一种语言由 0 和 1 组成，该语言的每个字符串都有相同的 0 和 1 数
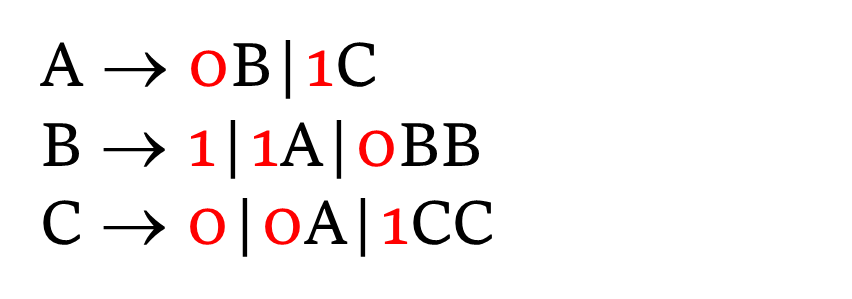
在这里插入图片描述

Parse Trees语法分析树

定义：
解析树是token字符串结构的有用表示形式
解析树直观地表示派生

语法分析树的组成部分：

根节点是开始符号
叶子结点是终结符或者ε
非叶子节点是非终结符
如果标签为 A ∈ $V_N VN 的节点有 n 个标签为 X1，X2,…,Xn（可能是终端或非终端）的子节点，则A → X1X2…Xn ∈P$

派生可以表示为解析树
对于产生式 X→Y1 …Yn 添加子项 Y1， …， Yn 到节点 X

推导和语法分析树：
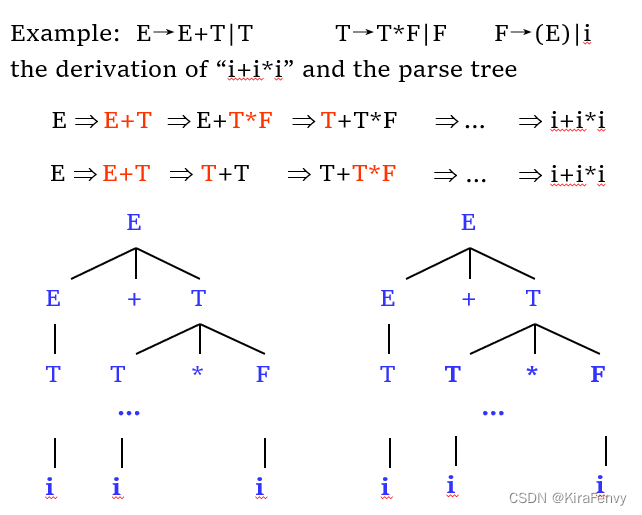
在这里插入图片描述
派生不唯一地表示它们构造的字符串的结构，而解析树可以

最左推导 LeftMost Derivation

在推导的每个步骤中替换最左边的非终结符的推导，相当于前序遍历

示例：
在这里插入图片描述

最右推导

在推导的每个步骤中替换最右边的非终结符的推导它对应于解析树的后序遍历的反向

在这里插入图片描述

抽象语法树 Abstract Syntax Trees（AST）

解析树包含的信息比编译器生成可执行代码绝对必要的信息多得多，抽象语法树仅包含真正需要的信息
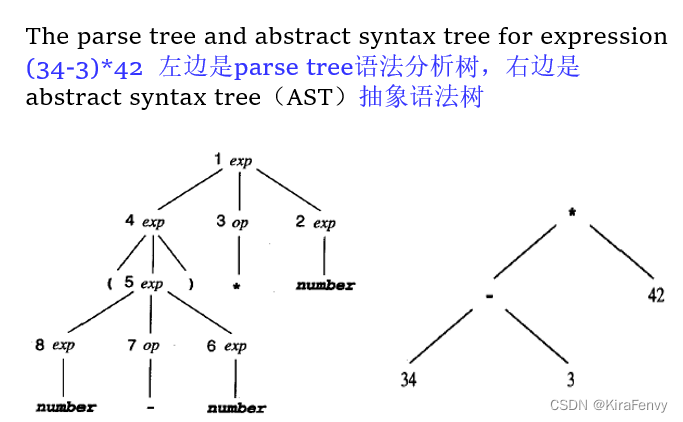
在这里插入图片描述
区别：AST的运算符在中间节点而不是叶子结点
AST 是用于后续编译阶段的更好结构
抽象语法树表示实际源代码标记序列的抽象
parser将遍历解析树表示的所有步骤，但通常只会构造抽象语法树

字符串的语法分析树和抽象语法树：
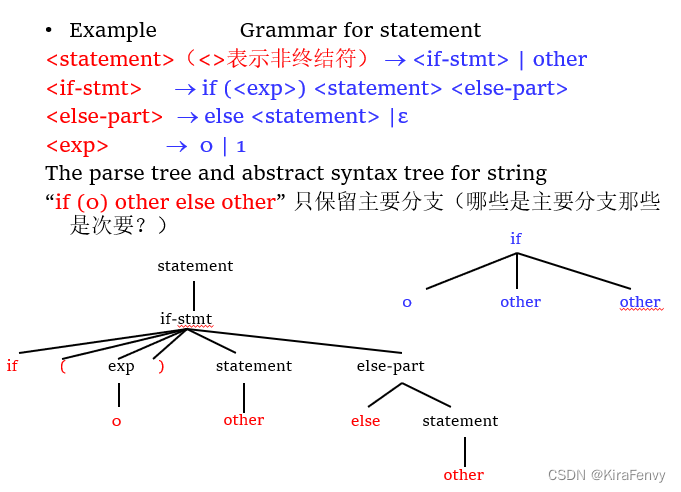
在这里插入图片描述

二义性ambiguity

可能一个表达式的最左最右推导的解析数是不同的，有二义性ambiguity

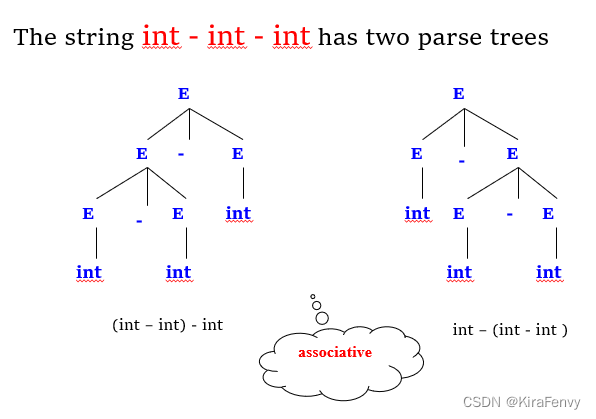
在这里插入图片描述
因此需要消除二义性规则（乘法优先，减法左结合）

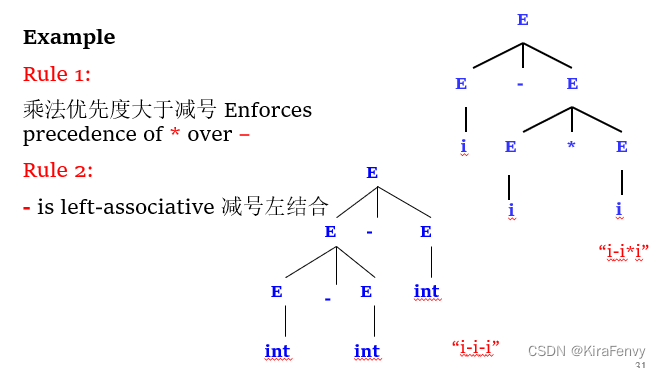
或者重写语法，将运算符分组为优先级相等的组，对于每个优先级，我们必须编写不同的规则。
在这里插入图片描述

将语法更改为强制构造正确解析树的形式（考试考的少）
考试主要考判断是否具有二义性并给出理由（画语法树）

小结：
语法分析（解析）从扫描程序生成的token中提取结构。
语言通常由上下文无关语法（CFG）指定。
语法分析树显示如何从语法派生字符串。
如果字符串具有多个分析树，则语法不明确。
抽象语法树 （AST）包含程序语法的抽象表示形式。

自顶向下分析 Top-Down Parsing

parsing语法分析的目标：恢复程序的语法结构

自顶向下就是从开始符号开始推导，过程大约如下：
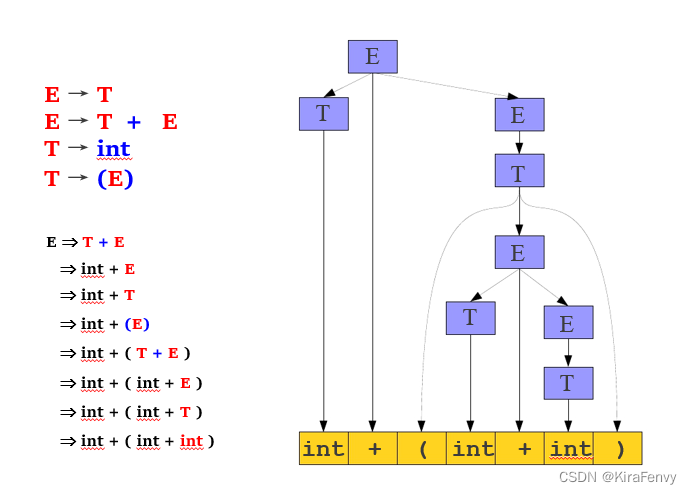
在这里插入图片描述

最终要推导出的是终结符

在这里插入图片描述

但是有多个产生式多个推导时如何选择？因此要进行Predictive parsing预测解析
两种预测解析的方法：
Recursive-descent parsing 递归下降分析
LL(1) parsing

输入字符串的分析以语法的开始符号开头
如果它可以根据输入中的前瞻token唯一地确定下一个在推导中使用哪个产生式，则解析是预测性的
Predictive parsers接受 LL（k）语法

L means “left-to-right” scan of input从左到右扫描
L means “leftmost derivation”最左推导
k means “need <= k tokens of lookahead to predict”需要预读k个词法单元分析预测（k大代价大）

First集

定义
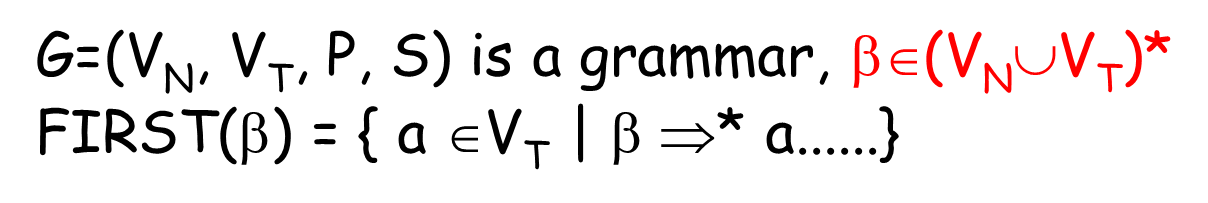
在这里插入图片描述
β可以推导出的所有token当中的首终结符集合，

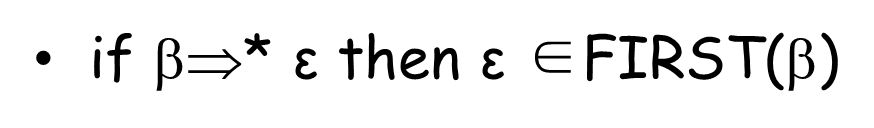
在这里插入图片描述
如果β是ε的传递闭包，则ε也在β的First集当中
.
简单说就是β的产生式右边的第一个终结符就是First集属性

在这里插入图片描述

Follow集

在这里插入图片描述
简单来说，非终结符A的Follow集就是产生式右边跟在A后面的终结符，如果有产生式后面什么都不跟那么$也在Follow集中

例子：
在这里插入图片描述

Let the current input symbol is “x” 不同情况选择不同的产生式
如果 x ∈FIRST（bAS）={b} ，则选择 A→bAS 进行派生
如果 x ∈FOLLOW（A）={$，a，d } ，则选择 A→ε 进行派生
因为 FIRST（bAS）∩FOLLOW（A）= Φ ，所以可以选择产生式，下面有个规则

LL（1）文法

LL（1）文法定义

判断是否为LL（1）文法的两个条件

For each production A → α1|α2|…|αn , for all i and j, 1≤i, j ≤ n, i≠j , First(αi) ∩First(αj) = Φ
- 所有同一符号推出的产生式的右部的First集的元素不重复
For each nonterminal A such that First(A) contains ε, First(A) ∩Follow(A) = Φ
- 对于First集包含ε的所有非终结符，则需要First集和Follow集的交集为空

例子：判断下列产生式是否符合LL（1）文法
在这里插入图片描述
因为First（A）∩Follow（A）={b}≠Φ，
故G[S] 不是 LL（1）语法，当最左边要替换的非终端是 A 并且当前输入符号是 “b” 时，解析无法确定选择 A 的哪些产生式：A→bA 或 A→ε

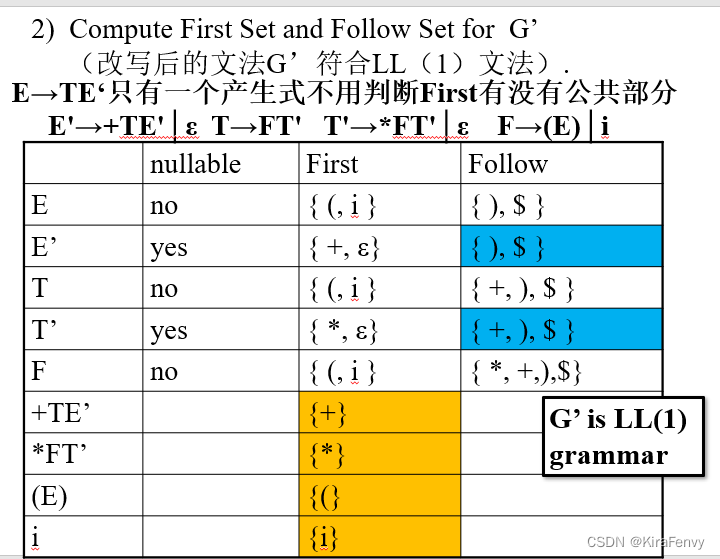
判定LL（1）文法方法(重点）

a) 计算可空非终结符集合
b）为每个产生式的右侧字符串α计算 FIRST(α)集
c）计算每个非终端 A 的Follow(A)
d）根据LL（1）的定义进行识别

可空非终结符集合的计算

存在一个推导使非终结符A的传递闭包为ε 就证明可空

若U 表示可空的非终结符集合

step 1: U={ Aj | Aj→ ε 是一个产生式} 即将每个直接推出ε的非终结符加入集合当中
step 2: 对每个产生式 p: Ap→X1…Xn, if X1…Xn∈U, then U:= U∪ {Ap }
- 当 $A_p Ap推出来的非终结符全是之前在可空集合里面的非终结符（必须X1到Xn都在集合内），则 A p A_p Ap加入集合U中$
step 3: 重复第二步直到集合U不变

例子：
在这里插入图片描述

计算First集

First集计算分成计算每个符号的First集和计算串的First集两种，这里先介绍计算每个符号的First集合

step1：对终结符，First集就是本身
step2：对非终结符，看传递闭包，传递闭包为ε则First集为ε，否则传递闭包为空
step3 对于在产生式左侧的非终结符，见SecondFirst描述
重复step3直到集合不变

在这里插入图片描述

在这里插入图片描述
步骤：

if X1 is not nullable, then SectionFirst(X1…Xj…Xn) =First(X1) 第一个符号不可空时，所有推出的子串的Fitst集就是X1的first集
if X1 is nullable, then SectionFirst(X1…Xj…Xn) =First(X1) -{ε}, and continue to see X2. Stop until Xi is not nullable . 若X1可空，就一直往后找，直到有不可空的
if X1…Xn are all nullable, then SectionFirst(X1…Xn)= (First(X1) -{ε}) ∪(First(X2)-{ε})∪… ∪(First(Xn) -{ε}) ∪{ε} 若一直找不到可空的，就把ε加进First集中

例子：

例1：
在这里插入图片描述
这里关注S和C的First集，S推导出AB，而A,B均可空，因此A，B的First本身含的a,b然后再把ε都加进First(S)，C推导出AD，A可空而D不可空，把AD含的a,b,c加进First( C )

计算产生式右侧的First集

假设α=X1X2…Xn，要计算First(α)

若X1不可空，则直接等于X1的非终结符
若X1可空，就一直往后找，直到有不可空的
若找到后面都可空，则First集为所有符号的First集加上ε

例2：这里计算的是产生式右侧的First集
在这里插入图片描述

计算每个非终结符的Follow集

step1：S 是起始符号，Follow（S）={$};对于所有非终结符A，和 A≠S，Follow（A）={ };
step2：对于每个产生式 B→αAγ，对于每个非终结符A：
- Follow(A)=Follow(A) ∪ (First(γ) -{ε})，即在A后面的符号的First集减掉ε
- if ε ∈ First(γ) then add Follow(B) to Follow(A) 如果非终结符后面的符号First集包含ε，就要加Follow(B) to Follow(A)
step3：重复step2直到follow集合不变

例子：求每个非终结符的Follow集，首先要求出每个符号的First集
这里的G（S）证明S是起始符号，一定有$
另外产生式右侧非终结符后面没符号也加上$
在这里插入图片描述

注意事项：

空串ε可以出现在First集但不能出现在Follow集
Follow集只是为了非终结符定义的，即Follow（X）中的X只能是非终结符

通过LL(1)文法定义来识别LL（1）文法

在这里插入图片描述
例子：判断G[S]是否为LL（1）文法

将非LL（1）文法转化为LL（1）文法

消除left factor左公因子和左递归是LL（1）文法的必要不充分条件

左公因子

同一个非终结符推出的，具有公共前缀，这个公共前缀就是左公因子，有这个左公因子就不是LL（1）
在这里插入图片描述

左递归

从A开始推导又推出A开头的符号串，则为左递归

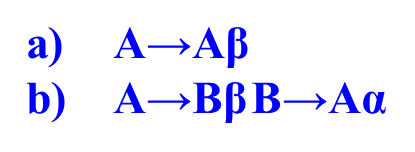
在这里插入图片描述
这里a式子是immediate left recursion立即左递归，b式子是indirect left recursion间接左递归，推好几次才回到A开头

判断左递归的方法

对于下面的两个左边相同的产生式
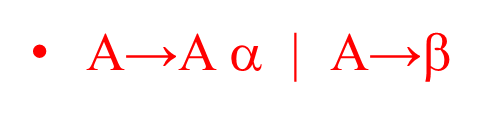
在这里插入图片描述
一个产生式右边的First集包含另一个产生式右边的First集，就是左递归的，这里First(Aα)包含First(β)，当然直接以A开头的立即左递归本身就很明显

不能保证消除左递归和消除左公因子这些技术的应用会将语法转换为LL（1）语法，转换之后要使用上节手段进行判断

消除左递归 Left Recursion Removal

消除的方法：
把
A→Aα1|Aα2|…|Aαm|β1|β2|…|βn
改成
A→β1A’|β2A’|…|βnA’
A’→α1 A’|α2 A’|…|αm A’|ε
即把左递归变成右递归，但要加上ε
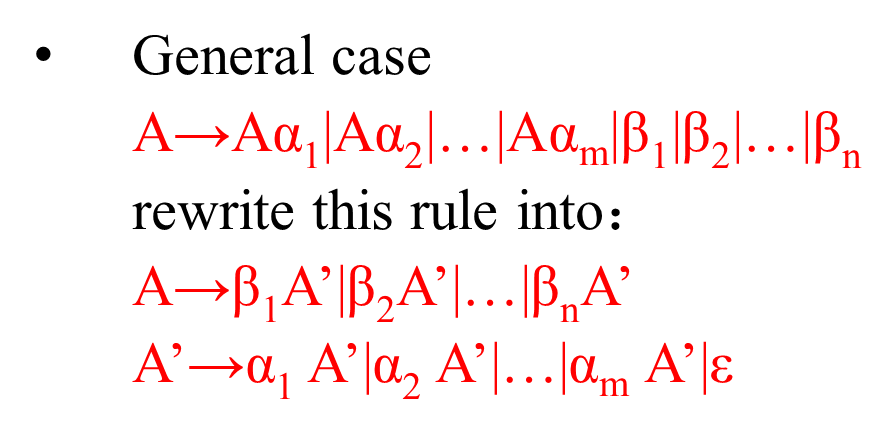
在这里插入图片描述

简单例子：
A → Aα| β 改写成
A → βA’, A’ → αA’| ε

复杂例子：
这里E和T都有能看出来的直接左递归
在这里插入图片描述

消除左公因子 Left Factoring

这个比较简单，提公因子就是了

在这里插入图片描述

递归下降分析 Recursive-Descent Parsing

为每个将识别 A 的非终结符A 定义一个过程
A 的语法规则的右侧指定此过程 A 的代码结构
- 终结符对应于输入的匹配
- 非终结符对应于对其他过程的调用
- 选项对应于代码中的备选项（大小写或 if 语句）

构造递归下降分析的过程

1. 消除G的左递归或左公因式成为G’

在这里插入图片描述

2. 判断G’是否符合LL（1）文法

在这里插入图片描述

3. 构造G’的递归下降分析

由一个主过程和一组递归过程组成，每个过程对应于语法的非终结符
使用的变量：

token是一个变量，用于在输入中保留当前的下一个token
match(y)是下一个令牌 TOKEN 与其参数 y 匹配的过程，如果成功，则推进输入，如果不成功，则声明错误
error是打印错误消息并退出的过程

3.1 “或运算”|的递归下降代码
对于非终结符U，如果U → x1 | x2 |…|xn, and x1,…,xn≠ ε，则过程U的代码：

if TOKEN in First(x1) then p_x1
      else if TOKEN in First(x2) then p_x2
              else …
              ….
                   else if TOKEN in First(xn) then p_xn
                       else ERROR

如果产生式包含U → ε
则要把

if TOKEN in First(xn) then p_xn 
	else ERROR

改写为

if TOKEN in First(xn) then p_xn
     	else if TOKEN not in Follow(U) then ERROR

3.2 “与”运算的递归下降代码
x=y1y2…yn的代码

begin p_y1;p_y2;…;p_yn end

如果 yi∈VN （非终结符）则p_yi是过程 yi 的调用;否则，如果 yi∈VT（终结符）则p_yi是match（yi）

例：
E→TE ’ E’→+TE’│ε
T→FT ’ T’→*FT’│ε
F→(E)│i
1）调用开始符号E的main函数

(1)  program  MAIN;                             	/* main */
       begin
          GETNEXT (TOKEN);
          E ;                           			/* call E */
          if  TOKEN ≠‘$'  then  ERROR
      end.

2）E→TE ‘的递归下降

(2)  procedure  E;             			/*E→TE'*/
      begin
         T;                             	 		/*call T*/
         E’ 						/*call E’*/
     end

（3）E’→+TE’│ε
这里注意要算E’的Follow集

(3)  procedure  E’;          		/*E'→+TE'│ε*/
       begin
          if  TOKEN=’+’  then         	/*E'→+TE'*/
             begin
                match(‘+’);（match表示当前必须匹配加号，否则不符合语法规则）	
                T;                     		/*call T*/
                E’ 	 			/*call E’*/
             end					
         else                                   /*E’ → ε*/
		if  TOKEN≠’)’ and TOKEN≠’$’  then  ERROR  
	  end;

4） F→(E)│i

(4)  procedure  F;      		            /* F→(E)│i */
       begin
          if  TOKEN = '('  then           /*F→(E) */
              begin
                 match(‘(’); 
                 E;                         	 /* call E */   
                 match(‘)’)
              end
          else 				/* F→i  */
		 	if  TOKEN=‘i’  then match(‘i’)
			else error;
	   end;

3.3 大括号（表示重复的，与while关联）
递归可以这样改写
在这里插入图片描述

E→ T {+ T} 
(1)  procedure  E;
       begin
		T;
		while token=‘+’ do
			match(‘+’);
			T;
		end while;
	   end

3.4 [ ] 中括号表示可选的，出现0次或1次
Example:

	if-stmt->if (exp) stmt 
			| if (exp) stmt else stmt
	
改写成
	if-stmt->if (exp) stmt [else stmt]

例子：

if-stmt → if (Exp) Stmt [else Stmt]
翻译成递归下降代码
	Procedure ifStmt;
	begin
		match(‘if’);
		match(‘(‘);
		Exp;
		match(‘)’);
		Stmt;
		if token=‘else’ then  //识别分支
			match(‘else’);
			Stmt;
		end if;
	end ifStmt;

LL（1）分析 LL(1) parsing

Predictive Parsing的方法一种是递归下降分析，一种是LL（1）分析

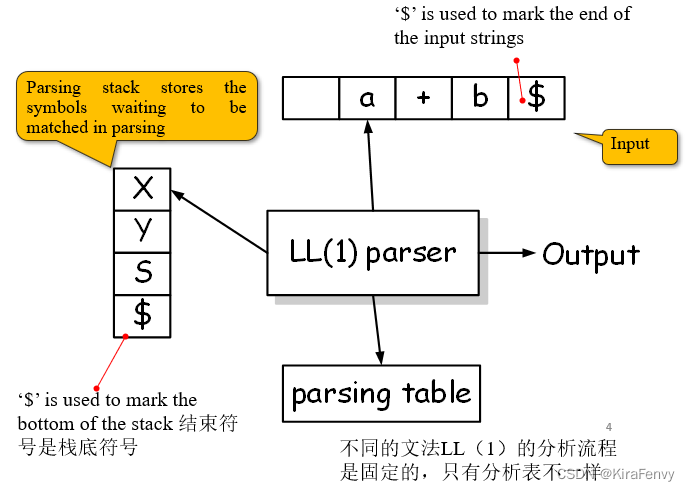
在这里插入图片描述

LL（1）分析流程

将开始符号放到栈中
如果栈顶是终结符，就执行match，看栈顶和当前输入是否相同
栈顶是非终结符，替换。对于A → α产生式，先把A弹出去，然后反向把α压进去（比如α 代表b+c，先把c压进去）
栈顶和输入串同时到结束标记$时，停止

例子：
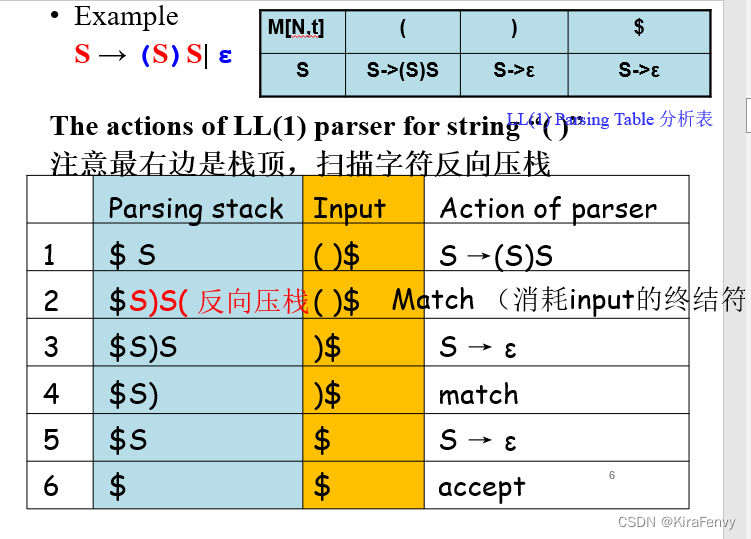
在这里插入图片描述

LL（1）分析表

作用是决定可以用哪个产生式替换非终结符
是个二维数组（二维表格），每一行一个终结符，每一列一个非终结符
如果 M[N，t] 在构造后保持为空，则表示解析过程中可能发生的潜在错误

构造LL（1）分析表

对每个非终结符 A 和产生式 A → α 重复以下两个步骤：

对First(α)集里面每一个token，把产生式填进去（A直接推出）

若A的First集包含空串ε，进行第二步
如果ε在First(α)中，对Follow（A）的每个终结符’a’对应的产生式加进去（a可以出现在A后面，让A消失后面的a推出）

例子：要构造左边的语法的LL（1）分析表
（1）清除左递归，清除左公因子
在这里插入图片描述
（2）计算出所有非终结符的First集合Follow集合

（3）根据前面所述构造分析表
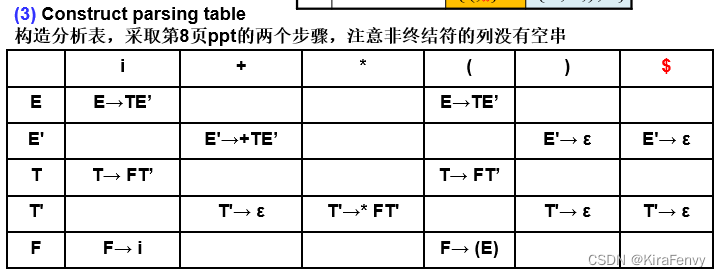
在这里插入图片描述

如果关联的 LL（1）分析表在每个表条目（每个单元格）中最多有一个产生式，则语法就是 LL（1）语法。

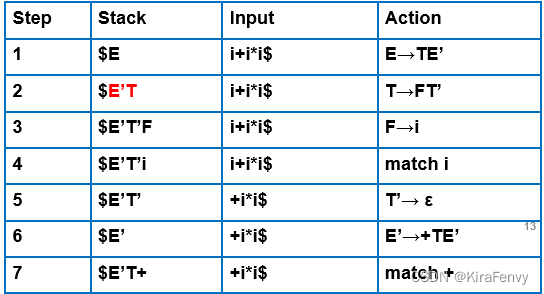
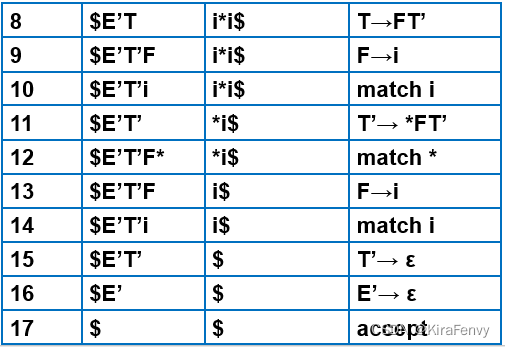
若用该分析表对某个串进行分析，过程如下：

在这里插入图片描述

自底向上分析

自底向上分析概述

主要思想

定义：从输入串开始，通过归约（反向利用产生式）最后把token串归约为开始符号
输入字符串是语法分析树的叶子，从这开始到开始符号（根节点）
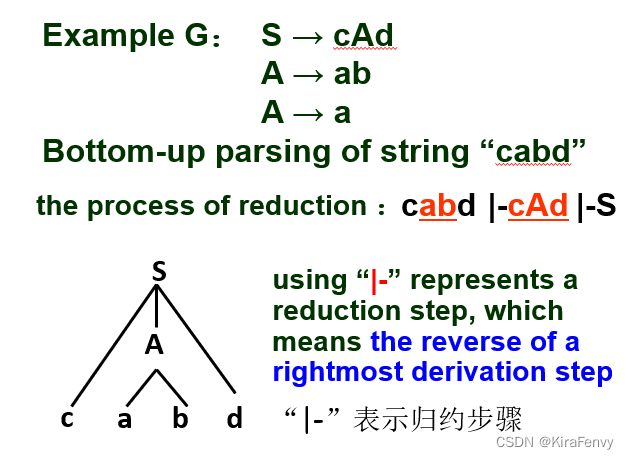
在这里插入图片描述

但重点是确定要使用哪个字符串和产生式归约，比如
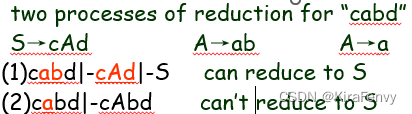
在这里插入图片描述
是两种不同的归约，一种可以到S一种不可以

自底向上分析的实现

采用Parsing Stack分析栈，自下而上的解析器使用显式堆栈来执行解析
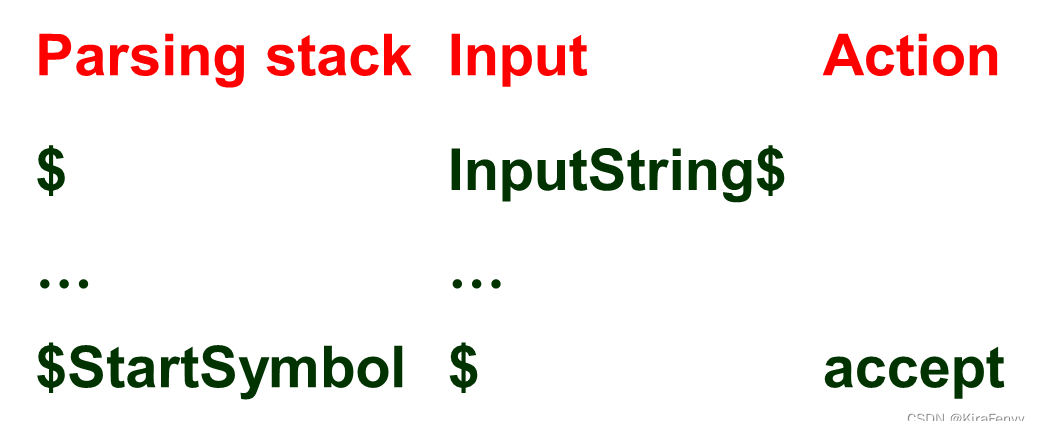
在这里插入图片描述

栈中包含token、非终结符和状态（比自顶向下的多了个状态）
自上而下的解析堆栈存储等待在parsing中匹配的符号，而自下而上的解析堆栈存储已匹配的符号

自底向上的两种操作：

Shift: shift a terminal from the front of the input to the top of the stack 移入：将左边的token从输入串移动到栈顶
Reduce: reduce a substring α at the top of the stack to a nonterminal A, given the production 归约：栈的顶部形成子串，就是接下来要归约的子串，把产生式右边的α弹出，把非终结符A压进去

因此自底向上分析也叫shift-reduce parsing

例子：
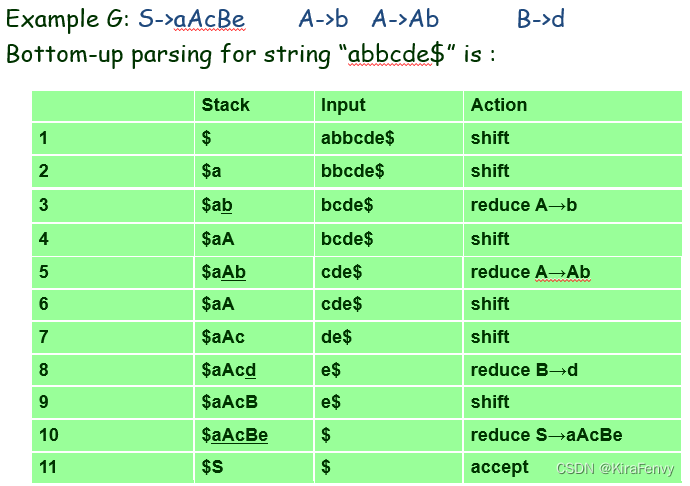
在这里插入图片描述

自下而上解析的特点

Right Sentential Form 右句型
Viable Prefix 可行前缀
Handle 句柄

右句型

A shift-reduce parser traces out a rightmost derivationof the input string in reverse order 最右推导（从右向左扫，先替换最右边的匹配的非终结符）的逆过程就是归约（因此规约是从左向右换）

最右推导及过程中得到的句型都为右句型

例子：
在这里插入图片描述
重复从字符串输入移入（shift）到堆栈，直到可以执行归约（reduce）以获得下一个正确的句子形式

每个右句型是shift-reduce parsing的一个中间结果
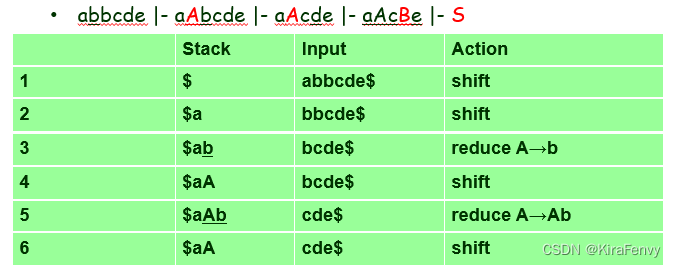
在这里插入图片描述

Viable Prefix 可行前缀

解析堆栈上的符号序列（即Stack那一列出现过的）称为右句型的可行前缀

例如
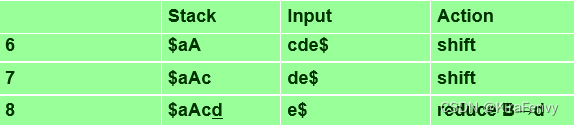
在这里插入图片描述
对应的右句型为aAcde，则其可行前缀有aA, aAc, aAcd

只要解析堆栈的内容是右子句型的可行前缀，shift-reduce parsing就是正确的

句柄

右句型γ句柄是与产生式 A->β的右侧匹配的子字符串β，可以替换为 A 以在γ的最右推导中生成以前的右句型

在这里插入图片描述

例子：根据产生式和给出的串，写出字符串的句柄
首先写出开始符号的最右推导，最后一步替换出来的子串就是句柄
在这里插入图片描述

但是，在许多情况下，与某些生产 A->β 的右侧匹配的最左侧子字符串β可能不是句柄，因为产生式 A->β 的归约会产生不是右句型的字符串。（即不是右句型，无法被归约为开始符号）

例如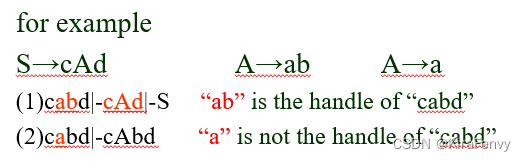：在这里插入图片描述

小结

句柄和可行前缀
- 可行前缀是右句型的前缀，从左到右不超过该句型的句柄的右端。
  - 假设右子句型是aAbcde， Ab是句柄
  - 则可行前缀为a, aA, aAb
句柄与shift-reduce parsing
- 确定解析器中的下一个句柄是 shift-reduce 解析器的主要任务
- 当下一个句柄位于堆栈顶部时，将执行“归约”操作
- 当下一个句柄尚未在堆栈顶部形成时，将执行操作“shift”
自下而上分析与可行前缀和句柄的关系
- Parser不断将可行前缀放在堆栈中
- 只要堆栈的内容是可行前缀，解析就是正确的
- 当句柄位于堆栈顶部时，进行归约

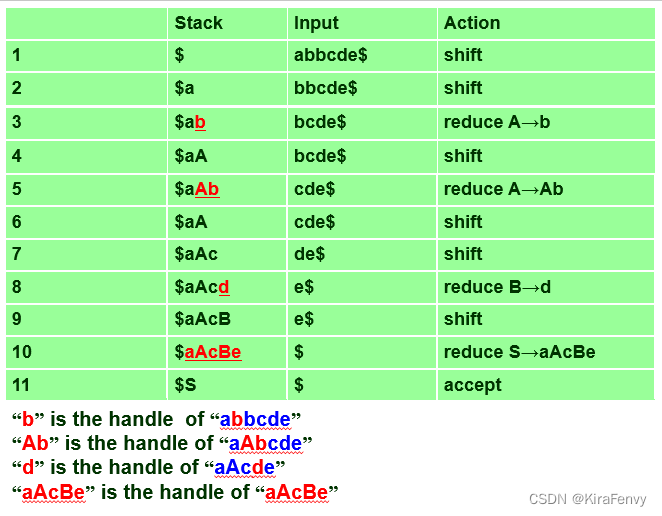
在这里插入图片描述

LR Parsing

L indicates that the input is processed from left to right L 表示输入从左到右处理
R indicates that a rightmost derivation is produced R 表示生成最右推导
K for the number of input symbols of lookahead that are used in making parsing decisions K 表示用于做出解析决策的前瞻输入符号的数

主要的三种：

LR（0）解析，在做出解析决策时不参考前瞻符号
SLR(1) parsing (simple LR(1)) is an improvement on LR(0)
- SLR（1）解析（简单 LR（1））是对 LR（0）的改进
LR(1) parsing is the most powerful and most complex (with one lookahead symbol) LR（1）解析是最强大和最复杂的（只有一个前瞻符号）

Parsing Table

每行代表一个状态，每列是一个语法符号

ACTION: take a state and a terminal symbol, determine the next action to take place 获取状态和终结符，确定要发生的下一个操作
GOTO: take a state and a grammar symbol, determine the next state 获取状态和语法符号（终结非终结都可），确定下一个状态

GOTO的Parsing Table仅保留非终结符就行
在这里插入图片描述

Shift(sk)
将符号 ai 和状态 K 放入堆栈中
Reduction(rk)
按 k个产生式（A->γ）减少，该操作包括：
从堆栈中弹出字符串γ及其所有相应的状态。假设当前堆栈的顶部是状态 Si
将 A 推到堆栈上
将状态 Sj =GOTO[Si，A] 推到堆栈上
Accept
表示解析成功完成
Error (Empty)
指示分析已发现错误

例子：
这是泛用的Parsing Table
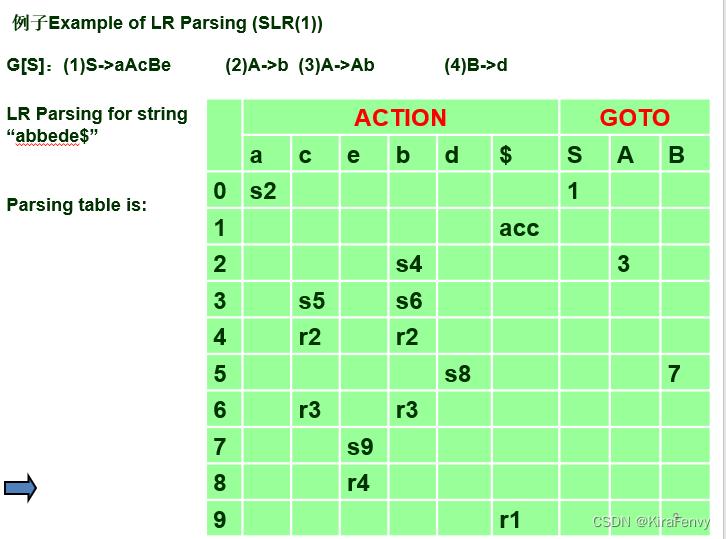
在这里插入图片描述

这是利用Parsing table的parsing过程（LR Parser）
在这里插入图片描述

Finite Automata of LR(0) Items and LR(0) Parsing LR（0）项的有穷自动机和 LR（0）分析解析

使用 LR（0）解析表的 LR 解析器是 LR（0）解析器;可以构造 LR（0）解析表的语法称为 LR（0）语法
LR（0）解析器仅使用堆栈的内容来确定句柄，它不需要输入token作为前瞻
几乎所有“真正的”语法都不是 LR（0），但 LR（0）方法是学习 LR 解析的良好起点

LR(0) items （难点）

我们需要能通过上下文无关文法（产生式）写出其LR（0）项

语法 G 的 LR（0）项是 G 的产生式，其右侧具有可区分的位置

例如，产生式 U→XYZ 有四个项
[0] U→ • XYZ [1]U→X • YZ
[2] U→XY • Z [3]U→XYZ •
产生式 A→ε只有一个项目 A→•
这些项称为 LR（0）项，因为它们不包含对前瞻的显式引用

项是记录识别产生式右侧的中间步骤

A→ • βγ 表示我们可能即将通过使用产生式A→ βγ来识别 A
A→β • γ表示已经识别了β（β必须出现在堆栈顶部）
A→ βγ • 表示 βγ 现在位于堆栈的顶部，可能是句柄，而 A-> βγ 将用于下一次归约

在这里插入图片描述

LR（0）项可以用作有限自动机的状态，该状态维护有关解析堆栈和移位-归约解析进度的信息

1 构建 LR（0）项的 NFA
2 直接构造 LR（0）项集合的 DFA（重点）
- 在构造 DFA 之前，首先通过单个产生式 S‘->S 来增广语法，其中 S’ 是一个新的非终结符，它成为增广语法的开始符号
- S’-> •S 成为 DFA 启动状态的第一个item

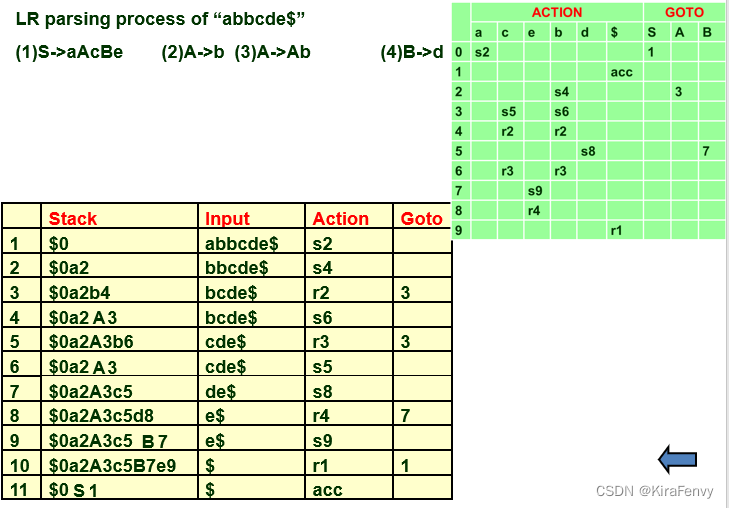
例子：在这里插入图片描述

符号 X 从状态 i 到状态 j 的转换：

如果 X 是一个标记，则此转换对应于解析期间 X 从输入到堆栈顶部的偏移
如果 X∈VN，则此转换对应于将 X 推送到堆栈上。它只能在产生式 X→r 的归约期间发生
如何构建从一种状态到另一种状态的过渡?—-goto 操作

通过LR（0）项的集合直接构造DFA（重点）

闭包操作

如果 I 是一组 LR（0）项，则closure（I）是由 I 构造的一组项，由以下规则构造：

a) 最初，closure（I） = I;
b) 如果 A->α•Bβ 在closure（I）中 并且 B ∈VN （B是非终结符） ，则对于每个产生式 B→r，将项 B→•r 添加到closure（I）
c) 重复 b）直到不再添加新项

如果**‘ • ’ 在最右端或者后面只有终结符**，闭包就是项本身

例子：
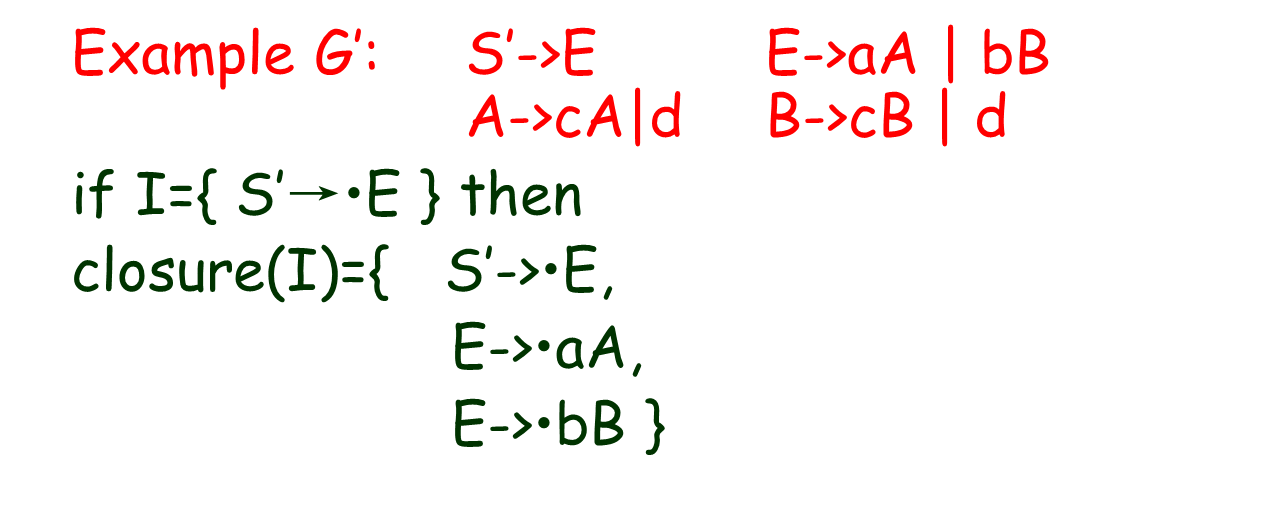
在这里插入图片描述

goto操作

X∈VN∪VT
goto(I, X)= closure(J)
其中 J 是所有项目 [ A→αX•β] 的集合，使得 [A→α• Xβ] 在 I 中

在这里插入图片描述

DFA的构造

a) closure({S’→•S}) 是 DFA 的开始状态，它是未标记的
b) 从 DFA 获取未标记的状态
I

S

i

IS_i

$I S_{i}$
- 标记 $IS_i ISi$
- 对于 $IS_i ISi 的每个项 U->x•Ry （R∈ VN∪VT，x 和 y 是字符串），计算 g o t o （ I S i ， R ） = I S j goto（IS_i，R）=IS_j goto（ISi，R）=ISj 将 I S j IS_j ISj 添加到 DFA 作为未标记（如果不存在）在 R 上添加 I S i IS_i ISi 到 I S j IS_j ISj 的转换$
c) 重复 b）直到 DFA 中没有未标记的状态

例子：
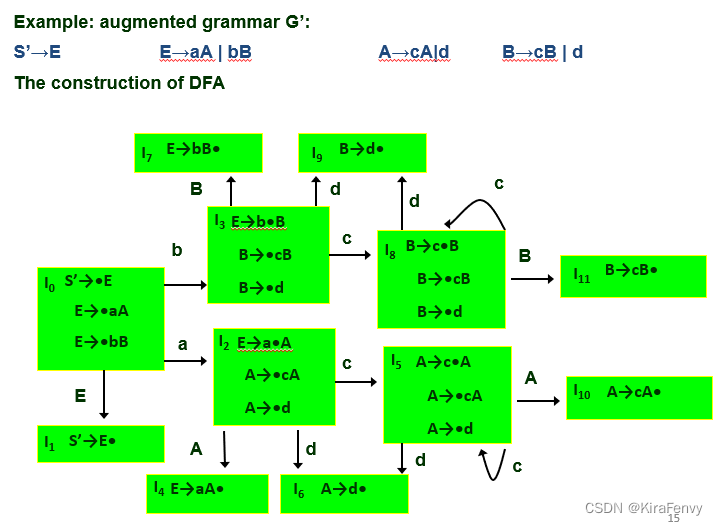
在这里插入图片描述

构造LR（0）分析表

给定一个语法 G，我们增广 G 以产生 G’
构造 G’ 的 LR（0）项集合的 DFA
状态 K 的 ACTION 部分确定如下：（将每个状态映射到一个操作）
- 如果 A→α•β∈K ，则 ACTION[K]=Shift
- 如果 A→α•∈K（归约项），并且 A→α 的标号为 j，则设置 ACTION[K]=Rj
状态 K 的 GOTO 部分（将状态/符号对映射到下一个状态）是使用以下规则为所有符号构造的：如果 goto（K，X）=J， X∈VN∪VT∪{$}，则设置 GOTO[K，X]=J

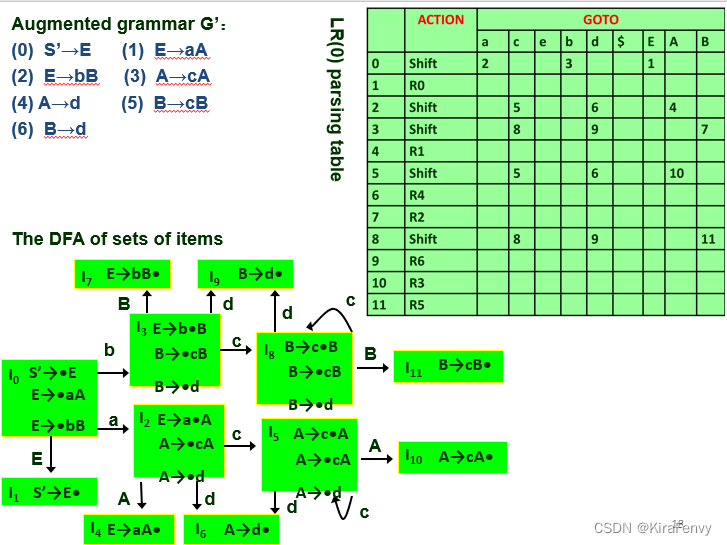
SLR（1）Parsing

项的冲突：

Shift-Reduce Conflict 移入归约冲突
- 如果集合包含移入项 A→α•aβ 和完成项complete item B→r•，则对于是shift“a”还是将“r”reduce为 B 会出现分歧
Reduce-Reduce Conflict 归约归约冲突
- 如果一个集合包含完成项complete item A→β•和B→r •，则在使用哪个产生式进行reduction方面会出现歧义。
当且仅当项目集中没有 Shift-Reduce 冲突或Reduce-Reduce冲突时才是LR（0）文法

例子：判断是否为LR（0）文法

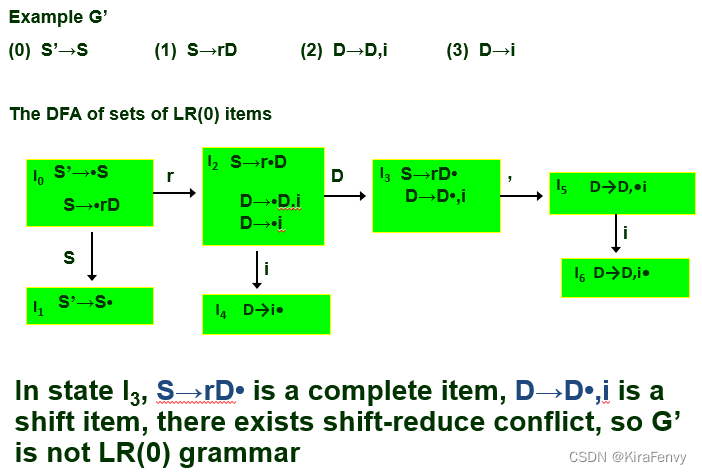
在这里插入图片描述

SLR（1）消除冲突

SLR（1）解析是 LR（0）的简单、有效的扩展
使用LR（0）项的集合构造的DFA
通过使用输入字符串中的下一个标记来指导其操作，从而提高 LR（0）解析的能力
它在转换之前查询输入token，以确保存在适当的 DFA 转换
它使用非终结符的FOLLOW集来决定是否应进行归约 For item A→r•, reduction only takes place when the next token a∈FOLLOW(A) a在A的FOLLOW集里面才能归约

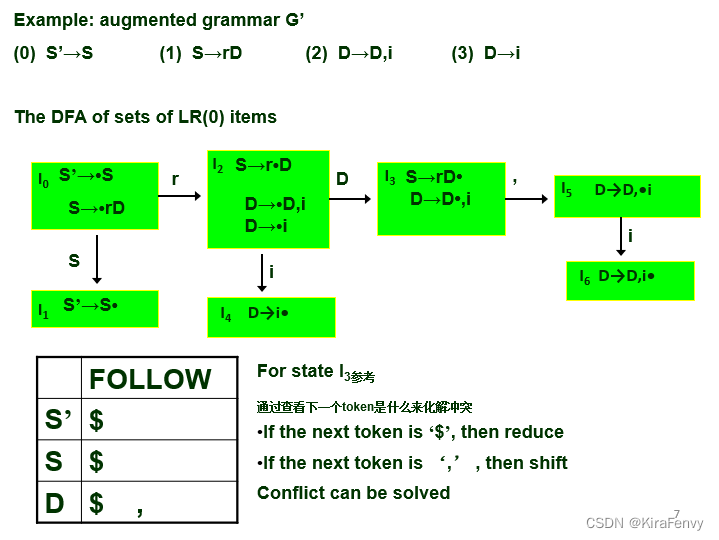
在这里插入图片描述

具体消除冲突操作规则：
I={X→α•bβ‚Α→r•‚Β→δ•}, where b∈VT，
if FOLLOW(A) ∩FOLLOW(B)=φ and not includes b, the action for I is based on the next input token ‘a’ 如果A和B的FOLLOW集无交集则 I 的操作基于下一个输入标记“a”

If a=b, then shift
If a∈FOLLOW(A), then reduce with A→r
If a∈FOLLOW(B), then reduce with B→δ
Otherwise, an error occurs

构造SLR（1）分析表

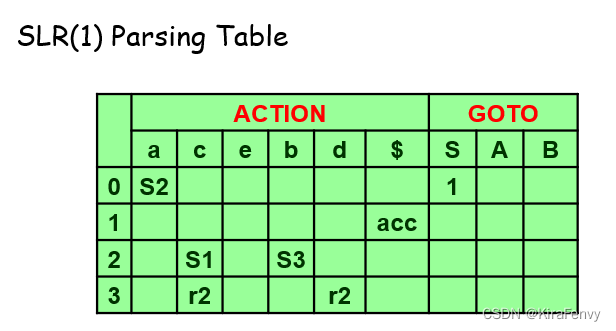
在这里插入图片描述

步骤如下：

构造 LR（0）项集合的 DFA
确定状态K的action部分
a. 如果 A→α•aβ∈K、a∈VT (句点后面是终结符)，移入， goto（K，a）=J，把 Sj填入K行a列
b. 如果 A→α•∈K （句点后面没东西），并且对应的产生式 A→α 的标号为 j，则为每个 b∈Follow（A）设置 ACTION[K，b]=Rj
c. 如果 S’→S•∈K，则设置 ACTION[K，$]=‘acc’
状态 K 的 GOTO 部分是使用以下规则为所有非终结符构造的：如果 A→α•Bβ∈K、B∈VN 和 goto（K，B）=J，则设置 GOTO[K，B]=‘J’

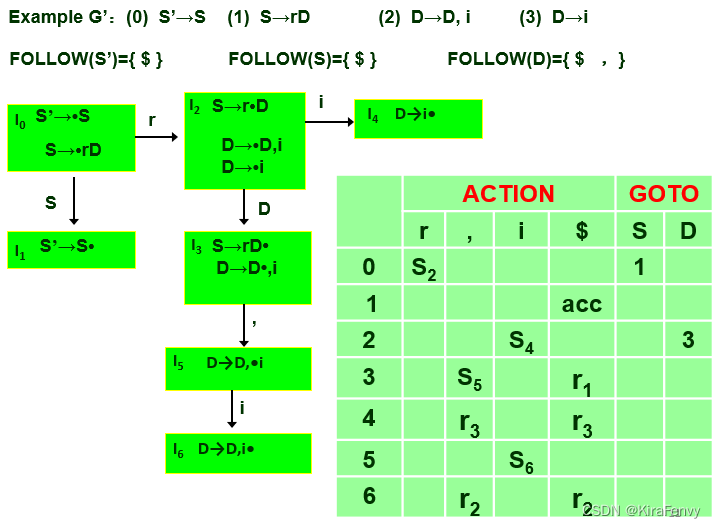
例子：
在这里插入图片描述

语义分析 Semantic Analysis

语义分析概述

语义：与正在翻译的程序的最终含义密切相关的信息
语义分析：分析编程语言语义规则所需的程序，以确定其正确性并保证正确执行

类型检查：
运算符的操作数类型是否相等？
赋值assignment的左侧和右侧的类型是否相等？
形参的类型是否与对应的实参相同？
数组的索引类型是否合适？

是否已声明使用的标识符？
V 是否已声明为“V[E]”的数组类型的变量？

构建符号表以跟踪声明中建立的名称的含义
对表达式和语句执行类型检查，以确定它们在语言类型规则中的正确性

属性与属性文法

属性的定义：属性是编程语言构造的任何属性
属性包括：
变量的数据类型 The data type of a variable
表达式的值 The value of an expression
过程的目标代码 The object code of a procedure

属性语法用来描述语义规则

属性直接与语法符号（终结符和非终结符）相关联

如果 X 是语法符号，a 是与 X 关联的属性，则与 X 关联的 a 的值写为 X.a

属性 a1,…,ak 的属性语法是语言的所有语法规则的所有属性方程的集合
通常，属性语法以表格形式编写
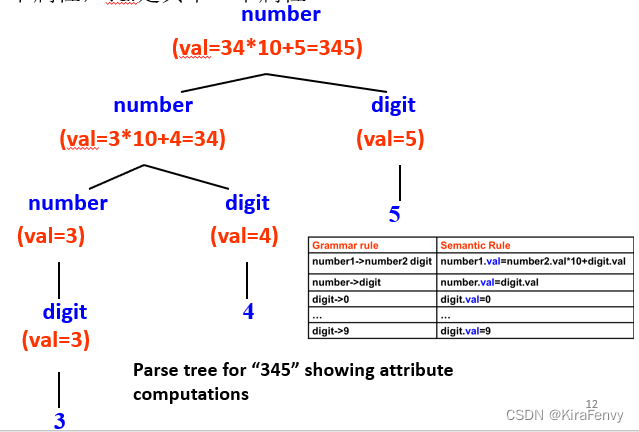
在这里插入图片描述
例1：无符号数对应的属性语法
无符号数的属性就是值

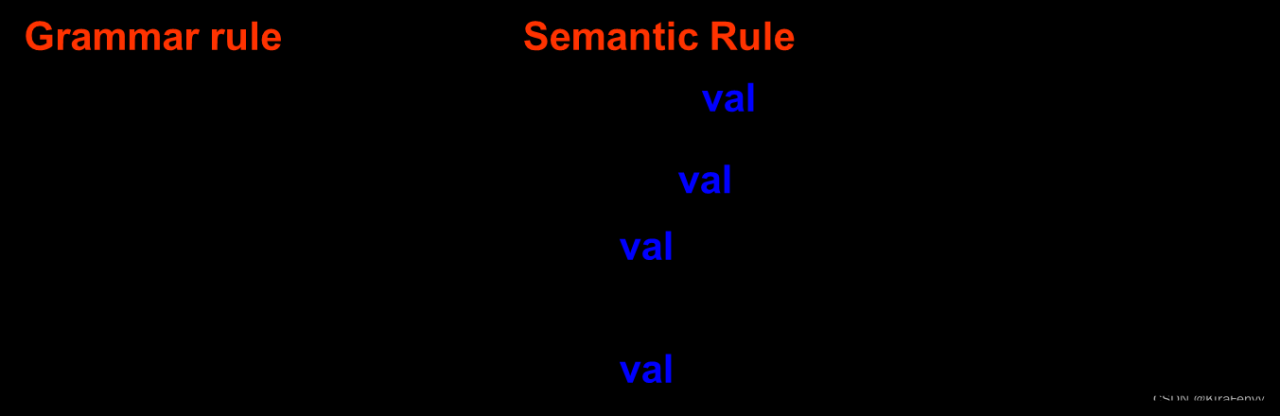
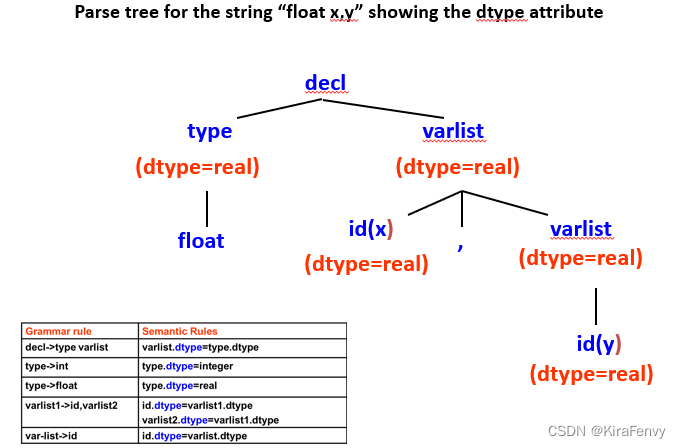
在这里插入图片描述

例2：变量声明对应的属性语法.
变量声明的属性就是数据类型
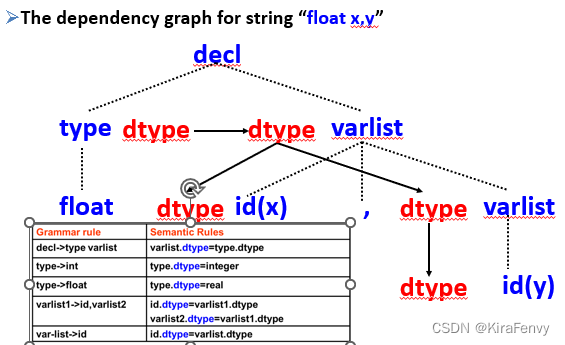
在这里插入图片描述

依赖图和属性计算 Dependency Graphs and Algorithms for Attribute Computation（掌握）

依赖图 Dependency Graphs

给定属性语法，每个语法规则都有一个关联的依赖关系图
每个符号的每个属性 Xi.aj 对应一个节点
对于每个属性方程 Xi.aj=fij（…，Xm.ak,…），从右侧的每个节点 Xm.ak 到节点 Xi.aj 都有一个边（表示 Xi.aj 对 Xm.ak 的依赖性）

三个属性语法的依赖关系图：
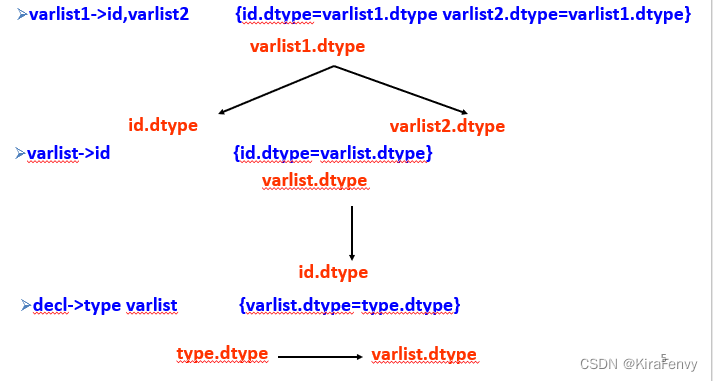
在这里插入图片描述

由上下文无关语法生成的合法字符串的依赖关系图是表示字符串解析树的每个节点的语法规则选择的依赖关系图的联合（很拗口，也就是说多个规则组成一个大规则）
在这里插入图片描述

Synthesized and Inherited Attributes 综合属性和继承属性

属性评估依赖于解析树的显式或隐式遍历
不同类型的遍历在可以处理的属性依赖关系类型方面的能力各不相同
根据属性表现出的依赖类型对属性进行分类，可以分为
- Synthesized attribute 综合属性
- Inherited attribute 继承属性

综合属性 Synthesized Attribute

依赖关系从下面指向上面（儿子节点指向父亲节点）
等号左边出现小a，右边每个产生式都要有k个小a
A.a=f（x1.a1,…X1.ak,…,Xn.a1,…Xn.ak）

如图，val属性是Synthesized Attribute
在这里插入图片描述

假设解析树或语法树已由解析器构造
合成的属性值可以通过树的单个自下而上或后序遍历来计算
先计算儿子节点的综合属性，再往上算

继承属性 Inherited Attribute

继承的属性具有从解析树中的父级流向子级或从同级流向同级的依赖项
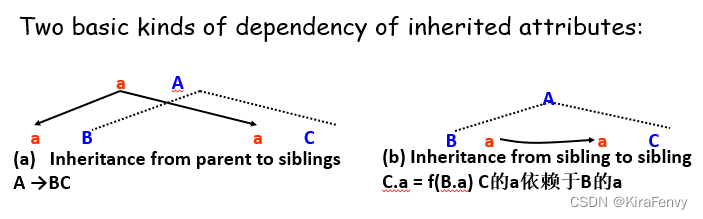
在这里插入图片描述
在变量声明的属性文法中，dtype是继承属性

继承的属性可以通过解析树或语法树的先序遍历来计算，计算T的每个儿子的继承属性，从上往下递归算

与综合属性不同，由于继承的属性可能在儿子节点属性之间具有依赖关系，因此计算子项的继承属性的顺序非常重要

中间代码生成 Intermediate code generation

代码生成的任务是为目标计算机生成可执行代码，该代码表示源代码的语义

代码生成通常分为几个步骤
1.Intermediate code generation（与机器无关）
2.生成某种形式的汇编代码
3.优化：提高目标代码的速度和大小

三地址码 Three-Address Code

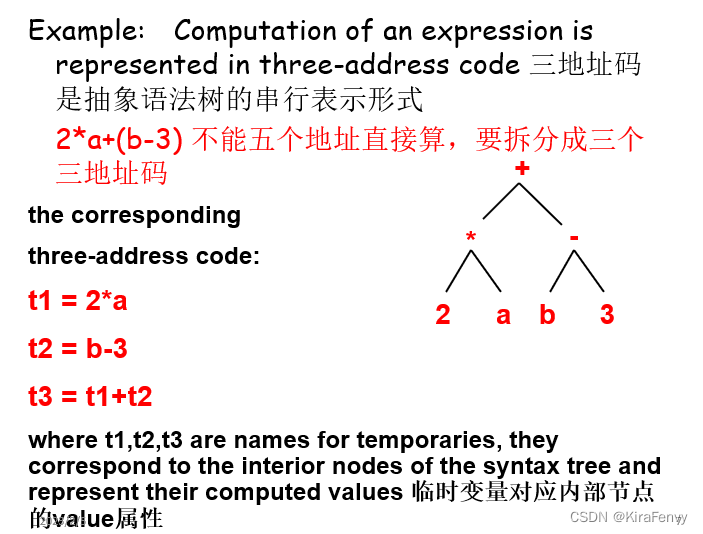
中间代码有很多种，前面说到的抽象语法树也是一种，但是与实际代码相去甚远，所以这里采用三地址码

三地址码的一般形式，y和z进行op运行赋值给x即x=y op z
其中，x，y，z 是名称、常量或编译器生成的临时名称，x、y和z各代表内存中的一个地址；op代表任何算术或逻辑运算符，例如 + 、‘and’

例如2*a+(b-3)的三地址码：
在这里插入图片描述

三地址码只要不超过3个地址就行，下面是9种形式：

赋值语句的形式为 “x=y op z”，其中 op 是二进制操作
赋值语句的形式为 “x=op y”，其中 op 是一元运算
拷贝语句的形式为 “x=y”，其中 y 的值赋值为 x
“goto L” 无条件跳转指令，L代表某一条指令的地址
“if B goto L” , “if_false B goto L”有条件就跳转，不满足条件B（Boolean）就不跳转
“Label L” 标号定义语句，定义后面那句语句的地址
“read x”
“write x”
“halt” 表示三地址码的结束

下面是将源代码改写为三地址码的例子：
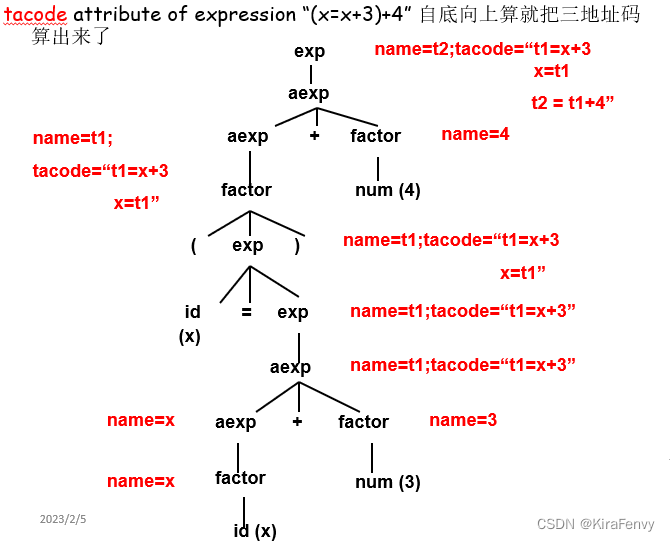
在这里插入图片描述

代码生成技术

生成的三地址代码被视为字符串属性
中间代码成为可以使用属性语法定义并由语法树的后序遍历生成的synthesized attribute合成属性

三地址码的属性语法：

tacode for three-address code 表示程序语句或表达式的三地址码属性（字符串类型属性）
name 为表达式中的中间结果生成的临时名称的名称

字符串串联的符号：

++ 用于与有换行符的字符串连接
|| 用于与有空格的字符串连接

函数：
newtemp（）：返回一个新的临时名称

例子：
给定表达式的语法：
exp -> id=exp | aexp
aexp -> aexp+factor | factor
factor -> (exp) | num | id
假定令牌 id标识符和 num整型常量具有预先计算的属性 strval，该属性是token的字符串值

对应的属性语法
在这里插入图片描述
再改写成三地址码，由于三地址码属性是综合属性，因此自底向上计算

控制语句和逻辑表达式的代码生成

前面主要是用于赋值和简单算术表达式的代码生成
现在说说控制语句和逻辑表达式的代码生成
在这里插入图片描述

逻辑表达式（或布尔表达式）由应用于布尔变量或关系表达式元素的布尔运算符（and，or，not）组成
- 关系表达式的形式为 “E1 relop E2”，其中 E1 和 E2 是算术表达式，relop 是一个比较运算符
由以下语法生成的布尔表达式 E->E or E | E and E | not E | (E)
| id relop id | true | false
- or 和 and 是左关联，or具有最低优先级，not右关联最高优先级

如果布尔表达式用于计算逻辑值，则布尔表达式将以类似于算术表达式的方式进行转换

例子：
在这里插入图片描述
如果将它们用作控制语句上下文中的测试，例如 if-then 或 while-do，则布尔表达式的值不会临时保存，而是由程序中达到的位置表示

控制语句代码生成

下面是控制语句的语法：
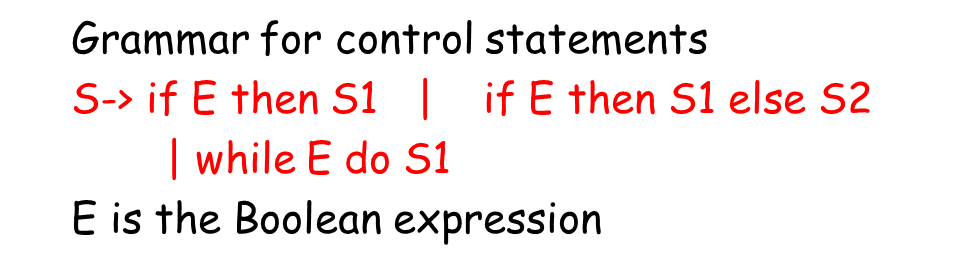
在这里插入图片描述

控制语句上下文中布尔表达式的翻译：

E.true (E.false) 表示布尔表达式的真假出口
S.next 是S 代码之后要执行的第一个三地址指令的标签
S.begin 表示整个S的第一条指令
newlabel（）每次调用时都会返回一个新标签

在这里插入图片描述
类型1：S->if E then S1

E.true 是附加到 S1 代码生成的第一条指令
E.false 是附加到 S 代码之后要执行的第一个指令
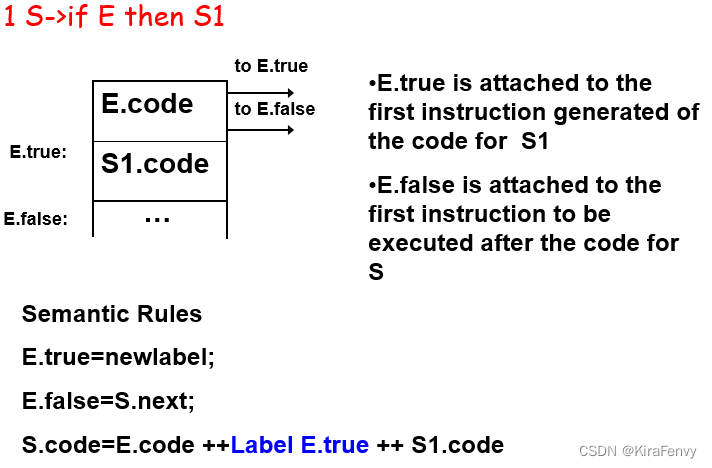
在这里插入图片描述
类型2：S->if E then S1 else S2
E.true 附加到 S1 代码的第一条指令
E.false 附加到 S2 代码的第一条指令

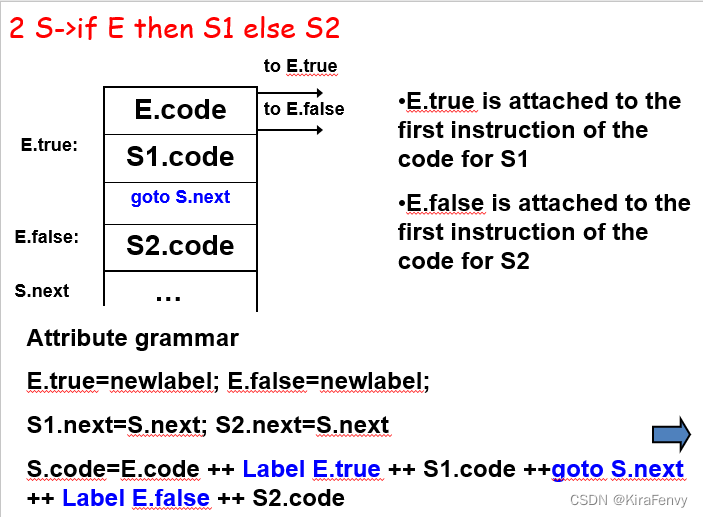
在这里插入图片描述
类型3：S->while E do S1

E.true 附加到 S1 代码的第一条指令
E.false 附加到 S 代码之后要执行的第一个指令

在这里插入图片描述

包含逻辑表达式的代码生成

基本形式：
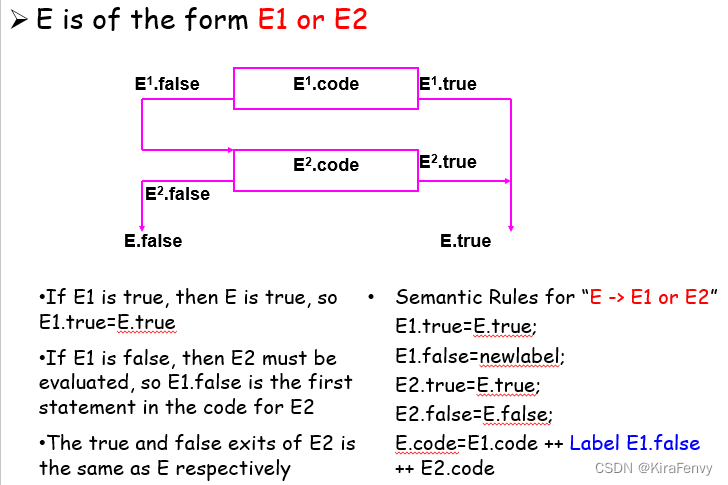
在这里插入图片描述
例1：E -> E1 or E2
先判断E1，E1.true则E.true
若E1.false，则创建新标签，判断E2，E2的真假出口和E相同

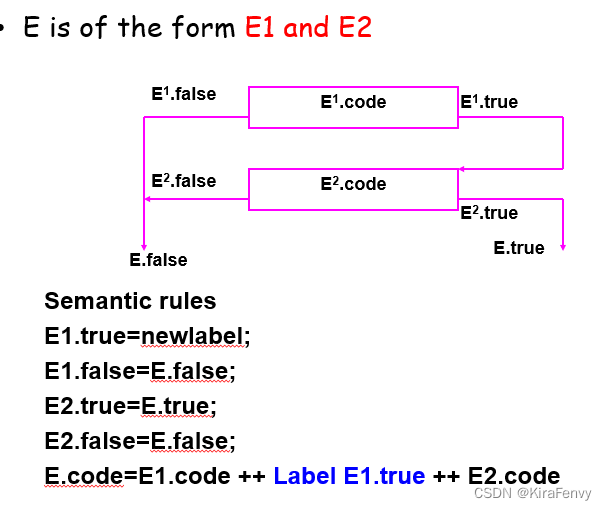
例2：E -> E1 and E2

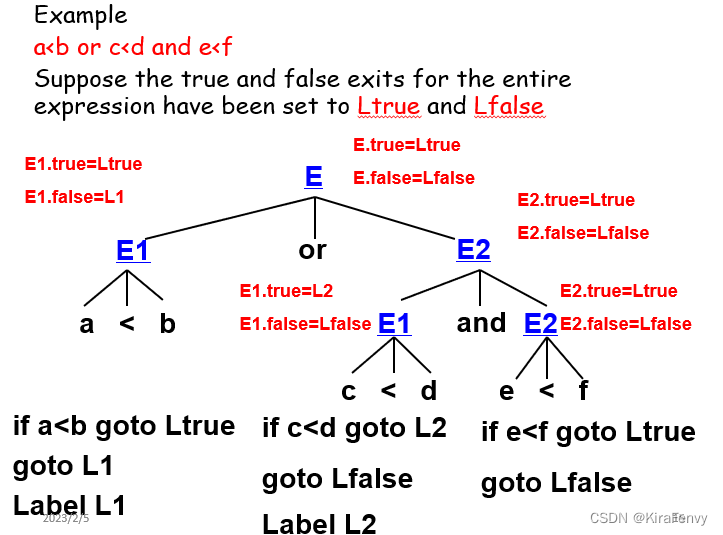
在这里插入图片描述

例3：关系运算a<b or c<d and e<f
假设整个表达式的 true 和 false 出口已设置为 Ltrue 和 Lfalse

在这里插入图片描述

例4：
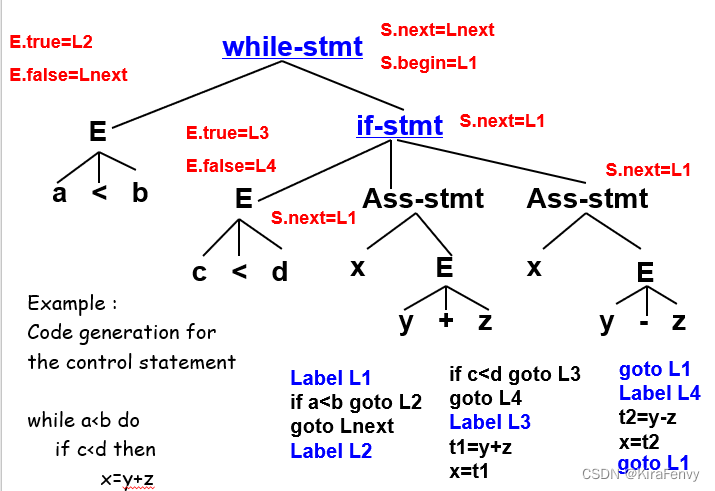
下述控制语句的代码生成在这里插入图片描述

原文链接：https://blog.csdn.net/m0_51371693/article/details/128858842

这里写自定义目录标题

编译器

概念

Interpreter and Compiler 解释器和编译器

编译器工作流程

词法分析 Lexical Analysis

字母表，字符串和语言

正则表达式 Regular Expressions

Atomic Regular Expressions 原子正则表达式

Compound Regular Expressions 复合正则表达式

Finite Automata 有限自动机

有限自动机图示

NFA和DFA

正则表达式转换为NFA

NFA转化为DFA

Minimizing DFA 最小化DFA

Confliction Resolutions 冲突解决

Syntax Analysis 语法分析

Context-Free Grammars 上下文无关文法

定义

推导Derivation

传递闭包

Sentence句子

Parse Trees语法分析树

最左推导 LeftMost Derivation

最右推导

抽象语法树 Abstract Syntax Trees（AST）

二义性ambiguity

自顶向下分析 Top-Down Parsing

First集

Follow集

LL（1）文法

LL（1）文法定义

判定LL（1）文法方法(重点）

可空非终结符集合的计算

计算First集

计算每个非终结符的Follow集

通过LL(1)文法定义来识别LL（1）文法

将非LL（1）文法转化为LL（1）文法

左公因子

左递归

消除左递归 Left Recursion Removal

消除左公因子 Left Factoring

递归下降分析 Recursive-Descent Parsing

构造递归下降分析的过程

1. 消除G的左递归或左公因式成为G’

2. 判断G’是否符合LL（1）文法

3. 构造G’的递归下降分析

LL（1）分析 LL(1) parsing

LL（1）分析流程

LL（1）分析表

构造LL（1）分析表

自底向上分析

自底向上分析概述

主要思想

自底向上分析的实现

自下而上解析的特点

右句型

Viable Prefix 可行前缀

句柄

小结

LR Parsing

Parsing Table

Finite Automata of LR(0) Items and LR(0) Parsing LR（0） 项的有穷自动机和 LR（0） 分析解析

LR(0) items （难点）

通过LR（0）项的集合直接构造DFA（重点）

闭包操作

goto操作

DFA的构造

构造LR（0）分析表

SLR（1）Parsing

SLR（1）消除冲突

构造SLR（1）分析表

语义分析 Semantic Analysis

语义分析概述

属性与属性文法

依赖图和属性计算 Dependency Graphs and Algorithms for Attribute Computation（掌握）

依赖图 Dependency Graphs

Synthesized and Inherited Attributes 综合属性和继承属性

综合属性 Synthesized Attribute

Finite Automata of LR(0) Items and LR(0) Parsing LR（0）项的有穷自动机和 LR（0）分析解析