神经网络的传递过程
https://zhuanlan.zhihu.com/p/65472471
https://blog.csdn.net/weixin_39445556/article/details/81416133
https://blog.csdn.net/weixin_39445556/article/details/83543945
https://blog.csdn.net/weixin_39445556/article/details/83661219
https://blog.csdn.net/weixin_39445556/article/details/83930186
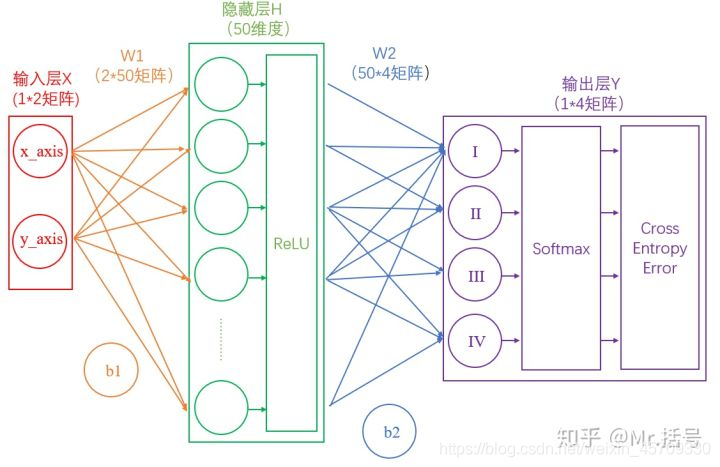
引用了一下知乎上一位大佬的图
这是一个简单的神经网络,有两层网络组成
正向传播
就是我们的数据从神经网络的输入层通过神经网络传输到输出层的过程。下面将按照顺序进行解释
核心思路:传递的过程其实就是矩阵的乘法以及计算加权平均后经过激活函数就完成了一次传递,以此类推进行传递
1.数据输入网络
输入层:输入层中输入的是一些矩阵,比如可以输入
(
1
,
2
)
(1,2)
(1,2)这个点坐标作为一个数据,也可以输入一张256*256的图像作为数据。
2.传递到隐藏层
通过矩阵的乘法,输入的
X
X
X乘上一个权重矩阵
W
W
W。公式表示为
h
(
X
)
=
W
T
⋅
X
+
b
h(X)=W^T\cdot X+b
h(X)=WT⋅X+b
其中
b
b
b为偏置。
展开来写就是
h
(
x
1
,
x
2
,
⋯
,
x
n
)
=
w
1
x
1
+
w
2
x
2
+
⋯
+
w
n
x
n
+
b
h(x_1,x_2,\dotsm,x_n)=w_1x_1+w2x2+\dotsm+w_nx_n+b
h(x1,x2,⋯,xn)=w1x1+w2x2+⋯+wnxn+b
这也就是求一个加权平均,也是一个多元线性回归。
如果有多层神经网络,那么
h
h
h相当于就是第一次把数据输入隐藏层中的
X
X
X,继续代入公式就变成了
h
(
h
(
X
)
)
h(h(X))
h(h(X))。
有多少层神经网络就进行多少次迭代。
3.神经元激活
每一次完成一次传递之后,就要通过一个激活函数对其进行激活。不然刚才的线性运算就是没有意义的,只是单纯的计算。
可以理解为经过计算之后,要用激活函数把神经元给激活了,这个神经元才有用,跟人脑一样。
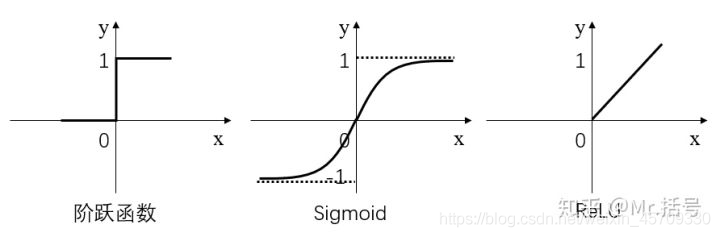
主要就是有三种激活函数
S
i
g
n
、
S
i
g
m
o
i
d
、
R
e
L
U
Sign、Sigmoid、ReLU
Sign、Sigmoid、ReLU
表达式分别为
S
i
g
n
(
x
)
=
{
1
x
≥
0
0
x
≤
0
Sign(x)=\begin{cases} 1 & x\geq 0\\ 0 & x\leq 0 \end{cases}
Sign(x)={10x≥0x≤0
S
i
g
m
o
i
d
(
x
)
=
tanh
(
x
)
Sigmoid(x)=\tanh(x)
Sigmoid(x)=tanh(x)
R
e
L
U
(
x
)
=
{
x
x
≥
0
0
x
≤
0
ReLU(x)=\begin{cases} x & x\geq 0\\ 0 & x\leq 0 \end{cases}
ReLU(x)={x0x≥0x≤0
4.从隐藏层输出
经过若干个隐藏层之后,到最后进行输出时,也是乘另一个权重矩阵
W
o
u
t
p
u
t
W_{output}
Woutput。公式表示为:
O
u
t
p
u
t
(
X
)
=
W
o
u
t
p
u
t
⋅
H
+
b
0
Output(X)=W_{output}\cdot H+b_0
Output(X)=Woutput⋅H+b0
其中
H
H
H表示经过多神经网络的多次传递之后得到最终的数据。
5.输出正规化
因为从神经网络出来的数值不一定是一个
0
−
1
0-1
0−1的数,可能是比1大的,所以我们需要进行规范数据,变成我们之后能用到的概率。
通常就是使用
s
o
f
t
m
a
x
softmax
softmax函数
s
o
f
t
m
a
x
(
x
)
=
e
i
∑
j
e
j
softmax(x)=\frac{e^i}{\sum_je^j}
softmax(x)=∑jejei
计算的过程是:
(1)以
e
e
e为底对所有元素求指数幂;
(2)将所有指数幂求和;
(3)分别将这些指数幂与该和做商。
这样求出的结果中,所有元素的和一定为1,而每个元素可以代表概率值。
6.开始进行损失计算
通过损失函数,进行对结果进行损失的计算
- 均方误差函数(MSE)(类似于方差的计算)
M
S
E
=
1
N
∑
i
=
1
N
(
y
t
r
u
e
i
−
y
p
r
e
d
i
)
2
MSE=\frac{1}{N}\sum^{N}_{i=1}(y_{true_i}-y_{pred_i})^2
MSE=N1i=1∑N(ytruei−ypredi)2
可以理解为反映了预测点在实际曲线周围的偏离程度。
- 均方根误差函数(RMSE)(类似于标准差的计算)
R
M
S
E
=
1
N
∑
i
=
1
N
(
y
t
r
u
e
i
−
y
p
r
e
d
i
)
2
RMSE=\sqrt{\frac{1}{N}\sum^{N}_{i=1}(y_{true_i}-y_{pred_i})^2}
RMSE=N1i=1∑N(ytruei−ypredi)2
可以理解为反映了预测点在实际曲线周围的偏离程度的开方
- 平均绝对误差函数(MAE)(类似于两点间的距离)
M
A
E
=
1
N
∑
i
=
1
N
∣
(
y
t
r
u
e
i
−
y
p
r
e
d
i
)
∣
MAE=\frac{1}{N}\sum^{N}_{i=1}|(y_{true_i}-y_{pred_i})|
MAE=N1i=1∑N∣(ytruei−ypredi)∣
可以理解为反映了预测值与真实值的距离
以上均是值越小越好。
还有交叉熵损失等
损失越小,说明网络的效果越好
7.进行后向传播
后向传播就是一个参数优化的过程,也就是优化
W
W
W和
b
b
b,计算完损失之后进行后向传播,根据得到的损失值进行后向传播。而为了进行优化,就是通过梯度下降的方法对
W
W
W和
b
b
b进行参数调整。
8.迭代
通过不断多次迭代,不断地对网络参数进行优化调整,直到损失降低到比较低,且逐步收敛模型就训练完毕,之后还要通过对于测试的结果再进行部分微调。