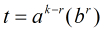博客

题目：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=5237

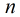
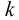
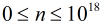
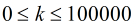
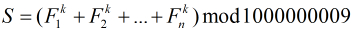
题意：给定和，其中，，求  的值。

分析：嗯，这道题貌似有难度，如果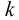比较小的话我们可以构造矩阵，实际上这样做也挺麻烦的。

     以前我们做一个大Fibonacci数列模一个大素数都是用矩阵，当然这里素数满足条件：5是模这个素数的二

     次剩余，那么现在要求不要用矩阵来计算这个结果呢？那就是今天我要讨论的问题，本题也是基于这种思路。

     本题我们可以直接利用Fibonacci数列的公式进行计算。因为我们知道Fibonacci数列的公式为：

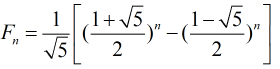
     虽然公式中含有根号，但是我们知道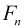是一个整数，而且5是模1000000009的二次剩余。那么可以通过逆元

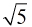
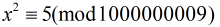
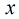
     和二次剩余的转化来做。比如就可以用中的来代替。

     为了方便表示，我们令：

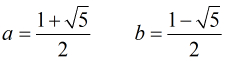
     那么得到

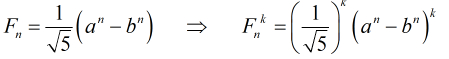
     把按照二项式展开得到

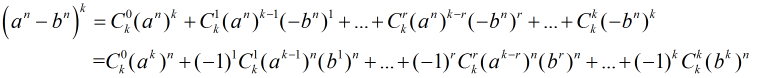
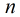
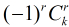
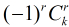
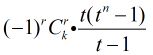     对于每一个都这样表示，那么相同的合并后是等比数列，比如对于所有系数为合并后为

     ， 其中

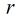
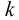
     所以到了这里本题就明确了，枚举每一个从0到，依次计算即可。

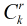
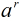
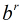
     当然对于，我们可以阶乘预处理然后求逆元，至于和同样预处理，这样时间少很多。

     可以看出本题条件好在1000000009是素数，而且5是模1000000009的二次剩余。

     经计算2模1000000009的逆元是500000005，而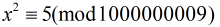的一个解为383008016。

     也就是说对于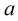有

     同理，对于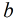有

     嗯，貌似还有一个问题没有处理，t = 1时咋办？ 这个很简单啦，不用等比求和公式即可。其实吧，这里面

     我们还可以注意到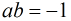，也可以进一步优化，读者自己体会，就说到这里。

代码：

#include <iostream>
#include <string.h>
#include <stdio.h>

using namespace std;
typedef long long LL;
const int N = 100005;
const LL MOD = 1000000009;

LL fac[N],A[N],B[N];

void Init()
{
    fac[0] = 1;
    for(int i=1; i<N; i++)
        fac[i] = fac[i-1] * i % MOD;
    A[0] = B[0] = 1;
    for(int i=1; i<N; i++)
    {
        A[i] = A[i-1] * 691504013 % MOD;
        B[i] = B[i-1] * 308495997 % MOD;
    }
}

LL quick_mod(LL a,LL b,LL MOD)
{
    LL ans = 1;
    a %= MOD;
    while(b)
    {
        if(b & 1)
        {
            ans = ans * a % MOD;
            b--;
        }
        b >>= 1;
        a = a * a % MOD;
    }
    return ans;
}

LL Solve(LL n,LL k)
{
    LL ans = 0;
    for(int r=0; r<=k; r++)
    {
        LL t = A[k-r] * B[r] % MOD;
        LL x = fac[k];
        LL y = fac[k-r] * fac[r] % MOD;
        LL c = x * quick_mod(y,MOD-2,MOD) % MOD;
        LL tmp = t * (quick_mod(t,n,MOD) - 1) % MOD * quick_mod(t-1,MOD-2,MOD) % MOD;
        if(t == 1) tmp = n % MOD;
        tmp = tmp * c % MOD;
        if(r & 1) ans -= tmp;
        else      ans += tmp;
        ans %= MOD;
    }
    LL m = quick_mod(383008016,MOD-2,MOD);
    ans = ans * quick_mod(m,k,MOD) % MOD;
    ans = (ans % MOD + MOD) % MOD;
    return ans;
}

int main()
{
    int T;
    LL n,k;
    Init();
    scanf("%d",&T);
    while(T--)
    {
        cin>>n>>k;
        cout<<Solve(n,k)<<endl;
    }
    return 0;
}