84. 柱状图中最大的矩形

题目链接

解题思路： 这里提供两种解题思路，即直接解题，和单调栈解题。

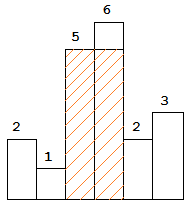
1. 直接解题，观察下图，6能覆盖5出现的情况，而5不能覆盖6的情况，因此我们会想到，在序列递增的时候可以延迟找最大矩形，而当序列开始递减时，即出现拐点，从拐点处搜索到序列起点，计算并记录这个过程出现的最大矩形，矩形的高度是向左遍历过程中的最小值。
   

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int res = 0;
        heights.push_back(0);
        int n = heights.size();
        for (int i = 0; i < n - 1; ++i) {
            if (heights[i] > heights[i + 1]) {
                int minH = heights[i];
                for (int j = i; j >= 0; --j) {
                    minH = min(minH, heights[j]);
                    res = max(res, minH * (i - j + 1));
                }
            }
        }
        return res;
    }
};

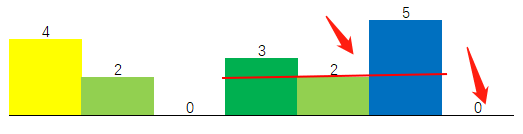
2. 单调栈解法，参考grandyang博客解法，分析解法1会发现，我们在遍历的过程中维护了一个递增序列，当出现递减元素时，开始计算（找寻）最大矩形，那么联想到单调栈解法，选取构造单调递增栈可解此题。具体的是，当栈为空或栈顶元素高度小于当前元素高度，则入栈，否则说明出现拐点，依次出栈计算以栈顶元素高度能构成的最大矩形。设计代码中有两点要注意：当出栈后，(1)栈为空时则说明出栈的元素的高度是当前访问序列中最小高度，这意味着矩形的左边界直达序列的起点，(2)当栈不为空时，我们要找寻这个出栈元素的高度对应的矩形最左边能到什么位置？最左边是当前栈顶元素对应的位置+1，而不是idx位置，举个例子，输入序列为[4,2,0,3,2,5]，组成的图形如下图，观察箭头所指区域，0触发找寻矩形，当我们出栈2元素时，高度为2的矩形左边界并不是只能到2，而是可以到左边的0，而我们分析一下这个0代表什么？0此时正处于栈顶，表示着我们在找2对应的矩形最左边界时，本质上是要找往左边看比它小的第一个元素(而这中间如果出现比2大的元素，比如3，对应的矩形面积都能收纳到2中)，那这个元素是不是恰好是栈顶元素0，其实并没有什么巧合，因为本身我们在遍历的过程中维护的单调栈就是存放递增序列的。OK，所有的细节都对上号了~，请看代码。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int res = 0;
        heights.push_back(0);
        int n = heights.size();
        stack<int> st;
        for (int i = 0; i < n; ++i) {
            if (st.empty() || heights[st.top()] < heights[i]) st.push(i);
            else {
                while (!st.empty() && heights[st.top()] > heights[i]) {
                    int idx = st.top(); st.pop();
                    int tmp;
                    if (st.empty()) tmp = heights[idx] * i;
                    else tmp = heights[idx] * (i - st.top() - 1);
                    res = max(res, tmp);
                }
                st.push(i);
            } 
        }
        return res;
    }
};

85. 最大矩形

题目链接

解题思路： 在理解了题84后解此题就非常容易了，即将此题转换到题84的场景中，先分析示例，当我们将每一层作为直方图的底，向上构造直方图，然后利用题84中的方法求这个直方图能构成的最大矩形。构造直方图的方法是，遍历原数组每层元素时，若该元素为”1″则直方图在该位置柱子的高度为上一层的+1，若该元素为0，则直方图柱子高度为0.详细内容阅读grandyang博客.

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int rows = matrix.size(), cols = matrix[0].size();
        vector<int> heights(cols, 0);
        int res = 0;
        for (int i = 0; i < rows; ++i) {
            for (int j = 0; j < cols; ++j) {
                if (matrix[i][j] == '0') heights[j] = 0;
                else heights[j] += 1;
            }
            res = max(res, helper(heights));
        }
        return res;
    }
    int helper(vector<int> heights) {
        int res = 0;
        heights.push_back(0);
        int n = heights.size();
        for (int i = 0; i < n - 1; ++i) {
            if (heights[i] > heights[i + 1]) {
                int minH = heights[i];
                for (int j = i; j >= 0; --j) {
                    minH = min(minH, heights[j]);
                    res = max(res, minH * (i - j + 1));
                }
            }
        }
        return res;
    }
};

另外，在grandyang博客中也给出了另一种解法，方法也挺新颖，这里记录一下。我们在解本题时，有时脑子里也会冒出这种想法，当我们以某个点为中心时，向两边延展，如果能找到延展的左边界和右边界，那么两边界的间距作为矩形的宽，即可用当前点所在的高度构造矩形。那么解题的关键是如何找出矩形的宽(i.e.,找出左边界和右边界)，矩形的高度依然采用解法1中的方法。某点为中心向两边能延展要符合的条件是，两边的高度不能低于当前点高度(否则不能构成矩形)，OK，解法是不是有点像
题84中解法1的方法，用高度作为判断，若探索左边界，在从当前点i向左探索，当高度比当前高度低时break，右边界同理。

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int rows = matrix.size(), cols = matrix[0].size();
        vector<int> heights(cols, 0);
        int res = 0;
        for (int i = 0; i < rows; ++i) {
            for (int j = 0; j < cols; ++j) {
                if (matrix[i][j] == '0') heights[j] = 0;
                else heights[j] += 1;
            }
            res = max(res, helper(heights, i, matrix));
        }
        return res;
    }
    int helper(vector<int> heights, int row, vector<vector<char>>& matrix) {
        int cols = matrix[0].size();
        vector<int> left(cols), right(cols);
        for (int i = 0; i < cols; ++i) {
            for (int j = i; j >= 0; --j) {
                if (heights[j] >= heights[i]) {
                    left[i] = j;
                } else break;
            }
        }
        for (int i = cols - 1; i >= 0; --i) {
            for (int j = i; j < cols; ++j) {
                if (heights[j] >= heights[i]) {
                    right[i] = j;
                } else break;
            }
        }
        int res = 0;
        for (int i = 0; i < cols; ++i) {
            res = max(res, heights[i] * (right[i] - left[i] + 1));
        }
        return res;
    }
};

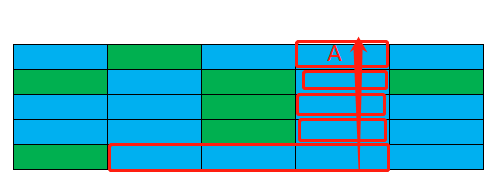
另外grandyang给出了第三种解法，从另一个角度解题，解法2是横向扩展，在题84heights的基础上解题，而解法三采取的纵向扩展，先求出每个元素水平向左连续的”1″个数，即Ones[i][j]，然后再访问一次每个元素，然后对访问元素向上扩展，结合下图解释，蓝色为1，绿色为0，假设我们当访问的位置是箭头起点，然后顺着箭头方向向上扩展，向上扩展的过程中，要取ones[x][j]路径上的最小值作为矩形宽度，对于A所在位置，应该取1，而不是去min(2,3)，即去路径访问当前最小值。

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int rows = matrix.size(), cols = matrix[0].size();
        vector<vector<int>> Ones(rows, vector<int>(cols, 0));
        int res = 0;
        for (int i = 0; i < rows; ++i) {
            for (int j = 0; j < cols; ++j) {
                if (matrix[i][j] == '1') Ones[i][j] = 1 + (j == 0 ? 0 : Ones[i][j - 1]);
            }
        }
        for (int i = 0; i < rows; ++i) {
            for (int j = 0; j < cols; ++j) {
                if (matrix[i][j] == '0') continue;
                res = max(res, Ones[i][j]);
                int mn = Ones[i][j];
                for (int k = i - 1; k >= 0 && matrix[k][j] != '0'; --k) {
                    mn = min(mn, Ones[k][j]);
                    res = max(res, mn * (i - k + 1));
                }
            }
        }
        return res;
    }
};

————————————

写在后面

1. 这两题属于矩形中求面积的题，用暴力解法很好解但是时间复杂度很高，OJ会TLE，因此需要选取巧方法解题；
2. 题85是题84的升级版，一个是一维题，另一个是二维题；
3. 纵观这两题的多个解法，我们会发现，解法都会围绕横向扩展、纵向扩展做文章，i.e.,会探索当前点与左右或者上下点的关系，而往往这种题，比较适合用单调栈解题，因为单调栈就是探讨一段连续序列之间的关系.

————————————

参考资料

https://www.cnblogs.com/grandyang/p/4322653.html