引入问题
给你一个数组nums,再给你一大串任意多的区间[i,j]和数字n,叫你对nums数组的区间[i,j],做+n操作,要你最后给出nums数组的值
思路:
对于每一个区间[i,j],使用一个循环,从num[i]开始,到nums[j],每个数字都+n,这样做看上去似乎行得通,但是一旦数组元素的数量非常大,区间[i,j]的跨度非常大,区间的数量非常多,非常容易导致时间超限,那我们如何来进行优化呢?
何为差分数组
差分数组被用来快速对数组某一段区间进行增加或减少操作
假设原nums数组的值为{5,7,6,3,8},计算出差分数组differen,其中differen[i] = nums[i]-nums[i-1],特殊情况differen[0] = nums[0]
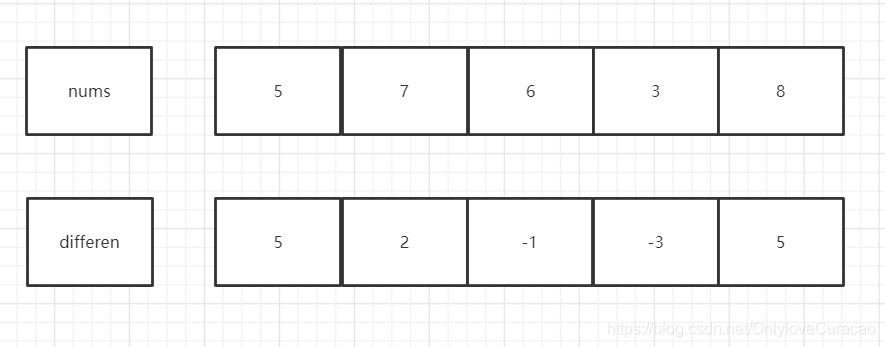
如何由差分数组还原到原数组呢?num[i] = num[i-1] + differen[i],特殊情况:nums[0] = differen[0]
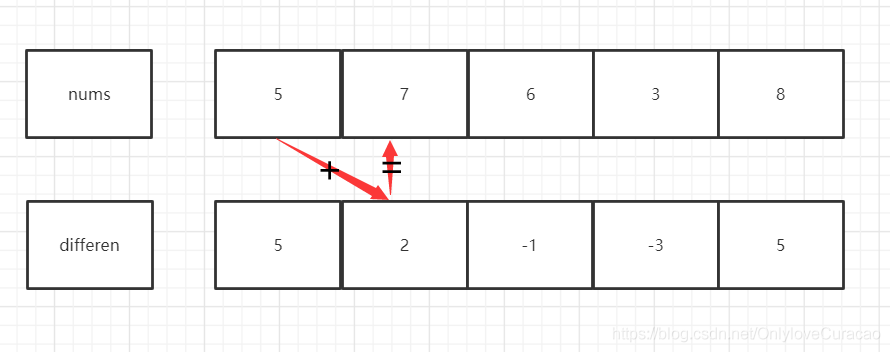
如何使用差分数组对数组的某一块区域做增加或减少的操作呢?
假设区间为[1,3],n为5,我们只需要对differen[1]+5,differen[3+1]-5,就可以了
当我们对differen[1]+5,就意味着我们对nums[1]到最后,都加了5
原因是因为num[1] = num[0] + differen[1],differen[1]加了5,导致num[1]加了5,而num[2] = num[1] + differen[2],导致num[2]也加了5,依次类推,所以我们需要在differen[3+1]-5,保证只有区间[1,3]是加5
航班预订统计
现在我们来看一下leetcode第1109题:航班预订统计
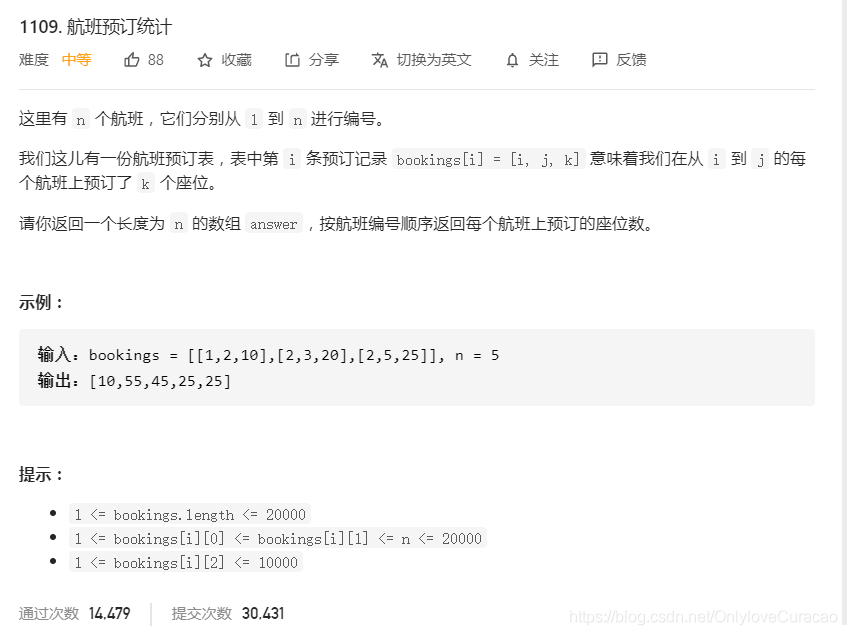
分析题意,不难得出,n为数组大小,原数组所有元素都为0,给出区间,对这个区间做增加操作,刚刚好对应前面的差分数组
以下为参考代码:
class Solution {
public int[] corpFlightBookings(int[][] bookings, int n) {
// 因为原始数组全为0,所以差分数组也全为0
int[] differen = new int[n];
// 对差分数组做区间加法
for(int i=0; i<bookings.length; i++){
differen[bookings[i][0]-1]+=bookings[i][2];
// 如果区间的右部和数组一样大,表示区间中的元素都需要加,不需要做减法截断
if(bookings[i][1] < n){
differen[bookings[i][1]]-=bookings[i][2];
}
}
// 还原原始数组
int[] sum = new int[n];
sum[0] =differen[0];
for(int i=1; i<n; i++){
sum[i] = sum[i-1]+differen[i];
}
return sum;
}
}所有排列中的最大和
我们再来看一下第35场双周赛,第二题:所有排列中的最大和

根据题意进行分析可以得知:本题需要求的是,requests数组中,按照区间中数字出现次数排序,然后将nums数组排序,将nums数组中大的数和区间中出现数字次数多的相乘,即是最后的答案,下面我们拿第三个用例来分析
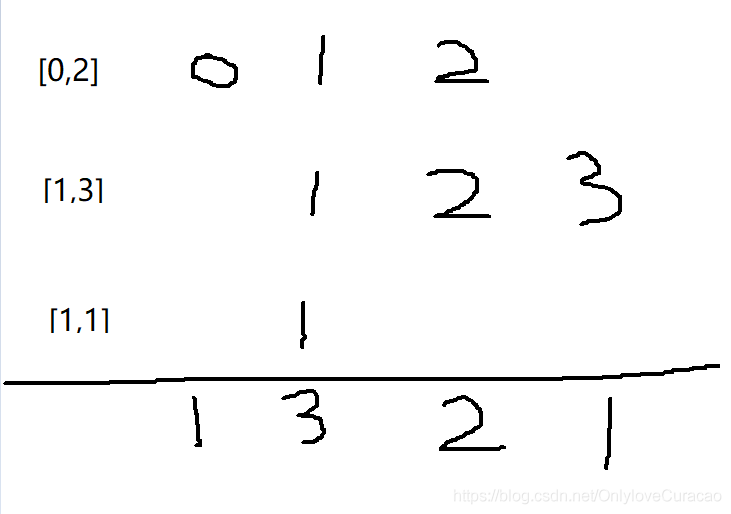

在题目中我们唯一的难点就是,如何快速计算requests中,每个区间中数字出现的次数,刚刚好,我们今天学习了差分数组,正好派上用场,这里我们可以把原始数组当成是全是0,每个区间,都增加1
参考代码:
class Solution {
public int maxSumRangeQuery(int[] nums, int[][] requests) {
int ans = 0;
// 排序数组,为后续乘法做准备
Arrays.sort(nums);
// 创建差分数组
int count[] = new int[nums.length];
int index = 0;
// 使用差分数组进行区间加法
for(int i=0; i<requests.length; i++){
count[requests[i][0]]+=1;
if(requests[i][1]+1 < nums.length){
count[requests[i][1]+1]-=1;
}
}
// 原始数组
int sum[] = new int[nums.length];
// 利用差分数组计算原始数组
sum[0] = count[0];
for(int i=1; i<nums.length; i++){
sum[i] = sum[i-1]+count[i];
}
// 原始数组排序
Arrays.sort(sum);
// 开始计算大小
int sort = nums.length-1;
for(int i=sum.length-1; i>=0; i--){
if(sum[i] == 0){
break;
}
ans+=nums[sort--]*sum[i];
ans = ans%1000000007;
}
return ans;
}
}