一、波动方程简介
在实际工作中,经常涉及求解常微分方程边值问题、偏微分方程边值问题。通常,方程的精确解难以求解,而只能得到求解区域内某些点处解的近似值,即数值解。在数学上,二阶线性偏微分方程分为双曲型、抛物型、椭圆型三种,其中双曲型方程的典型代表是波动方程。当满足合适的边界条件和初始条件时,波动方程是可以求解的。常用的求解方法有分离变量法、行波法、格林函数法、积分变换法等等。其中最为常用的是分离变量法。而当所讨论的问题的边界条件较为复杂时,分离变量法将不再便于计算。因此,对于不易求解解析解的波动方程的数值解的研究和发展具有重要意义。有限差分法是一种较为成熟的数值解法,它的主要思想是将连续的问题离散化。是将每一处导数由有限差分近似公式代替,从而把求解偏微分方程的问题转换成求解代数方程的问题的方法。本文在介绍了有限差分法的基础知识后给出了波动方程及其初始、边界条件的差分格式,列举了一些不同定解条件下的波动方程的数值求解方法及图像。本文将着重探讨波动方程的数值解法
- 波动方程可表述如下,并给出了定解条件:
{
∂
2
u
∂
t
2
−
c
2
∂
2
u
∂
x
2
=
f
(
x
)
,
(
0
≤
x
≤
a
0
,
0
≤
t
≤
t
m
a
x
)
u
(
x
,
t
)
∣
t
=
0
=
R
1
(
x
)
(
0
≤
x
≤
1
)
∂
u
(
x
,
t
)
∂
t
∣
t
=
0
=
R
2
(
x
)
(
0
≤
x
≤
1
)
a
1
u
+
b
1
∂
u
∂
n
=
c
1
(
t
≥
0
)
a
2
u
+
b
2
∂
u
∂
n
=
c
2
(
t
≥
0
)
\begin{cases} {\frac{\partial^2 u}{\partial t^2}-c^2\frac{\partial^2 u}{\partial x^2}=f(x)}, & \text {($0 \leq x \leq a_0,0 \leq t \leq t_{max}$)} \\ {u(x,t)|_{t=0}=R_1(x)} & \text {($0 \leq x \leq 1$)} \\{\frac{\partial u(x,t)}{\partial t}|_{t=0}=R_2(x)} & \text {($0 \leq x \leq 1$)} \\{ a_1u+b_1 \frac{\partial u}{\partial n}=c_1} & \text {($t \geq 0$)} \\{ a_2u+b_2 \frac{\partial u}{\partial n}=c_2} & \text {($t \geq 0$)} \end{cases}
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∂t2∂2u−c2∂x2∂2u=f(x),u(x,t)∣t=0=R1(x)∂t∂u(x,t)∣t=0=R2(x)a1u+b1∂n∂u=c1a2u+b2∂n∂u=c2(0≤x≤a0,0≤t≤tmax)(0≤x≤1)(0≤x≤1)(t≥0)(t≥0)
波动方程可表述如下,并给出在定解条件下的方程组组
二、有限差分法
有限差分法是在采用数值计算方法求解偏微分方程时,将每一处导数由有限差分近似公式代替,从而把求解偏微分方程的问题转换成求解代数方程的问题的方法。有限差分法首先用差分代替微分方程中的微分,将连续变化的变量离散化,从而得到差分方程组的数学形式;继而再求解差分方程组。
其总的思想是用差商代替微商,可用下面的式子表示
d
f
(
x
)
d
x
=
f
(
x
+
h
)
−
f
(
x
)
h
(
向
前
差
商
)
\frac{df(x)}{dx} = \frac{f(x+h)-f(x)}{h}(向前差商)
dxdf(x)=hf(x+h)−f(x)(向前差商)
上面的十字仅仅表示一阶差商同样二阶差商也可以进行类似的表述
∂
2
f
(
x
,
y
)
∂
y
2
=
f
(
x
,
y
+
δ
y
)
−
f
(
x
,
y
−
δ
y
)
−
2
f
(
x
,
y
)
(
δ
y
)
2
\frac{\partial^2 f(x,y)}{\partial y^2} = \frac{f(x,y+ \delta y)-f(x,y – \delta y)-2f(x,y)}{(\delta y)^2}
∂y2∂2f(x,y)=(δy)2f(x,y+δy)−f(x,y−δy)−2f(x,y)
那么波动方程可表示为
∂
u
(
x
,
t
)
∂
t
∣
t
=
0
=
1
τ
(
u
i
1
−
u
i
0
)
\frac{\partial u(x,t)}{\partial t}|_{t=0}=\frac{1}{\tau}(u^1_i-u^0_i)
∂t∂u(x,t)∣t=0=τ1(ui1−ui0)
则初始条件为
u
i
0
=
R
1
(
x
i
)
u^0_i = R_1(x_i)
ui0=R1(xi)
u
i
1
=
R
2
(
x
i
)
u^1_i = R_2(x_i)
ui1=R2(xi)
边界条件为
u
n
=
2
h
C
2
+
4
b
n
+
1
−
b
2
u
n
+
2
2
h
a
2
+
3
b
2
u_n = \frac{2hC_2 + 4b_{n+1} – b_2u_{n+2}}{2ha_2 + 3b_2}
un=2ha2+3b22hC2+4bn+1−b2un+2
三、代码及运行结果
- 本次测试使用了如下定解条件
{
∂
2
u
∂
t
2
−
c
2
∂
2
u
∂
x
2
=
0
,
(
0
≤
x
≤
1
,
t
≥
0
)
u
(
x
,
t
)
∣
t
=
0
=
s
i
n
(
π
x
)
(
0
≤
x
≤
1
)
∂
u
(
x
,
t
)
∂
t
∣
t
=
0
=
0
(
0
≤
x
≤
1
)
u
(
0
,
t
)
=
u
(
1
,
t
)
=
0
(
t
≥
0
)
\begin{cases} {\frac{\partial^2 u}{\partial t^2}-c^2\frac{\partial^2 u}{\partial x^2}=0}, & \text {($0 \leq x \leq 1,t\geq 0$)} \\ {u(x,t)|_{t=0}=sin(\pi x)} & \text {($0 \leq x \leq 1$)} \\{\frac{\partial u(x,t)}{\partial t}|_{t=0}=0} & \text {($0 \leq x \leq 1$)} \\{u(0,t)=u(1,t)=0} & \text {($t \geq 0$)} \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧∂t2∂2u−c2∂x2∂2u=0,u(x,t)∣t=0=sin(πx)∂t∂u(x,t)∣t=0=0u(0,t)=u(1,t)=0(0≤x≤1,t≥0)(0≤x≤1)(0≤x≤1)(t≥0) - 在此用Python实现
import numpy as np
import matplotlib.pyplot as plt
# 初始化
delta_t = 0.02 # 时间步长
delta_x = 0.02 # 控件步长
c = 1 # 波速
tao = c * delta_t / delta_x
u = np.zeros((51, 80))
# 初始条件
for i in range(0, 51):
u[i][0] = np.sin(i * delta_x * np.pi);
u[i][1] = np.sin(i * delta_x * np.pi);
# 边界条件
u[0, :] = 0
u[50, :] = 0
# 迭代
for t in range(1, 79):
for x in range(1, 50):
u[x][t + 1] = 2 * (1 - tao ** 2) * u[x][t] - u[x][t - 1] + tao ** 2 * (u[x - 1][t] + u[x + 1][t])
# 画图
x = np.arange(0, 1.02, 0.02)
for t in range(0, 80, 2):
plt.plot(x, u[:, t], color="r", linewidth=0.8)
plt.xlabel("x/cm")
plt.ylabel("u/cm")
plt.show()
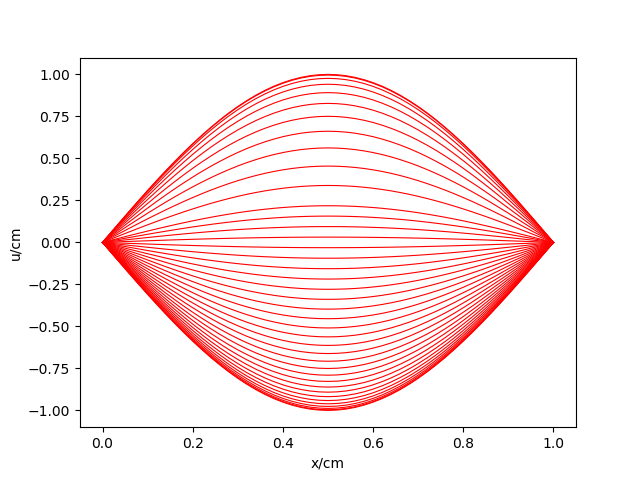
结果如下
可以看出是非常典型的驻波
四、总结
在此主要总结一下本次的心得体会。代码并不复杂,毕竟计算机只是一种工具,在编写的过程中,频繁的错误结果,往往是因为没有正确的把握理论。比如,简单粗暴的套公式,不仅没有真正理解差分方法的本质,而且代码错误率极高。之后返回去理解差分方法之后,效率有所提升,并且也获得了比较满意的结果。“磨刀不误砍柴工”说的就是这个道理了。