
448. 找到所有数组中消失的数字
给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组,数组中的元素一些出现了两次,另一些只出现一次。
找到所有在 [1, n] 范围之间没有出现在数组中的数字。
示例:
输入: [4,3,2,7,8,2,3,1]
输出: [5,6]思路:索引范围为 0 -> (n-1),数字范围为 1 -> n,因此可以用索引i表示数字(i+1)是否出现过, 正好一一对应。
核心问题是每个索引位既要保存原本的数字,又要包含数字(i+1)是否出现过的信息,因此可以巧妙使用正负号来表示,如果(i+1)出现过了,则索引i变为负数,最后看哪些索引是正数就表明对应的数字没出现。
class Solution:
def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
n = len(nums)
for i in range(n):
v = abs(nums[i])
nums[v-1] = - abs(nums[v-1]) # v对应的索引为v-1,将其变为负数
res = [ i+1 for i in range(n) if nums[i] > 0 ]
return res279. 完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.思路:任意的n可以由更小的n得到,注释在代码中:
class Solution:
def numSquares(self, n: int) -> int:
dp = list(range(n+1)) # dp[i]表示和为i的最小完全平方数个数
for i in range(1,n+1):
'''
转移方程如下:
dp[i] = 所有可能中,个数最小的一个,例如:
dp[12] = min(dp[3]+1, dp[8]+1, dp[11]+1)
因为12可以由这些组合得到:3+9,8+4,11+1
'''
dp[i] = min([dp[i-j**2]+1 for j in range(1,int(i**0.5)+1)])
return dp[n]283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。必须在原数组上操作。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]思路:时间复杂度可以做到O(N)。
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
zero_cnt = 0
# 遍历,遇到非零元素即移到前边合适的位置
for i in range(len(nums)):
num = nums[i]
if num == 0:
zero_cnt += 1
else:
nums[i-zero_cnt] = num
# 把后边应该置零的部分全部置零即可
for i in range(len(nums)-zero_cnt,len(nums)):
nums[i] = 0238. 除自身以外数组的乘积
长度为 n 的整数数组 nums,其中 n > 1,返回输出数组 output ,其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。要求不使用除法。
输入: [1,2,3,4] 输出: [24,12,8,6]
思路:从左往右遍历一轮,得到每个索引位置左边所有元素乘积。然后再从右往左,乘以每个索引位置右边的乘积。
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
left_product = 1
res = [] # 保存每个位置左边所有元素的积
for i in range(len(nums)):
res.append(left_product)
left_product *= nums[i]
right_product = 1
for i in range(len(nums)-1,-1,-1):
res[i] *= right_product # 乘上每个位置右边所有元素的积
right_product *= nums[i]
return res739. 每日温度
请根据每日 气温 列表,重新生成一个列表。对应位置的输出为:要想观测到更高的气温,至少需要等待的天数。如果气温在这之后都不会升高,请在该位置用 0 来代替。
例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]
输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
思路:
第一感觉很容易想到对每个元素,遍历后边的元素直到找到第一个大于它的元素,记录索引之差即可。
具体操作时将每个索引放入栈中,然后把栈中元素轮流与列表中下一个元素比较,一旦下一个元素大于栈中元素A,则就找到了A的下一个更高气温,A即可出栈,此时最坏情况下时间复杂度为O(N2),如表中每个元素都相同。
如果观察到如下特点即可优化,即栈中的元素必然是非递增关系,因为如果有递增,则较小的元素就出栈了。因此表中下一个元素与栈中元素比较时,从后往前比较,一旦小于等于某栈中元素即可停止,因为必然也小于栈内前边的元素。这样就避免遍历栈中所有的元素了,时间复杂度O(N)。
class Solution:
def dailyTemperatures(self, T: List[int]) -> List[int]:
cache = []
res = [0]*len(T)
for i in range(len(T)):
while cache and T[i]>T[cache[-1]]: # 从后向前与栈中元素比较
res[cache[-1]] = i-cache[-1]
del cache[-1]
cache.append(i)
return res11. 盛最多水的容器
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
示例:
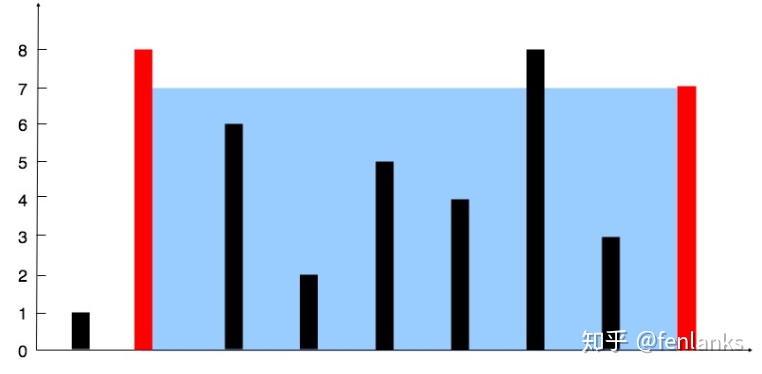
输入:[1,8,6,2,5,4,8,3,7] 输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。思路:
直观方式是遍历数组中所有的两两组合,找到最大的容纳量,时间复杂度为O(N^2^)。进一步优化思路是排除所有不可能的状态,从两边分别向中间靠拢,每次只移动一个边,移动哪边呢?移动更低的那个边,因为容量是(两边的距离*两边里更低的高度),向中间靠拢时,两边的距离是减小的,因此两边中更低的边增加,才有可能得到更大的容量,因此要移动更低的那个边。
class Solution:
def maxArea(self, height: List[int]) -> int:
i_left = 0 # i_left为左边沿的索引
i_right = len(height)-1
capacity = 0
while i_left < i_right:
v_left = height[i_left] # v_left为左边沿的高度
v_right = height[i_right]
new_capacity = (i_right-i_left) * min(v_left, v_right)
capacity = max(capacity, new_capacity)
if v_right > v_left:
i_left += 1
else:
i_right -= 1
return capacity持续更新中。。