对偶理论和灵敏度分析
文章目录
修正单纯形法—矩阵描述和计算
-
修正的目的不是为了方便人的徒手证明,而是为了帮计算机释放内存(人:矩阵的初等行变换;计算机:用矩阵乘法来算,左乘)
-
e.g.
max
z
=
2
x
1
+
3
x
2
+
0
x
3
+
0
x
4
+
0
x
5
,
s
.
t
.
{
x
1
+
2
x
2
+
x
3
=
8
4
x
1
+
x
4
=
16
4
x
2
+
x
5
=
12
x
i
≥
0
\max z=2x_1+3x_2+0x_3+0x_4+0x_5 , ~s.t. \left\{\begin{array}{lc} x_1+2x_2+x_3=8 \\ 4x_1+x_4=16\\ 4x_2+x_5=12\\ x_i\ge 0 \end{array}\right.
maxz=2x1+3x2+0x3+0x4+0x5, s.t.⎩⎪⎪⎨⎪⎪⎧x1+2x2+x3=84x1+x4=164x2+x5=12xi≥0
-
系数矩阵
A
A
A及价值系数
C
C
C,限额系数
b
b
b
A
=
(
P
1
,
P
2
,
P
3
,
P
4
,
P
5
)
=
[
1
2
1
0
0
4
0
0
1
0
0
4
0
0
1
]
,
C
=
(
2
,
3
,
0
,
0
,
0
)
,
b
=
[
8
16
12
]
A=(P_1,P_2,P_3,P_4,P_5)=\left[\begin{array}{ccccc} 1&2&1&0&0\\4&0&0&1&0\\0&4&0&0&1 \end{array}\right], C=(2,3,0,0,0), b=\left[\begin{array}{c} 8\\16\\12 \end{array}\right]
A=(P1,P2,P3,P4,P5)=⎣⎡140204100010001⎦⎤,C=(2,3,0,0,0),b=⎣⎡81612⎦⎤
-
初始可行基
B
0
,
B
0
−
1
B_0,B_0^{-1}
B0,B0−1以及非可行基
N
0
N_0
N0
B
0
=
(
P
3
,
P
4
,
P
5
)
=
[
1
0
0
0
1
0
0
0
1
]
,
B
0
−
1
=
[
1
0
0
0
1
0
0
0
1
]
,
N
0
=
[
1
2
4
0
0
4
]
B_0=(P_3,P_4,P_5)= \left[\begin{array}{ccc} 1&0&0\\0&1&0\\0&0&1 \end{array}\right], B_0^{-1}=\left[\begin{array}{ccc} 1&0&0\\0&1&0\\0&0&1 \end{array}\right], N_0=\left[\begin{array}{ccc} 1&2\\4&0\\0&4 \end{array}\right]
B0=(P3,P4,P5)=⎣⎡100010001⎦⎤,B0−1=⎣⎡100010001⎦⎤,N0=⎣⎡140204⎦⎤
初始基变量
X
B
0
=
[
x
3
x
4
x
5
]
X_{B_0}=\left[\begin{array}{c} x_3\\x_4\\x_5 \end{array}\right]
XB0=⎣⎡x3x4x5⎦⎤,系数
C
B
0
=
(
0
,
0
,
0
)
C_{B_0}=(0,0,0)
CB0=(0,0,0);非基变量
X
N
0
=
[
x
1
x
2
]
X_{N_0}=\left[\begin{array}{ccc} x_1\\x_2 \end{array}\right]
XN0=[x1x2],系数
C
N
0
=
(
2
,
3
)
C_{N_0}=(2,3)
CN0=(2,3)
-
非基变量检验数
σ
N
0
=
C
N
0
−
C
B
0
B
0
−
1
N
0
=
(
2
,
3
)
−
(
0
,
0
,
0
)
[
1
0
0
0
1
0
0
0
1
]
[
1
2
4
0
0
4
]
=
(
2
,
3
)
\sigma_{N_0}=C_{N_0}-C_{B_0}B_0^{-1}N_0=(2,3)-(0,0,0)\left[\begin{array}{ccc} 1&0&0\\0&1&0\\0&0&1 \end{array}\right]\left[\begin{array}{ccc} 1&2\\4&0\\0&4 \end{array}\right]=(2,3)
σN0=CN0−CB0B0−1N0=(2,3)−(0,0,0)⎣⎡100010001⎦⎤⎣⎡140204⎦⎤=(2,3)
由此确定x
2
x_2
x2为换入变量
-
计算
θ
\theta
θ
θ
=
min
{
(
B
0
−
1
b
)
i
(
B
0
−
1
P
2
)
i
∣
B
0
−
1
P
2
>
0
}
=
min
(
8
2
,
−
,
12
4
)
=
3
\theta=\min\left\{\left.\frac{(B_0^{-1}b)_i}{(B_0^{-1}P_2)_i}\right|B_0^{-1}P_2>0\right\} =\min(\frac{8}{2},-,\frac{12}{4})=3
θ=min{(B0−1P2)i(B0−1b)i∣∣∣∣B0−1P2>0}=min(28,−,412)=3
对应的换出变量为x
5
x_5
x5
-
求出新的可行基
B
1
,
B
1
−
1
B_1,B_1^{-1}
B1,B1−1以及非可行基
N
1
N_1
N1
B
1
=
[
1
0
2
0
1
0
0
0
4
]
,
B
1
−
1
=
[
1
0
−
1
/
2
0
1
0
0
0
1
/
4
]
,
N
1
=
[
1
0
4
0
0
1
]
B_1=\left[\begin{array}{ccc} 1&0&2\\0&1&0\\0&0&4 \end{array}\right], B_1^{-1}=\left[\begin{array}{ccc} 1&0&-1/2\\0&1&0\\0&0&1/4 \end{array}\right], N_1=\left[\begin{array}{ccc} 1&0\\4&0\\0&1 \end{array}\right]
B1=⎣⎡100010204⎦⎤,B1−1=⎣⎡100010−1/201/4⎦⎤,N1=⎣⎡140001⎦⎤
新基变量X
B
1
=
[
x
3
x
4
x
2
]
X_{B_1}=\left[\begin{array}{ccc} x_3\\x_4\\x_2 \end{array}\right]
XB1=⎣⎡x3x4x2⎦⎤,系数
C
B
1
=
(
0
,
0
,
3
)
C_{B_1}=(0,0,3)
CB1=(0,0,3);非基变量
X
N
1
=
[
x
1
x
5
]
X_{N_1}=\left[\begin{array}{ccc} x_1\\x_5 \end{array}\right]
XN1=[x1x5],系数
C
N
1
=
(
2
,
0
)
C_{N_1}=(2,0)
CN1=(2,0)
-
重复以上步骤,直到所有非基变量检验数均小于0。经过多次迭代之后,最后得到最优解
X
∗
=
[
x
1
x
5
x
2
]
=
B
3
−
1
b
=
[
4
4
2
]
,
z
∗
=
C
B
3
B
3
−
1
b
=
(
2
,
0
,
3
)
[
4
4
2
]
=
14
X^*=\left[\begin{array}{ccccc} x_1\\x_5\\x_2 \end{array}\right]=B_3^{-1}b =\left[\begin{array}{ccccc} 4\\4\\2 \end{array}\right], z^*=C_{B_3}B_3^{-1}b=(2,0,3)\left[\begin{array}{ccccc} 4\\4\\2 \end{array}\right]=14
X∗=⎣⎡x1x5x2⎦⎤=B3−1b=⎣⎡442⎦⎤,z∗=CB3B3−1b=(2,0,3)⎣⎡442⎦⎤=14
注:矩阵求逆可使用伴随矩阵求解或者初等行变换求解。求出的最优解需综合非基变量(都是0)得到最终的最优解
X
∗
=
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
)
T
=
(
4
,
2
,
0
,
0
,
5
)
T
X^*=(x_1,x_2,x_3,x_4,x_5)^T=(4,2,0,0,5)^T
X∗=(x1,x2,x3,x4,x5)T=(4,2,0,0,5)T
-
对偶问题的提出
-
来源于生产优化问题
-
某工厂A生产甲、乙两种产品,消耗煤、电、油三种资源,相关数据如下表
甲 乙 资源限制 煤 9 4 360 电 4 5 200 油 3 10 300 单位利润 7 12 求总收入最大的生产计划方案。
-
原问题的线性规划(LP)为
max
z
=
7
x
1
+
12
x
2
s
.
t
.
{
9
x
1
+
4
x
2
≤
360
4
x
1
+
5
x
2
≤
200
3
x
1
+
10
x
2
≤
300
x
1
,
x
2
≥
0
\begin{array}{l} \max z=7x_1+12x_2\\ s.t.\left\{\begin{array}{l} 9x_1+4x_2\le 360\\ 4x_1+5x_2\le 200\\ 3x_1+10x_2\le 300\\ x_1,x_2\ge 0 \end{array}\right. \end{array}
maxz=7x1+12x2s.t.⎩⎪⎪⎨⎪⎪⎧9x1+4x2≤3604x1+5x2≤2003x1+10x2≤300x1,x2≥0
-
现考虑对偶问题,加入工厂B想要直接收购工厂A的所有煤电油,则需要给三种资源报价,并且满足工厂A愿意出让资源的条件,即让工厂A获得不低于自己制造产品的收入。不妨设三种资源的报价是
y
i
,
i
=
1
,
2
,
3
y_i,i=1,2,3
yi,i=1,2,3
-
收购工厂A的全部三种资源的总成本是
360
y
1
+
200
y
2
+
300
y
3
360y_1+200y_2+300y_3
360y1+200y2+300y3,总成本应该最低
min
w
=
360
y
1
+
200
y
2
+
300
y
3
\min w=360y_1+200y_2+300y_3
minw=360y1+200y2+300y3
-
工厂A把足够制造一个甲产品的资源卖掉,获得的收入需要保证不低于自己制造时的单位利润。对于乙产品同理
9
y
1
+
4
y
2
+
3
y
3
≥
7
4
y
1
+
5
y
1
+
12
y
3
≥
12
9y_1+4y_2+3y_3\ge 7\\ 4y_1+5y_1+12y_3\ge 12
9y1+4y2+3y3≥74y1+5y1+12y3≥12
-
由此可以得到该线性规划的对偶问题(DLP)为
min
w
=
360
y
1
+
200
y
2
+
300
y
3
s
.
t
.
{
9
y
1
+
4
y
2
+
3
y
3
≥
7
4
y
1
+
5
y
1
+
12
y
3
≥
12
y
1
,
y
2
,
y
3
≥
0
\begin{array}{l} \min w=360y_1+200y_2+300y_3\\ s.t.\left\{\begin{array}{l} 9y_1+4y_2+3y_3\ge 7\\ 4y_1+5y_1+12y_3\ge 12\\ y_1,y_2,y_3\ge 0 \end{array}\right. \end{array}
minw=360y1+200y2+300y3s.t.⎩⎨⎧9y1+4y2+3y3≥74y1+5y1+12y3≥12y1,y2,y3≥0
-
-
-
当一对对偶线性规划问题都有可行解时,对偶问题的最优目标值与原始问题的最优目标值相等
-
上述问题的抽象
LP DLP min
z
=
c
x
s
.
t
.
{
A
x
≤
b
x
≥
0
\begin{array}{l}\min z=cx\\s.t.\left\{\begin{array}{l}Ax\le b\\x\ge 0\end{array}\right.\end{array}
minz=cxs.t.{Ax≤bx≥0max
w
=
b
T
x
s
.
t
.
{
A
T
y
≥
c
T
y
≥
0
\begin{array}{l}\max w=b^Tx\\s.t.\left\{\begin{array}{l}A^Ty\ge c^T\\y\ge 0\end{array}\right.\end{array}
maxw=bTxs.t.{ATy≥cTy≥0
原问题与对偶问题转化
-
由拉格朗日乘数法和KKT定理可知,广义拉格朗日乘子是作用在约束方程上的,所以这就给了我们原问题与对偶问题相互转化的角度与对应关系

- 明确目标,是
min
→
max
\min\to\max
min→max还是max
→
min
\max\to\min
max→min,从而确定表格从左向右看还是从右向左看 - 由约束条件确定变量,变量确定约束
- 明确目标,是
| 原问题 | 对偶问题 |
|---|---|
|
max z = 2 x 1 + 3 x 2 − 5 x 3 + x 4 s . t . { x 1 + x 2 − 3 x 3 + x 4 ≥ 5 2 x 1 + 2 x 3 − x 4 ≤ 4 x 2 + x 3 + x 4 = 6 x 1 ≤ 0 , x 2 , x 3 ≥ 0 , x 4 无约束 \begin{array}{l}\max z=2x_1+3x_2-5x_3+x_4\\s.t.\left\{\begin{array}{l}x_1+x_2-3x_3+x_4\ge 5\\2x_1+2x_3-x_4\le 4\\x_2+x_3+x_4=6\\x_1\le 0,x_2,x_3\ge 0,x_4\text{无约束}\end{array}\right.\end{array} maxz=2x1+3x2−5x3+x4s.t.⎩⎪⎪⎨⎪⎪⎧x1+x2−3x3+x4≥52x1+2x3−x4≤4x2+x3+x4=6x1≤0,x2,x3≥0,x4无约束 |
min w = 5 y 1 + 4 y 2 + 6 y 3 s . t . { y 1 + 2 y 2 ≤ 2 y 1 + y 3 ≥ 3 − 3 y 1 + 2 y 2 + y 3 ≥ − 5 y 1 − y 2 + y 3 = 1 y 1 ≤ 0 , y 2 ≥ 0 , y 3 无约束 \begin{array}{l}\min w=5y_1+4y_2+6y_3\\s.t.\left\{\begin{array}{l}y_1+2y_2\le 2\\y_1+y_3\ge 3\\-3y_1+2y_2+y_3\ge -5\\y_1-y_2+y_3=1\\y_1\le 0,y_2\ge 0,y_3\text{无约束}\end{array}\right.\end{array} minw=5y1+4y2+6y3s.t.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧y1+2y2≤2y1+y3≥3−3y1+2y2+y3≥−5y1−y2+y3=1y1≤0,y2≥0,y3无约束 |
|
min z = 2 x 1 + 3 x 2 − 5 x 3 + x 4 s . t . { x 1 + x 2 − 3 x 3 + x 4 ≥ 5 2 x 1 + 2 x 3 − x 4 ≤ 4 x 2 + x 3 + x 4 = 6 x 1 ≤ 0 , x 2 , x 3 ≥ 0 , x 4 无约束 \begin{array}{l}\min z=2x_1+3x_2-5x_3+x_4\\s.t.\left\{\begin{array}{l}x_1+x_2-3x_3+x_4\ge 5\\2x_1+2x_3-x_4\le 4\\x_2+x_3+x_4=6\\x_1\le 0,x_2,x_3\ge 0,x_4\text{无约束}\end{array}\right.\end{array} minz=2x1+3x2−5x3+x4s.t.⎩⎪⎪⎨⎪⎪⎧x1+x2−3x3+x4≥52x1+2x3−x4≤4x2+x3+x4=6x1≤0,x2,x3≥0,x4无约束 |
max w = 5 y 1 + 4 y 2 + 6 y 3 s . t . { y 1 + 2 y 2 ≥ 2 y 1 + y 3 ≤ 3 − 3 y 1 + 2 y 2 + y 3 ≤ − 5 y 1 − y 2 + y 3 = 1 y 1 ≥ 0 , y 2 ≤ 0 , y 3 无约束 \begin{array}{l}\max w=5y_1+4y_2+6y_3\\s.t.\left\{\begin{array}{l}y_1+2y_2\ge 2\\y_1+y_3\le 3\\-3y_1+2y_2+y_3\le -5\\y_1-y_2+y_3=1\\y_1\ge 0,y_2\le 0,y_3\text{无约束}\end{array}\right.\end{array} maxw=5y1+4y2+6y3s.t.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧y1+2y2≥2y1+y3≤3−3y1+2y2+y3≤−5y1−y2+y3=1y1≥0,y2≤0,y3无约束 |
- 注意以上两个问题的区别
设原问题是
max
z
=
C
X
;
A
X
≤
b
;
X
≥
0
\max z=CX;AX\le b;X\ge 0
maxz=CX;AX≤b;X≥0;对偶问题是
min
w
=
Y
b
;
Y
A
≥
C
;
Y
≥
0
\min w=Yb;YA\ge C;Y\ge 0
minw=Yb;YA≥C;Y≥0
-
对称性:对偶问题的对偶是原问题
-
弱对偶性:若
X
‾
\overline{X}
X是原问题的可行解,
Y
‾
\overline{Y}
Y是对偶问题的可行解,则存在
C
X
‾
≤
Y
‾
b
C\overline{X}\le\overline{Y}b
CX≤Yb
{
A
X
‾
≤
b
⇒
Y
‾
A
X
‾
≤
Y
‾
b
Y
‾
A
≥
C
⇒
Y
‾
A
X
‾
≥
C
X
‾
⇒
C
X
‾
≤
Y
‾
b
\left\{\begin{array}{l} A\overline{X}\le b\Rightarrow \overline{Y}A\overline{X}\le\overline{Y}b\\ \overline{Y}A\ge C\Rightarrow \overline{Y}A\overline{X}\ge C\overline{X} \end{array}\right. \Rightarrow C\overline{X}\le\overline{Y}b
{AX≤b⇒YAX≤YbYA≥C⇒YAX≥CX⇒CX≤Yb
-
无界性:若原问题(对偶问题)为无界解,则其对偶问题(原问题)无可行解
-
可行解是最优解时的性质:设
X
^
\hat{X}
X^是原问题的可行解,
Y
^
\hat{Y}
Y^是对偶问题的可行解,当
C
X
^
=
Y
^
b
C\hat{X}=\hat{Y}b
CX^=Y^b时,
X
^
,
Y
^
\hat{X},\hat{Y}
X^,Y^是最优解
Y
‾
b
≥
C
X
^
=
Y
^
b
⇒
Y
^
是使目标函数取值最小的可行解
\overline{Y}b\ge C\hat{X}=\hat{Y}b\Rightarrow\hat{Y}\text{是使目标函数取值最小的可行解}
Yb≥CX^=Y^b⇒Y^是使目标函数取值最小的可行解
-
对偶定理:若原问题有最优解,那么对偶问题也有最优解,且目标函数值相等
X
^
\hat{X}
X^是原问题的最优解
⇒
\Rightarrow
⇒
C
−
C
B
B
−
1
A
≤
0
C-C_BB^{-1}A\le 0
C−CBB−1A≤0,因此可以得到存在
Y
^
=
C
B
B
−
1
\hat{Y}=C_BB^{-1}
Y^=CBB−1使得
Y
^
A
≥
C
\hat{Y}A\ge C
Y^A≥C,即
y
^
\hat{y}
y^是对偶问题的可行解,目标函数的取值分别为
w
=
Y
^
b
=
C
B
B
−
1
b
z
=
C
X
^
=
C
B
B
−
1
b
w=\hat{Y}b=C_BB^{-1}b\\ z=C\hat{X}=C_BB^{-1}b
w=Y^b=CBB−1bz=CX^=CBB−1b
于是可以得到Y
^
b
=
C
X
^
\hat{Y}b=C\hat{X}
Y^b=CX^,因此
Y
^
\hat{Y}
Y^是对偶问题的最优解
-
互补松弛性:若
X
^
,
Y
^
\hat{X},\hat{Y}
X^,Y^分别是原问题和对偶问题的可行解,那么
Y
^
X
S
=
0
\hat{Y}X_S=0
Y^XS=0和
Y
S
X
^
=
0
Y_S\hat{X}=0
YSX^=0当且仅当
X
^
,
Y
^
\hat{X},\hat{Y}
X^,Y^为最优解
-
对偶问题的最优解就是原问题的松弛变量的检验数的负值
对偶问题最优解的经济意义——影子价格
- 意义一定要在特定背景下讨论
| 原问题 | 对偶问题 |
|---|---|
|
max z = 7 x 1 + 12 x 2 s . t . { 9 x 1 + 4 x 2 ≤ 360 4 x 1 + 5 x 2 ≤ 200 3 x 1 + 10 x 2 ≤ 300 x 1 , x 2 ≥ 0 \begin{array}{l}\max z=7x_1+12x_2\\s.t.\left\{\begin{array}{l}9x_1+4x_2\le 360\\4x_1+5x_2\le 200\\3x_1+10x_2\le 300\\x_1,x_2\ge 0\end{array}\right.\end{array} maxz=7x1+12x2s.t.⎩⎪⎪⎨⎪⎪⎧9x1+4x2≤3604x1+5x2≤2003x1+10x2≤300x1,x2≥0 |
min w = 360 y 1 + 200 y 2 + 300 y 3 s . t . { 9 y 1 + 4 y 2 + 3 y 3 ≥ 7 4 y 1 + 5 y 2 + 10 y 3 ≥ 12 y 1 , y 2 , y 3 ≥ 0 \begin{array}{l}\min w=360y_1+200y_2+300y_3\\s.t.\left\{\begin{array}{l}9y_1+4y_2+3y_3\ge 7\\4y_1+5y_2+10y_3\ge 12\\y_1,y_2,y_3\ge 0\end{array}\right.\end{array} minw=360y1+200y2+300y3s.t.⎩⎨⎧9y1+4y2+3y3≥74y1+5y2+10y3≥12y1,y2,y3≥0 |
- 对偶问题最优解的经济意义是原问题的资源的影子价格,在数学上的表示为
C
B
B
−
1
C_BB^{-1}
CBB−1(在原问题的单纯形表终表上可以直接看出,即松弛变量的检验数的相反数) - 原问题的影子价格:当对应资源的限制每增加一个单位(假设其他资源不变),引起的卖方总收入的增加(即卖家的内控价格)
- 影子价格反映了资源对目标函数的边际贡献,即资源转化成经济效益的效率
- 影子价格反映了资源的稀缺程度
- 影子价格=0:表示这种资源有剩余;
- 影子价格>0:表示这种资源用尽了,没剩余,且大于0的程度越高,其价值转化率越高,我们更加关注影子价格更高的资源
- 影子价格反映了资源的边际使用价值
对偶问题约束项的经济意义——生产产品的机会成本
-
机会成本:利用一定的时间或资源生产一种商品时,而失去的利用这些资源生产其他最佳替代品的机会
原问题 对偶问题 max
z
=
c
1
x
1
+
⋯
+
c
n
x
n
s
.
t
.
{
a
11
x
1
+
⋯
+
a
1
n
x
n
≤
b
1
a
21
x
1
+
⋯
+
a
2
n
x
n
≤
b
2
⋮
a
m
1
x
1
+
⋯
+
a
m
n
x
n
≤
b
m
x
i
≥
0
\begin{array}{l}\max z=c_1x_1+\cdots+c_nx_n\\s.t.\left\{\begin{array}{l}a_{11}x_1+\cdots+a_{1n}x_n\le b_1\\a_{21}x_1+\cdots+a_{2n}x_n\le b_2\\\vdots\\a_{m1}x_1+\cdots+a_{mn}x_n\le b_m\\x_i\ge 0\end{array}\right.\end{array}
maxz=c1x1+⋯+cnxns.t.⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧a11x1+⋯+a1nxn≤b1a21x1+⋯+a2nxn≤b2⋮am1x1+⋯+amnxn≤bmxi≥0min
w
=
b
1
y
1
+
⋯
+
b
m
y
m
s
.
t
.
{
a
11
y
1
+
⋯
+
a
m
1
y
m
≥
c
1
a
12
y
1
+
⋯
+
a
m
2
y
m
≥
c
2
⋮
a
1
n
y
1
+
⋯
+
a
m
n
y
m
≥
c
n
y
i
≥
0
\begin{array}{l}\min w=b_1y_1+\cdots+b_my_m\\s.t.\left\{\begin{array}{l}a_{11}y_1+\cdots+a_{m1}y_m\ge c_1\\a_{12}y_1+\cdots+a_{m2}y_m\ge c_2\\\vdots\\a_{1n}y_1+\cdots+a_{mn}y_m\ge c_n\\y_i\ge 0\end{array}\right.\end{array}
minw=b1y1+⋯+bmyms.t.⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧a11y1+⋯+am1ym≥c1a12y1+⋯+am2ym≥c2⋮a1ny1+⋯+amnym≥cnyi≥0 -
a
11
y
1
+
⋯
+
a
m
1
y
m
a_{11}y_1+\cdots+a_{m1}y_m
a11y1+⋯+am1ym表示生产一个产品1所需要的的资源的价值
-
厂商对于现有资源有两个选择:要么是用于生产,将产品卖出去;要么是不生产,直接把资源卖出去。
- 一方面,如果将这些资源投入产品,一旦彻底失败,我们要承担的损失(试错成本)
- 另一方面,如果我们考虑承担机会成本,那么至少应该满足利用这些资源生产产品后再卖出所获得的利润不低于直接出售资源的利润,这样我们才会考虑试错
对偶问题松弛变量的经济意义——生产产品的差额成本
化标准型
⇒
min
w
=
b
1
y
1
+
⋯
+
b
m
y
m
s
.
t
.
{
a
11
y
1
+
⋯
+
a
m
1
y
m
−
y
m
+
1
=
c
1
a
12
y
1
+
⋯
+
a
m
2
y
m
−
y
m
+
2
=
c
2
⋮
a
1
n
y
1
+
⋯
+
a
m
n
y
m
−
y
m
+
n
=
c
n
y
i
≥
0
\text{化标准型}\Rightarrow \begin{array}{l} \min w=b_1y_1+\cdots+b_my_m\\ s.t.\left\{\begin{array}{l} a_{11}y_1+\cdots+a_{m1}y_m-y_{m+1}= c_1\\ a_{12}y_1+\cdots+a_{m2}y_m-y_{m+2}= c_2\\ \vdots\\ a_{1n}y_1+\cdots+a_{mn}y_m-y_{m+n}= c_n\\ y_i\ge 0 \end{array}\right. \end{array}
化标准型⇒minw=b1y1+⋯+bmyms.t.⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧a11y1+⋯+am1ym−ym+1=c1a12y1+⋯+am2ym−ym+2=c2⋮a1ny1+⋯+amnym−ym+n=cnyi≥0
-
引入的剩余变量姑且理解为广义的松弛变量
-
a
11
y
1
+
⋯
+
a
m
1
y
m
a_{11}y_1+\cdots+a_{m1}y_m
a11y1+⋯+am1ym表示生产一个产品1所需要的的资源的价值;
c
i
c_i
ci表示生产一个产品的单位利润
-
y
m
+
i
y_{m+i}
ym+i表示生产一个产品
i
i
i的机会成本减去产品
i
i
i的单位利润
⇒
\Rightarrow
⇒差额成本
-
>
0
>0
>0:生产产品的机会成本大于利润,因此不考虑生产产品i
i
i,不进行试错,而是直接把相应资源卖出去 -
<
0
<0
<0:生产产品的机会成本小于利润,因此考虑生产产品i
i
i,尝试获得更高的收入 -
=
0
=0
=0:临界情况,随缘看,但一般考虑时间安全等因素可能会直接将资源卖掉
-
-
在利润最大化的生产计划中
- 影子价格大于0的资源是没有剩余的
- 有剩余的资源的影子价格等于0
- 机会成本大于利润的产品(差额成本
>
0
>0
>0的产品)不安排生产 - 考虑安排生产的产品的机会成本
≤
\le
≤利润 - 已经开始生产的产品(已经在生产线上的产品)的机会成本一定等于利润(只有两个选择,继续生产或者停止,而目前的状态是已经在生产,因此一旦停产,代价就是利润,这便是对应的机会成本)
对偶单纯形法
-
本质:单纯形法,在某些具体问题中有求简的思想,是结合对偶性质所引出来的方法,切不可理解为“求解对偶问题时使用的单纯形法”
-
往往我们在求解规划问题时,一般先使用单纯形法,到了某个特定的时候(一般是终表)才会接着开始用对偶单纯形法
-
单纯形法:在保证可行性(
B
−
1
b
≥
0
B^{-1}b\ge 0
B−1b≥0)的前提下,通过迭代运算,改善解的最优性(使得
σ
i
=
c
i
−
C
B
B
−
1
P
i
≤
0
\sigma_i=c_i-C_BB^{-1}P_i\le 0
σi=ci−CBB−1Pi≤0),从而找到所需的最优解
- 化标准型,使得
b
≥
0
⇒
B
−
1
b
≥
0
b\ge 0\Rightarrow B^{-1}b\ge 0
b≥0⇒B−1b≥0 - 通过看
σ
i
\sigma_i
σi,找到进基变量 - 通过
θ
\theta
θ比值,找到退基变量 - 换基,迭代运算,直到所有的
σ
i
≤
0
\sigma_i\le 0
σi≤0
- 化标准型,使得
-
对偶单纯形法(保证是求
max
\max
max):在保证最优性(
σ
i
=
c
i
−
C
B
B
−
1
P
i
≤
0
\sigma_i=c_i-C_BB^{-1}P_i\le 0
σi=ci−CBB−1Pi≤0,一般在单纯形表终表时使用)的前提下,通过迭代运算,改善可行性(使得
B
−
1
b
≥
0
B^{-1}b\ge 0
B−1b≥0),从而找到所需的最优解
- 保证初始可行基的最优性,即所有的
σ
i
≤
0
\sigma_i\le 0
σi≤0 - 通过看
B
−
1
b
B^{-1}b
B−1b,找到退基的变量。若都是非负的,则此时已经是最优解;若存在至少一个负数,则找出负数中最小的数(绝对值最大的)对应的变量作为退基变量 - 观察退基变量所在行的所有系数
a
i
j
a_{ij}
aij,若所有的a
i
j
≥
0
a_{ij}\ge 0
aij≥0,则无可行解,否则进入下一步找进基变量 - 通过
θ
\theta
θ比值(检验数除以退基变量所在行的系数),找到进基的变量,将大于0的θ
\theta
θ中最小值对应的变量作为进基变量 - 换基,迭代运算,直到所有的
B
−
1
b
≥
0
B^{-1}b\ge 0
B−1b≥0
- 保证初始可行基的最优性,即所有的
-
题目不要求的话一般还是使用大M法,对偶单纯形法一般只在题目特殊要求或者不满足可行性时使用
灵敏度分析
-
着眼于一个范围不大的局域
-
灵敏度分析分为两步
- 保证引入的
Δ
\Delta
Δ变量的新问题与原问题高度相同(可行域长得基本一样;解的相对位置不发生改变。即保持新问题的最优基不变) - 研究引入
Δ
\Delta
Δ后对x
∗
,
z
∗
x^*,z^*
x∗,z∗的影响
- 保证引入的
-
限额系数
b
b
b变化时第
r
r
r种资源由原来的
b
r
b_r
br变为
b
r
+
Δ
b
r
b_r+\Delta b_r
br+Δbr,要使原最优解不变,只需
B
−
1
b
‾
=
B
−
1
(
−
1
+
[
0
⋮
Δ
b
r
⋮
0
]
)
≥
0
B^{-1}\overline{b}=B^{-1}(-1+ \left[\begin{array}{c} 0\\\vdots\\\Delta b_r\\\vdots\\0 \end{array}\right]) \ge 0
B−1b=B−1(−1+⎣⎢⎢⎢⎢⎢⎢⎡0⋮Δbr⋮0⎦⎥⎥⎥⎥⎥⎥⎤)≥0
然后解出Δ
b
r
\Delta b_r
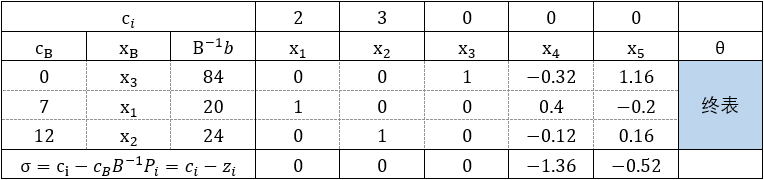
Δbr范围即可。以煤电油问题为例:
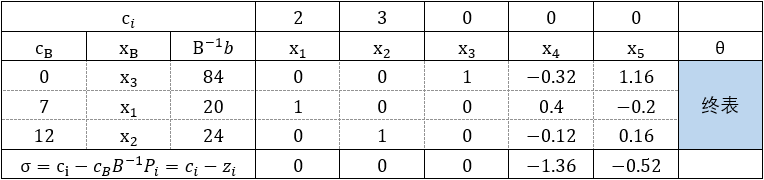
B
−
1
b
‾
=
B
−
1
b
+
B
−
1
[
0
0
Δ
b
3
]
=
[
84
20
24
]
+
[
1
−
0.32
1.16
0
0.4
−
0.2
0
−
0.12
0.16
]
[
0
0
Δ
b
3
]
≥
0
⇒
{
84
+
1.16
Δ
b
3
≥
0
20
−
0.2
Δ
b
3
≥
0
24
+
0.16
Δ
b
3
≥
0
⇒
−
72
≤
Δ
b
3
≤
100
B^{-1}\overline{b}=B^{-1}b+B^{-1} \left[\begin{array}{c} 0\\0\\\Delta b_3 \end{array}\right] =\left[\begin{array}{c} 84\\20\\24 \end{array}\right] +\left[\begin{array}{ccc} 1&-0.32&1.16\\ 0&0.4&-0.2\\ 0&-0.12&0.16 \end{array}\right]\left[\begin{array}{c} 0\\0\\\Delta b_3 \end{array}\right] \ge 0\\ \Rightarrow \left\{\begin{array}{lcl} 84+1.16\Delta b_3 &\ge&0\\ 20-0.2\Delta b_3 &\ge&0\\ 24+0.16\Delta b_3 &\ge&0 \end{array}\right. \Rightarrow -72\le\Delta b_3\le 100
B−1b=B−1b+B−1⎣⎡00Δb3⎦⎤=⎣⎡842024⎦⎤+⎣⎡100−0.320.4−0.121.16−0.20.16⎦⎤⎣⎡00Δb3⎦⎤≥0⇒⎩⎨⎧84+1.16Δb320−0.2Δb324+0.16Δb3≥≥≥000⇒−72≤Δb3≤100
在保证最优基不变的前提下,限额系数b
3
b_3
b3的变化范围是
−
72
≤
Δ
b
3
≤
100
-72\le \Delta b_3\le 100
−72≤Δb3≤100
-
价值系数
c
j
c_j
cj变化为
c
j
+
Δ
c
j
c_j+\Delta c_j
cj+Δcj时,它只对
σ
\sigma
σ产生影响,
σ
j
‾
=
c
j
‾
−
c
B
‾
B
−
1
P
j
\overline{\sigma_j}=\overline{c_j}-\overline{c_B}B^{-1}P_j
σj=cj−cBB−1Pj,观察终表
-
当
x
j
x_j
xj是非基变量,
c
j
c_j
cj是非基变量的系数,它只对自己的
σ
\sigma
σ产生了过影响,故只需介入下阿不等式即可
σ
j
‾
=
c
j
‾
−
c
B
B
−
1
P
j
=
(
c
j
+
Δ
c
j
)
−
c
B
B
−
1
P
j
≤
0
\overline{\sigma{j}}=\overline{c_j}-c_BB^{-1}P_j=(c_j+\Delta c_j)-c_BB^{-1}P_j\le 0
σj=cj−cBB−1Pj=(cj+Δcj)−cBB−1Pj≤0
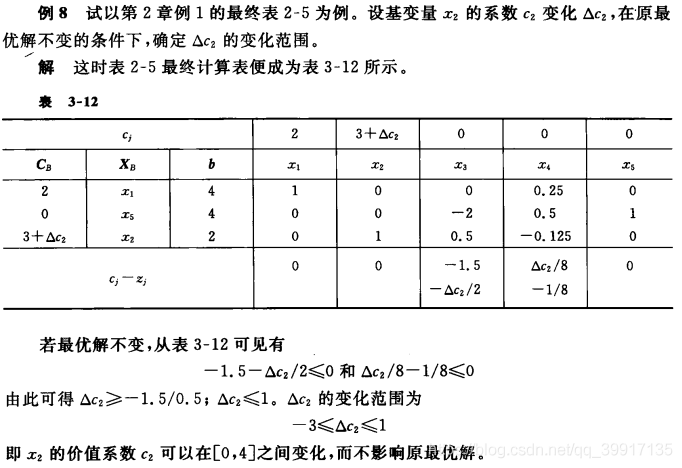
-
当
x
j
x_j
xj是基变量,
c
j
c_j
cj是基变量的系数,对所有的
σ
\sigma
σ都产生影响,故只需解如下不等式组即可
σ
i
‾
=
c
i
−
c
B
‾
B
−
1
P
i
≤
0
,
i
=
1
,
⋯
,
n
\overline{\sigma_i}=c_i-\overline{c_B}B^{-1}P_i\le 0,i=1,\cdots,n
σi=ci−cBB−1Pi≤0,i=1,⋯,n
-
-
技术系数
a
i
j
a_{ij}
aij变化为
a
i
j
+
Δ
a
i
j
a_{ij}+\Delta a_{ij}
aij+Δaij时
-
若保证
A
A
A的列数不变,用变化后的
P
j
‾
\overline{P_j}
Pj替换
P
j
P_j
Pj,从初表开始常规运算,然后令
σ
j
‾
=
c
j
−
c
B
B
−
1
P
j
‾
≤
0
\overline{\sigma_j}=c_j-c_BB^{-1}\overline{P_j}\le 0
σj=cj−cBB−1Pj≤0即可
-
若
A
A
A的列数发生变化,意味着安排生产了一种新产品。计算新增列对应的检验数
σ
n
+
1
=
c
n
+
1
−
c
B
B
−
1
P
n
+
1
\sigma_{n+1}=c_{n+1}-c_BB^{-1}P_{n+1}
σn+1=cn+1−cBB−1Pn+1,若
σ
n
+
1
>
0
\sigma_{n+1}>0
σn+1>0,则投产有利,考虑生产该产品;若
σ
n
+
1
<
0
\sigma{n+1}<0
σn+1<0,则投产无利,不考虑生产
-
若碰到原问题和对偶问题均为非可行解时,就需要引进人工变量后重新求解
替换后的原问题终表 对偶问题终表 如何进行下一步 可行解 可行解 表中的解仍是最优解 可行解 非可行解 继续用单纯形法计算 非可行解 可行解 用对偶单纯形法计算
-