圆周率的计算

    正方形内部有一个内切圆，则正方形和内切圆的面积之比为：（2r)^2/Πr^2 = 4/Π

    因此，圆周率的计算问题转化为计算正方形的面积和其内切圆的面积的问题。

方法

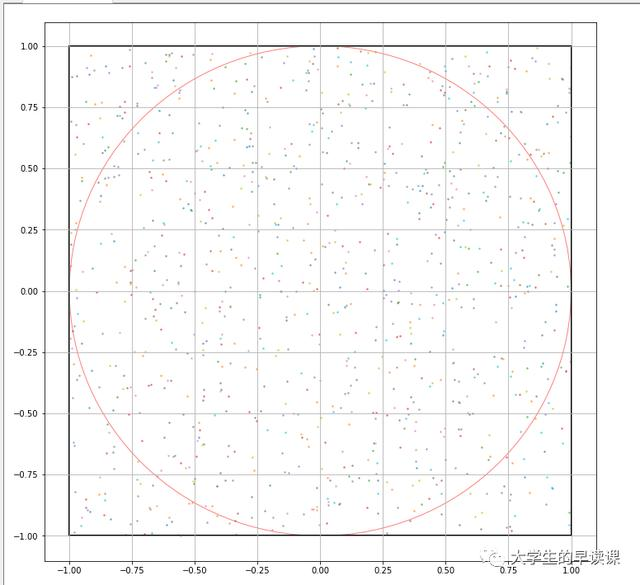
• 假设有若干个随机的点分布在正方形内
• 则正方形内点的个数和内切圆内点的个数之比就近似与正方形和内切圆的面积之比。
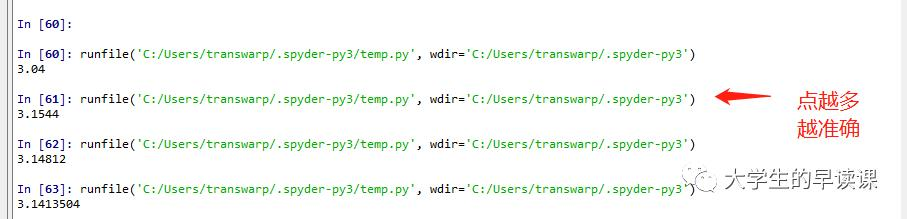
• 点数越多，结果越准确

基本思路

• 通过random产生一系列[-1,1]的随机数坐标(x,y)
• 判断点(x,y)是否落在内切圆内
• 判断的方法是随机点到圆心的距离小于1
• 即满足公式：x^2 + y^2 <= 1

结果

以下分别为枚举点1000，10000，100000，10000000的结果。

代码与效果

import randomimport mathimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom matplotlib.patches import Circlen = 1000#统计在圆内的点数cnt = 0r = 1.0a,b = 0.0,0.0# 设置画布,表示figure 的大小为宽、长（单位为inch）fig = plt.figure(figsize = (12,12))#添加子图ax = fig.add_subplot(1,1,1)while n > 0:    n = n - 1# 从一个均匀分布中随机采样，区间为左闭右开    x = random.uniform(-1,1)    y = random.uniform(-1,1)#画点    plt.scatter(x,y,marker='.',s = 10,alpha = 0.5)#判断点是不是在圆内    if pow(x,2) + pow(y,2) <= 1:        cnt= cnt + 1circle = Circle(xy = (a,b),radius = r, alpha = 0.5 ,fill=False,edgecolor='r')rectangle = plt.Rectangle((-1,-1),2,2,fill=False,edgecolor='black', linewidth=2)ax.add_patch(circle)ax.add_patch(rectangle)plt.grid()pi = 4 * cnt / 1000print("pi=" + str(pi))