关于CLAPACK的使用网上的资料并不多。主要就是官方网站上的安装说明,以 及LAPACK官方论坛上的一些资料。然而,国外一般科研使用的平台都是UNIX或LINUX, 所以对于windows上使用CLAPACK的相关介绍就很少。幸运的是,官方提供了CLAPACK的windows版本,而且还有专门的 VisualStudio工程包。所以,对于广大VS用户来说可谓非常之方便。
然而,即使如此,很多人在使用的过程中还是出现这样那样的问题。其中,多数的情况都是出在编译的时候。而且上网提问多数都没人能够解答。
鉴于此,本人就对如何在VC上编译和使用CLAPACK库,作下简单的说明。
1、什么是CLAPACK:
CLAPACK是LAPACK的C语言接口。LAPACK的全称是Linear Algebra PACKage,是非常著名的线性代数库。原版的LAPACK是用Fortran写的,为了方便C/C++程序的使用,就有了LAPACK的C接口CLAPACK。
LAPACK的主页是 http://www.netlib.org/lapack/
CLAPACK则在 http://www.netlib.org/clapack/。
这两个库都是开源的,可以在官方网站免费下载和使用。
2、CLAPACK的安装:
所谓的安装其实就是把源代码编译成我们可以调用的库.lib文件。
首先从主页上下载CLAPACK包。http://www.netlib.org/clapack/ 上有很多版本。我们选择
http://www.netlib.org/clapack/CLAPACK-3.1.1-VisualStudio.zip
大小: 42MB
版本: 3.1.1
是专门提供给VS用户的。
(注意:VS的版本不能太低。VC6.0是无法使用的。VS2005及以上都应该没问题。本人用的是VS2008。测试的时候发现工程文件版本太老,还需要转换一下呢。当然转换后运行也很正常。如果你坚持要使用VC++6.0那请下载http://www.netlib.org/clapack/CLAPACK3-Windows.zip 这是CLAPACK3.0版,比我介绍的版本3.1.1版要旧一些)
下载解压后,我们可以看到如下目录结构:
\SRC CLAPACK的源代码
\BLAS BLAS的源代码
\F2CLIBS F2C的源代码
\LIB 编译后的库文件.lib
\INCLUDE 头文件
\TESTING 一些使用范例程序
\INSTALL 里面有UNIX和其他平台下安装的文件和方法。lawn81.pdf文件是CLAPACK的使用说明,大家使用的时候可以看看。
这里我要提醒大家。虽然软件包里已经有编译好的.lib文件,就在\LIB中。但是我建议大家不要直接使用他们,还是自己编译一下再用才保险。很多人就是因为直接使用他们而出错的。这点非常重要!如果你就是直接调用他们失败的,那不妨先自己编译一下再试试。
另外,CLAPACK需要F2CLIBS库,并且使用了blas和tmglib这两个外部的库。这几个库都已经包含在了CLAPACK的安装包中。所以,大家无需另外下载。当然,使用前我们还是要重新编译一下的,原因上面已经说过了。
接下来,我详细地讲讲如何编译他们。
首先双击 clapack.vcproj打开工程项目文件。工程中已经包含了所有的子项目。
我们根据个人需要,编译成debug模式,或者release模式。为了能在自己的程序调用中方便的进行debug,我这里就以debug模式为例说明。我的系统是win32。如果你是64位系统也是支持的,操作方法类似。
首先编译F2CLIBS,用于将fortran转换为c语言。
选择libf2c子项目。直接生成之。编译过程中可能会有一些warning,不要理会他们。编译成功后,输出文件是libf2cd.lib。这里的d就 是debug模式,如果是release模式就是libf2cd.lib。输出文件默认路径是\LIB文件夹。注意,\LIB\Win32下已经有一些 lib了。大家最好把他们都先删除了,以免新旧文件混淆。
接着编译tmglib。这是一个矩阵库。
这个库在TESTING\MATGEN里面。选择他生成就好了。
输出文件还是在\LIB里面。文件名是tmglibd.lib。
然后是编译blas,选择项目blas, 编译之。输出文件BLASd.lib。
最后是编译CLAPACK,生成clapackd.lib.
其他模式对应的输出文件大家可以参看下表。
这里需要注意的是,不同模式间不要混合使用。
Win 32
| Configuration | F2c | Reference BLAS | CLAPACK | CBLASWRAP | F77BLASWRAP | TMGLIB |
| Win32 – Release | ||||||
| Win32 – Release no wrap | ||||||
| Win32 – Debug | ||||||
| Win32 – Debug no wrap |
x64
| Configuration | F2c | Reference BLAS | CLAPACK | CBLASWRAP | F77BLASWRAP | TMGLIB |
| x64 – Release | ||||||
| x64 – Release no wrap | ||||||
| x64 – Debug | ||||||
| x64 – Debug no wrap |
3、如何调用CLAPACK:
前面,我们已经生成了CLAPACK的库文件了。那么如何在自己的程序中使用他们呢?
其实很简单。你所需要的只有两部分:
1)头文件
头文件就是.h文件。存放在\INCLUDE中。在自己的工程里加入这个目录就行了。里面的文件最好不要作任何修改。程序中主要调用的头文件是clapack.h和f2c.h。
2)库文件
库文件就是我们前面编译生成的那些lib文件了。
这里,我就以一个具体的调用实例详细地说明如何在VC中设置和使用CLAPACK。
首先,VC中项目的设置方式是:
项目的属性里。C/C++选项卡中,附加包含目录里添加\INCLUDE目录。
连接器选项卡中。附加库目录里添加\LIB\Win32目录。然后附加依赖项添加libf2cd.lib BLASd.lib clapackd.lib tmglibd.lib。(根据不同的编译模式和个人需要以及系统需要选择库文件)
另外,如果想在调试时能对库函数进行源码级调试。那么需要在VS的 工具–选项–项目和解决方案–VC++目录 中添加\SRC的目录。
本文,我们将调用CLAPACK的一个函数dgesvd_()来学习使用的方法。
注意: 包括此函数在内的所有的CLAPACK函数可以在\SRC下找到源代码,并在代码中有函数参数的说明信息。dgesvd_的代码文件就是dgesvd.c。
dgesvd_的函数声明:
int dgesvd_(char *jobu, char *jobvt, integer *m, integer *n,
doublereal *a, integer *lda, doublereal *s, doublereal *u, integer *
ldu, doublereal *vt, integer *ldvt, doublereal *work, integer *lwork,
integer *info)
dgesvd_的功能是对一个实矩阵A进行SVD分解(singular value decomposition)。
即 A = U * SIGMA * transpose(V)
dgesvd.c文件里有详细地函数说明和参数说明。
SIGMA is an M-by-N matrix which is zero except for its
min(m,n) diagonal elements, U is an M-by-M orthogonal matrix, and
V is an N-by-N orthogonal matrix. The diagonal elements of SIGMA
are the singular values of A; they are real and non-negative, and
are returned in descending order. The first min(m,n) columns of
U and V are the left and right singular vectors of A.
Note that the routine returns V**T, not V.
…………………………………..
参数的具体说明也请参看这个文件的 Arguments部分
代码:
#include <stdio.h>
#include <process.h>
//因为程序是C++,而CLAPACK是f2c程序转换的C语言版本,所以在此处用extern关键字调用
extern”C”
{
#include <f2c.h>
#include <clapack.h>
}
#define SIZE 4
int main()
{
char JOBU;
char JOBVT;
int i;
//数据类型integer是fortran里的。这里在C++下可以使用的原因是f2c.h文件中已经作了定义
integer M = SIZE;
integer N = SIZE;
integer LDA = M;
integer LDU = M;
integer LDVT = N;
integer LWORK;
integer INFO;
integer mn = min( M, N );
integer MN = max( M, N );
double a[SIZE*SIZE] = { 16.0, 5.0, 9.0 , 4.0, 2.0, 11.0, 7.0 , 14.0, 3.0, 10.0, 6.0, 15.0, 13.0, 8.0, 12.0, 1.0};
double s[SIZE];
double wk[201];
double uu[SIZE*SIZE];
double vt[SIZE*SIZE];
JOBU = ‘A’;
JOBVT = ‘A’;
LWORK = 201;
/* Subroutine int dgesvd_(char *jobu, char *jobvt, integer *m, integer *n,
doublereal *a, integer *lda, doublereal *s, doublereal *u, integer *
ldu, doublereal *vt, integer *ldvt, doublereal *work, integer *lwork,
integer *info)
*/
dgesvd_( &JOBU, &JOBVT, &M, &N, a, &LDA, s, uu, &LDU, vt, &LDVT, wk, &LWORK, &INFO);
printf(“INFO=%d \n”, INFO );
for ( i= 0; i< SIZE; i++ ) {
printf(“s[ %d ] = %f\n”, i, s[ i ] );
}
system(“pause”);
return 0;
}
运算结果输出:
INFO=0
s[ 0 ] = 34.000000
s[ 1 ] = 17.888544
s[ 2 ] = 4.472136
s[ 3 ] = 0.000000
注意:这个例子中我们使用的库是clapackd.lib。
libf2cd.lib BLASd.lib tmglibd.lib都没有用到。
总之需要什么库就用什么库。关键点是一定要自己编译生成这些.lib文件来使用。不要用现成的,以免出错。
dgeev
int dgeev_(char *jobvl, char *jobvr, integer *n, doublereal * a, integer *lda, doublereal *wr,doublereal *wi, doublereal *vl,
integer *ldvl, doublereal *vr, integer *ldvr, doublereal *work,integer *lwork, integer *info);
首先,最明显的是,所有参数都按照指针传入。
然后这套函数库有个共同的习惯,即要求调用者来处理空间,包括提供返回值的空间,用来计算的临时空间。
函数命名:
d表示double。ge表示general,说明是普通矩阵,按照列主序存储。
ev表示eigenvector吧(疑问语气),表达的是函数的功能。
用到的类型解释:
char*,是字符串类型,但LAPACK的函数只关注该字符串的第一个字符integer,就是C里面的int,一般用来指定维度
doublereal,就是C里面的double,参数类型和函数前缀统一(这里是d)
各个参数:
char *jobvl, 第一个字符为’N’,表示不求左特征向量,为’V’表示要求
char *jobvr, 同上,是对右特征向量的选项
integer *n, 矩阵的列数
doublereal *
a, 存储A矩阵的空间(列主序!!)
integer *lda, A矩阵的行数
doublereal *wr, 返回的特征值,实部
doublereal *wi, 返回的特征值,虚部
doublereal *vl, 左特征向量的存储空间,大小为ldvl*n
integer *ldvl, 左特征向量存储空间的行数
doublereal *vr, 右特征向量的存储空间,大小为ldvr*n
integer *ldvr, 右特征向量存储空间的行数
doublereal *work, 工作空间,一般至少要4*n
integer *lwork, 工作空间的大小
integer *info,返回信息,0表示成功,-i表示第i个参数有问题,+i表示执行错误
具体的看一下代码就明白了,
实在觉得恼火的,照搬着用也行。。
示例代码:
#include < stdio.h>
#pragma comment(lib , “blas.lib”)
#pragma comment(lib , “clapack.lib”)
void *malloc(size_t n) ;
#include “f2c.h”
#include “clapack.h”
int main(void)
{
/* 3×3 matrix A
* 76 25 11
* 27 89 51
* 18 60 32
*/
doublereal A[9] = {76, 27, 18, 25, 89, 60, 11, 51, 32};
integer info ;
int i , j ;
char jobvl = ‘V’ ;
char jobvr = ‘V’ ;
integer n = 3 ;
doublereal *a = A ;
integer lda = 3 ;
doublereal* wr = (doublereal*)malloc( sizeof(doublereal) * n) ;
doublereal* wi = (doublereal*)malloc( sizeof(doublereal) * n) ;
integer ldvr = 3 ;
doublereal* vr = (doublereal*)malloc( sizeof(doublereal) * n * ldvr) ;
integer ldvl = 3 ;
doublereal* vl = (doublereal*)malloc( sizeof(doublereal) * n * ldvl) ;
integer lwork = n * 4 ;
doublereal *work = (doublereal*)malloc( sizeof(doublereal) * lwork) ;
dgeev_(&jobvl, &jobvr, &n, a, &lda, wr, wi, vl , &ldvl , vr, &ldvr, work, &lwork, &info) ;
printf(“info:%d\n” , info) ;
printf(“D = \n”) ;
for ( i = 0 ; i < n ; i ++ ){
for ( j = 0 ; j < n ; j ++ ){
if ( i == j ) printf(“%10.5f” , wr[i]) ;
else printf(“%10.5f” , 0.0) ;
}
printf(“\n”) ;
}
printf(“Vl = \n”) ;
for ( i = 0 ; i < n ; i ++ ){
for ( j = 0 ; j < n ; j ++ ){
printf(“%10.5f” , vl[n * j + i]) ;
}
printf(“\n”) ;
}
printf(“Vr = \n”) ;
for ( i = 0 ; i < n ; i ++ ){
for ( j = 0 ; j < n ; j ++ ){
printf(“%10.5f” , vr[n * j + i]) ;
}
printf(“\n”) ;
}
return info;
}
MATLAB仿真
特征值首先是描述特征的。比如你的图片是有特征的,并且图片是存在某个坐标系的。特征向量就代表这个坐标系,特征值就代表这个特征在这个坐标方向上的贡献。总之,就是代表在对应坐标轴上的特征大小的贡献.
所对应的特征向量,在R中可以用eigen()函数得到U和Λ。例如:
eigen函数参数如下 :
> args(eigen)
function (x, symmetric, only.values = FALSE, EISPACK = FALSE)
NULL其中,x参数输入矩阵;symmetric参数判断矩阵是否为对称矩阵,如果参数为空,系统将自动检测矩阵的对称性。例如:
> A=matrix(1:9,nrow=3,ncol=3)
> A
[,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9eigen(A)得到一个list, 存储特征值和特征向量.
> class(eigen(A))
[1] "list"
> Aeigen=eigen(A)
> Aeigen
$values
[1] 1.611684e+01 -1.116844e+00 -4.054214e-16
$vectors
[,1] [,2] [,3]
[1,] -0.4645473 -0.8829060 0.4082483
[2,] -0.5707955 -0.2395204 -0.8164966
[3,] -0.6770438 0.4038651 0.4082483
得到矩阵A的特征值:
> Aeigen$values
[1] 1.611684e+01 -1.116844e+00 -4.054214e-16得到矩阵A的特征向量:
> Aeigen$vectors
[,1] [,2] [,3]
[1,] -0.4645473 -0.8829060 0.4082483
[2,] -0.5707955 -0.2395204 -0.8164966
[3,] -0.6770438 0.4038651 0.4082483椭圆方程

请问,如果已经知道一个斜椭圆的一般方程a*x^2+b*x*y+c*y^2+d*x+e*y=f,如何用MATLAB来求解它的长半轴、短半轴和旋转角呢?
我仔细地研究过您的“Matlab如何画椭圆(总结帖)”这篇帖子,认为长短半轴可以这样求解:
delta=b^2-4*a*c;
%斜椭圆的几何中心(Xc,Yc)
Xc=(b*e-2*c*d)/delta;
Yc=(b*d-2*a*e)/delta;
r=a*Xc^2+b*Xc*Yc+c*Yc^2+f;
%斜椭圆长短半轴
aa=sqrt(r/a);
bb=sqrt(-4*a*r/delta);
dgemm_
这里以使用dgemm_函数为例,对CLAPACK的使用方法进行说明。从dgemm_的命名可以看出,这是双精度(d)的在一般矩阵(GE)执行matrix-matrix操作的函数,更具体来说,是执行C = alpha* op(A)* op(B) + beta * C操作。在clapack.h中的声明如下:
int dgemm_(char *transa, char *transb, integer *m, integer *n, integer *k, doublereal *alpha, doublereal *a, integer *lda, doublereal *b, integer *ldb, doublereal *beta, doublereal *c__, integer *ldc);
其中
transa表示op(A)的操作,若transa = ‘T’,则表示对A进行转置
transa表示op(B)的操作
m表示矩阵A的行数
n表示矩阵B的列数
k表示矩阵A的列数
alpha就是alpha的值
a就是矩阵A的一维存储,注意调用的函数会认为其是列主序的
lda表示矩阵A的第一维(LDA specifies the first dimension of A),其值根据transa的值而变
b是矩阵B的一维存储
ldb表示矩阵B的第一维,其值根据transb的值而变
c是矩阵C的一维存储
ldc表示矩阵C的第一维。
以下程序将计算
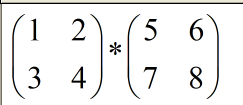
//author: Zero #include "iostream" #include "f2c.h" #include "clapack.h" using namespace std; int main() { char transa = 'T', transb = 'T'; integer M = 2, N = 2, K = 2, LDA = K, LDB = N, LDC = M; double alpha = 1.0, A[4] = { 1, 2, 3, 4}, B[4] = { 5, 6, 7, 8 }, beta = 0.0, C[4]; //下面的函数的意思是C = 1.0 * T(A) * T(B) + 0 * C,其中T()表示将某个矩阵转置 //注意此时得到的C是按列存放的 dgemm_(&transa, &transb, &M, &N, &K, &alpha, A, &LDA, B, &LDB, &beta, C, &LDC); cout<<C[0]<<" "<<C[2]<<endl; cout<<C[1]<<" "<<C[3]<<endl; return 0; }
