如有错误，感谢指正

如有错误，感谢指正，请私信博主，有辛苦红包，拜“一字之师”。

请根据目录寻找自己需要的段落

导语：本博客为个人整理数模算法学习记录帖，如有错误，感谢指正。系统学习，欢迎持续关注，后续陆陆续续更新
Java 交流qq群 383245788

序

本文旨在记录个人数模美赛备赛经历。转载请注明出处。
本文所涉及的感知机模型仅为简单介绍和数模用法，且应用范围较小，比较偏门

感知机模型

感知机Pereptron)是二分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和1。感知机对应于输入空间(特征空间)中将实例划为正负两类的分离超平面，属于判别模型。
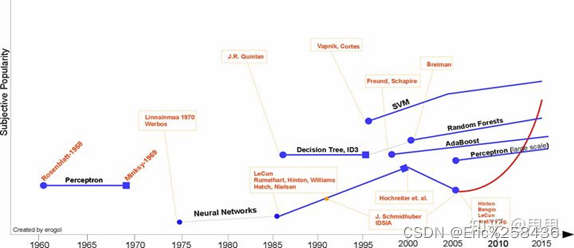
机器学习发展历史

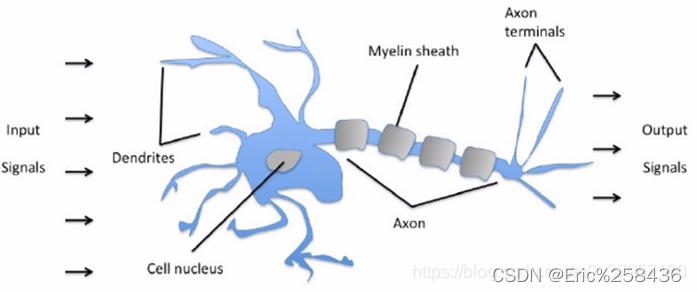
感知机模型生物机制
demo

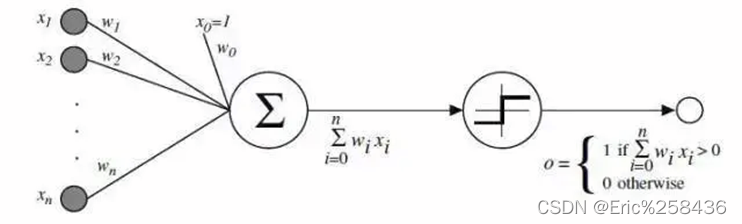
Input:实例的向量，每一列- -个特征
Weight:权重，设置初始值，并使用梯度下降法进行更新
Bias:偏置，允许分类器左右移动决策边界，有助于更好，更快的训练模型。
Weighted sum:加权求和是Input向量和weight的乘积和
Output:输出为类别，取+1，-1
简单说，感知机模型就是数据提取特征后，乘权重，求和利用梯度下降，训练，加偏置辅佐分类，最后二分。

demo

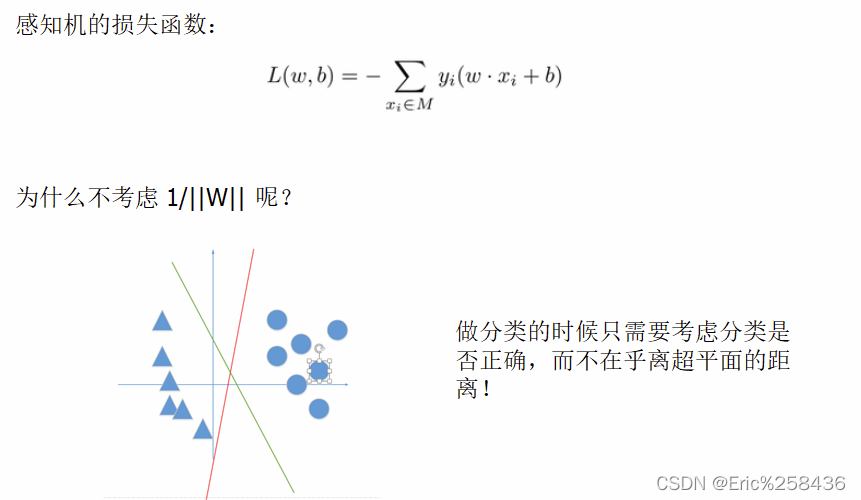
感知机模型的数学模型

给定训练数据集:
T={ (x1,y1) ,(x2,)2)…(x.n,yn) }
其中xi∈Rn, yi ∈{+1-1}，i=1,2,.,.n,
输入x表示实例的特征向量，对应输入空间的点，输出的y代表样本的类别。.
则感知机模型为:
fun
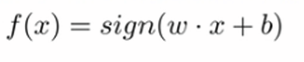
符号函数为：
fun

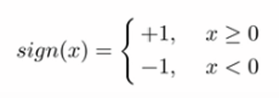
几何解释
demo
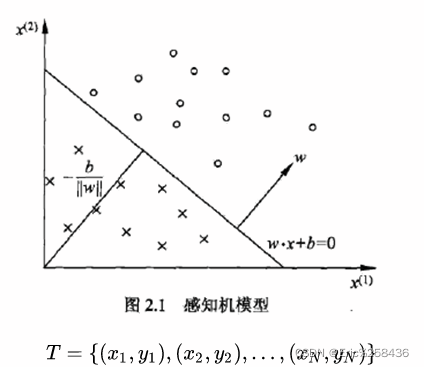
线性方程:wx+b=0
对应超平面S，w为法向量，b截距，分离正负类

仅可以解决二分，如果区别不明显或者交叉，很难求解。典型的错误驱动算法。

demo demo

模型求解

输入:训练数据集T={(x1,y1),(x2,)2)…(xn,yn)}
其中xi∈R, yi∈{-1，+1}， i=12…N
学习率η (0<n<=1) ;
输出: w,b
感知机模型: f(x)=sign(wx+b)
(1)选择初始值w0,b0
(2)在训练集中选取数据(xi,yi)
(3)如果yi(w*xi+b)<=0
(4)求偏导，更新参数
(5)重复(2)直到训练集中没有误分类点

可分

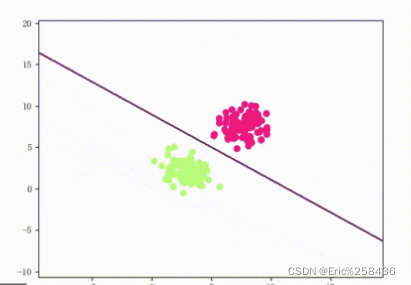
难分
bad

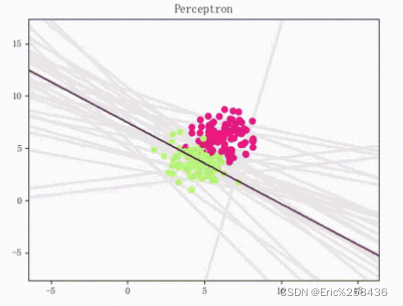
matlab代码

function [W,b] = perceptron(X,y,Maxstep)
%感知机学习算法
%W为待求的权重向量，b为偏差
%X为输入空间,本次取二维的，y为输出空间，取值为[-1,1]
[n,m] = size(X);%求解矩阵X的大小
%给权值和偏差赋初始值，指定学习步长
W = zeros(m, 1);%W为m行的列向量
b=0;%设置偏差的初始值为0
mu= 0.5;%将学习步长设置为0.5，0<mu<=1
for step = 1:Maxstep%迭代更新参数值
	miss_flag=true;%设置一个标志位用来判断是否存在误分类点
	fori=1:n%
		if (i)*(X(;)*W+b))< =0%判断随机选择的点是否是误分类点
			miss_ flag = false;%若随机选择的点是误分类点，则将标志位设置为false
			%根据梯度下降法更新权重和偏差参数
			W = W + mu*y(i)*X(i;); 
			b= b + mu*y(i); .
		end
	end
	if miss_ flag == true%如果标志位为true,表示误分类点数为0，算法已经实现正确分类，不需要继续迭代更新了，跳出循坏
		break
	end
end

clc
%指定输入空间
X = [3,3;4,3;1,1];
%指定输出空间
y=[1,1,-1];
n = size(y,2);%求解y的列长度
%绘制出特征空间中的实例点
forj = 1:n
	if y(j) == 1%绘制正实例点
		plot(X(,1),X(j,2),r*);
	end
	if y(j) == -1%绘制负实例点
		plot(XGj,1),X(j,2),b*);
	end
	hold on %该语句可以在原图的基础上绘制新的图像，不加则只能看到最后一一个点
end
%调用函数更新参数
[W,b] = perceptron(X,y,2000);
xlabel =linspace(0,5,500);
ylabel = -(W(1)/W(2))*xlabel -b/W(2);%将X(2)看成因变量，X (1)看作自变量，故可以得出算法绘制出的超平面
plot(xlabel,ylabel);

原文链接：https://blog.csdn.net/m0_52074396/article/details/122929699

** 如有错误，感谢指正**