博客

数据分析课设（SPSS,EVIEWS,R）【理论】

  • Post author:
  • Post category:其他


对外汇数据作前向、后向以及逐步回归，并对输出结果作分析和理论解释。


x1
x2
x3
x4
x5
x6
x7
x8
x9
x10
x11
x12
省市
y

1.94
4.5
154.45
207.33
246.87
277.64
135.79
30.58
110.67
80.83
51.83
14.09
北 京
2384

0.33
6.49
133.16
127.29
120.17
114.88
81.21
14.05
35.7
16
27.1
2.93
天 津
202

6.16
17.18
313.4
386.96
202.98
204.22
79.43
32.42
79.38
14.54
128.13
42.15
河 北
100

5.35
9.3
123.8
122.94
101.59
96.84
34.67
13.99
37.28
5.93
63.91
3.12
山 西
38

3.78
4.26
106.05
95.49
27.58
22.75
34.24
14.06
28.2
4.69
35.72
9.51
内蒙古
126

11.17
8.17
271.96
533.15
164.4
123.78
187.7
58.63
90.52
31.71
84.05
11.61
辽 宁
262

2.84
3.61
109.37
130.8
52.49
62.26
38.15
21.82
44.53
25.78
48.49
14.22
吉 林
38

8.64
11.41
160.06
246.57
109.18
115.32
68.71
34.55
58.08
13.52
72.05
21.17
黑龙江
121

3.64
6.67
244.42
412.04
459.63
512.21
160.45
43.51
89.93
48.55
48.63
7.05
上 海
1218

30.89
19.08
435.77
724.85
376.04
381.81
210.39
71.82
150.64
23.74
188.28
19.65
江 苏
529

6.26
6.3
321.75
665.8
157.94
172.19
147.16
52.44
78.16
10.9
93.05
9.45
浙 江
361

4.13
8.87
152.29
258.6
83.42
85.1
75.74
26.75
63.47
5.89
47.02
2.66
安 徽
51

5.85
5.61
347.25
332.59
157.32
172.48
115.16
33.8
77.27
8.69
79.01
8.24
福 建
651

6.7
6.8
145.4
143.54
97.4
100.5
43.28
17.71
51.03
5.41
62.03
18.25
江 西
43

10.8
11.73
442.2
665.33
411.89
429.88
115.07
87.45
145.25
21.39
187.77
110.2
山 东
220

4.16
22.51
299.63
316.81
132.57
139.76
84.79
53.93
84.23
12.36
116.89
10.38
河 南
101

4.64
7.65
195.56
373.04
161.84
180.14
101.58
58
80.53
21.61
100.69
5.16
湖 北
88

7.08
10.99
216.49
291.73
119.22
125.62
47.05
48.19
97.97
12.07
139.39
16.67
湖 南
156

16.3
24.1
688.83
827.16
271.07
268.2
331.55
71.44
146.15
23.38
145.77
16.52
广 东
2942

4.01
4
125.04
243.5
52.06
31.22
47.25
25.59
55.27
4.49
60.13
13.64
广 西
156

0.8
2.07
35.03
60.9
29.2
30.14
20.22
4.22
12.19
1.3
9.29
0.27
海 南
96

4.42
2.11
78.93
138.43
68.31
73.84
79.98
18.42
43.3
20.01
48.48
0.72
重 庆
88

11.18
9.42
196.27
328.46
204.49
144.45
101.21
43.01
74.22
15.85
90.6
11.05
四 川
84

2.01
2.03
25.04
69.97
40.86
36.45
27.02
13.8
26.83
2.86
25.63
6.76
贵 州
48

6.43
6.08
88.9
170.15
88.86
89.84
33.66
29.2
51.25
8.6
40.47
4.81
云 南
261

1.91
0.98
5.08
11.13
0.67
1.69
1.94
2.95
5.02
0.89
7.59
0.17
西 藏
33

5.49
9.9
115.42
94.63
76.57
53.14
47.88
22.08
56.97
14.02
48.64
38.17
陕 西
247

3.97
7.8
39.32
99.23
41.64
50.55
11.41
8.81
15.98
6.33
16.46
7.02
甘 肃
30

1.31
3.08
13.67
18.79
18.37
18.57
3.15
3.14
8.66
1.26
14.3
1.2
青 海
3

1.1
2.1
16.11
19.64
17.85
16.52
4.16
3.03
6.76
1.06
7.52
3.18
宁 夏
1

4.58
10.35
92.03
103.34
49.19
50.2
28.14
11.82
37.95
4.52
39.49
3.53
新 疆
82

向前向后略，仅展示逐步



模型摘要


模型


R


R


方


调整后 R 方


标准估算的错误


更改统计


R


方变化量


F


变化量


显著性 F 变化量


AIC


（


Eviews


结果


）


1


.741a


.549


.533


455.9279


.549


35.261


.000


15.14489


2


.835b


.697


.675


380.4405


.148


13.650


.001


14.81230


3


.860c


.739


.710


359.3347


.042


4.386


.046


14.72630


4


.885d


.783


.749


334.0439


.044


5.243


.030


14.60711


5


.908e


.824


.789


306.8386


.041


5.815


.024


14.46251


6


.901f


.812


.783


310.9102


-.012


1.695


.205


14.46358


7


.889g


.791


.768


321.5075


-.021


2.872


.102


14.50383


a.


预测变量：(常量), x7


b.


预测变量：(常量), x7, x4


c.


预测变量：(常量), x7, x4, x10


d.


预测变量：(常量), x7, x4, x10, x3


e.


预测变量：(常量), x7, x4, x10, x3, x11


f.


预测变量：(常量), x4, x10, x3, x11


g.


预测变量：(常量), x10, x3, x11



系数a


模型


未标准化系数


标准化系数


t


显著性


B


标准错误


Beta


1


(


常量)


-209.535


124.469


-1.683


.103


x7


6.907


1.163


.741


5.938


.000


2


(


常量)


-96.142


108.300


-.888


.382


x7


13.791


2.101


1.479


6.564


.000


x4


-2.520


.682


-.832


-3.695


.001


3


(


常量)


-174.886


108.984


-1.605


.120


x7


11.152


2.351


1.196


4.744


.000


x4


-2.034


.685


-.672


-2.970


.006


x10


10.761


5.139


.260


2.094


.046


4


(


常量)


-228.815


104.015


-2.200


.037


x7


8.786


2.417


.942


3.635


.001


x4


-3.261


.832


-1.077


-3.919


.001


x10


13.864


4.965


.335


2.792


.010


x3


2.849


1.244


.647


2.290


.030


5


(


常量)


-140.625


102.304


-1.375


.181


x7


3.910


3.003


.419


1.302


.205


x4


-1.997


.927


-.660


-2.154


.041


x10


18.431


4.939


.446


3.732


.001


x3


5.090


1.473


1.157


3.455


.002


x11


-7.442


3.086


-.551


-2.411


.024


6


(


常量)


-127.159


103.130


-1.233


.229


x4


-1.289


.761


-.426


-1.695


.102


x10


22.650


3.776


.548


5.998


.000


x3


6.375


1.108


1.448


5.753


.000


x11


-10.148


2.312


-.751


-4.389


.000


7


(


常量)


-117.497


106.482


-1.103


.280


x10


21.479


3.839


.519


5.595


.000


x3


4.975


.764


1.130


6.516


.000


x11


-11.264


2.292


-.834


-4.916


.000


a.


因变量：y

分析：

最终得到     y=-117.497+21.479×10+4.975×3-11.264×11

对比

前向法：y=-140.625+3.910×7-1.997×4+18.431×10+5.090×3-7.442×11

后向法：y=-184.69+4.325×3-20.188×8+17.334×9+11.644×10-12.998×11

可以发现x3 x10 x11最后均在三种方法中保存下来，再一次验证了这三个变量更适合进行回归。

根据上述统计量R^2、R^2调整、AIC：

我们发现前五步和前向法一样，R^2继承了变量增多就增大的传统，一如既往地在变量最多的第五步是数值最大的，而R^2调整不落后尘因为在之前前向法的分析中就是第五步的情况最好，即使后来删减了变量，依然无法撼动x3 x4 x7 x10 x11这一组合的地位！但是真的那么顺利吗？从其他角度（AIC统计量）来看，果真如此，AIC最低值落在了第五步。因此我们有理由确定第五步的情况非常适合拟合回归。

在Eviews下 示例（仅最后一步验证）：


Dependent Variable: Y


Method: Stepwise Regression


Date: 10/26/20   Time: 20:36


Sample: 1 31


Included observations: 31


Number of always included regressors: 1


Number of search regressors: 12


Selection method: Stepwise forwards


Stopping criterion: p-value forwards/backwards = 0.05/0.051


Variable


Coefficient


Std. Error


t-Statistic


Prob.*


C


-117.4965


106.4821


-1.103439


0.2796


X11


-11.26444


2.291584


-4.915569


0.0000


X3


4.975142


0.763533


6.515946


0.0000


X10


21.47859


3.838694


5.595287


0.0000


R-squared


0.791069


Mean dependent var


347.0968


Adjusted R-squared


0.767854


S.D. dependent var


667.2840


S.E. of regression


321.5075


Akaike info criterion


14.50383


Sum squared resid


2790910.


Schwarz criterion


14.68886


Log likelihood


-220.8094


Hannan-Quinn criter.


14.56415


F-statistic


34.07639


Durbin-Watson stat


1.242992


Prob(F-statistic)


0.000000


Selection Summary


Added X7


Added X4


Added X10


Added X3


Added X11


Removed X7


Removed X4


*Note: p-values and subsequent tests do not account for stepwise


selection.

对数据进行岭回归，lasso，pca分析


R-SQUARE AND BETA COEFFICIENTS FOR ESTIMATED VALUES OF K


K     RSQ      x1       x2       x3       x4       x5       x6       x7       x8       x9      x10      x11      x12


______ ______ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________


.00000 .87481 -.012491  .022873  .749084 -.312414 -.962825  .759538  .446284 -.519848 1.037980  .221303 -.780227  .041865


.01000 .86789 -.055610  .027677  .719018 -.255572 -.437414  .293662  .441002 -.505298  .786637  .287679 -.611372  .013926


.02000 .85976 -.072465  .038023  .657698 -.220189 -.298092  .180214  .464919 -.476889  .638421  .315486 -.513426  .006697


.03000 .85231 -.081208  .046847  .608603 -.190878 -.229206  .128640  .475058 -.448808  .541643  .331856 -.452919  .000636


.04000 .84548 -.086395  .053850  .568792 -.166619 -.186798  .099777  .477484 -.422877  .473334  .342069 -.411422 -.005267


.05000 .83915 -.089680  .059310  .535619 -.146433 -.157441  .081835  .475775 -.399303  .422456  .348511 -.380745 -.011018


.06000 .83322 -.091812  .063540  .507358 -.129465 -.135565  .069969  .471786 -.377934  .383053  .352488 -.356796 -.016545


.07000 .82761 -.093180  .066799  .482864 -.115043 -.118424  .061811  .466521 -.358540  .351621  .354782 -.337326 -.021796


.08000 .82227 -.094013  .069294  .461342 -.102654 -.104497  .056063  .460552 -.340887  .325957  .355890 -.321000 -.026744


.09000 .81717 -.094454  .071183  .442221 -.091906 -.092868  .051953  .454219 -.324766  .304602  .356142 -.306981 -.031380


.10000 .81228 -.094598  .072588  .425075 -.082500 -.082952  .048998  .447729 -.309990  .286554  .355766 -.294715 -.035706


.11000 .80757 -.094512  .073606  .409582 -.074202 -.074354  .046876  .441214 -.296399  .271099  .354920 -.283822 -.039732


.11000 .80757 -.094512  .073606  .409582 -.074202 -.074354  .046876  .441214 -.296399  .271099  .354920 -.283822 -.039732


.12000 .80302 -.094244  .074312  .395489 -.066831 -.066798  .045369  .434753 -.283859  .257715  .353722 -.274031 -.043472


.13000 .79863 -.093833  .074764  .382596 -.060240 -.060082  .044324  .428399 -.272249  .246011  .352257 -.265143 -.046940


.14000 .79437 -.093306  .075011  .370741 -.054314 -.054059  .043628  .422183 -.261471  .235687  .350589 -.257008 -.050154


.15000 .79025 -.092686  .075089  .359792 -.048958 -.048614  .043200  .416124 -.251435  .226513  .348766 -.249512 -.053129


.16000 .78624 -.091990  .075031  .349641 -.044095 -.043659  .042979  .410232 -.242068  .218305  .346827 -.242563 -.055882


.17000 .78234 -.091232  .074860  .340195 -.039661 -.039124  .042919  .404512 -.233303  .210918  .344801 -.236090 -.058428


.18000 .77854 -.090425  .074597  .331377 -.035601 -.034953  .042984  .398965 -.225084  .204232  .342710 -.230034 -.060781


.19000 .77484 -.089578  .074260  .323122 -.031872 -.031099  .043147  .393589 -.217359  .198151  .340572 -.224347 -.062955


.20000 .77124 -.088699  .073861  .315373 -.028435 -.027525  .043384  .388380 -.210085  .192596  .338403 -.218989 -.064963


.21000 .76772 -.087796  .073413  .308082 -.025258 -.024200  .043680  .383334 -.203223  .187501  .336212 -.213926 -.066816


.22000 .76428 -.086873  .072925  .301206 -.022313 -.021095  .044021  .378446 -.196738  .182808  .334011 -.209128 -.068526


.23000 .76091 -.085935  .072404  .294709 -.019576 -.018190  .044396  .373709 -.190599  .178473  .331805 -.204572 -.070102


.24000 .75762 -.084987  .071859  .288557 -.017027 -.015463  .044796  .369118 -.184779  .174454  .329601 -.200236 -.071555


.25000 .75441 -.084032  .071294  .282722 -.014646 -.012899  .045214  .364668 -.179254  .170717  .327404 -.196101 -.072892


.26000 .75125 -.083073  .070713  .277179 -.012419 -.010483  .045645  .360352 -.174000  .167232  .325218 -.192152 -.074122


.27000 .74816 -.082112  .070122  .271905 -.010331 -.008202  .046083  .356165 -.168998  .163975  .323046 -.188372 -.075253


.28000 .74513 -.081151  .069524  .266879 -.008371 -.006044  .046525  .352102 -.164230  .160922  .320890 -.184751 -.076290


.29000 .74216 -.080193  .068920  .262083 -.006527 -.004001  .046969  .348156 -.159680  .158056  .318752 -.181276 -.077241


.30000 .73925 -.079238  .068314  .257502 -.004789 -.002062  .047411  .344323 -.155332  .155357  .316635 -.177938 -.078111


因为不知道


X1~X12


实际背景下各变量的意义，所以应该根据实际情况（各变量与因变量在实际生活或专业知识中是否是正相关或负相关）以及


K-RSQ


图，


k


（即


lambda


）由小到大来选择，


k


在


0.1~0.2


时，回归系数开始趋于稳定。比如当


K


取


0.2


是，得到的方程为：


y = -0.088699×1 +0.073861×2 +0.315373×3 -0.028435×4 -0.027525×5 +0.043384×6 +0.388380×7 -0.210085×8 +0.192596×9 +0.338403×10 -0.218989×11 -0.064963×12

通过下图对比，可以进一步验证，k=0.2时，各变量的岭迹趋于平稳，再回看上图，k=0.2之后也没有明显的波动，所以两者结论一致。在k=0.2时，虽然RSQ不如k=0时高，但是我们通过减少部分信息换来更好的估计效果，这是值得的。

LASSO

通过Eviews进行Lasso回归，因为Eviews没有直接给LASSO的方法，所以我们可以通过弹性网进行计算，

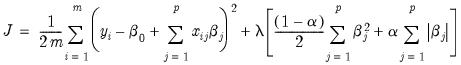
只需要α=1时，可以演变成LASSO方法。

得到以下数据：


Dependent Variable: Y


Method: Elastic Net Regularization


Date: 11/10/20   Time: 20:06


Sample: 1 31


Included observations: 31


Penalty type: LASSO (alpha = 1)


Lambda at minimum error: 92.69


Regressor transformation: Std Dev (smpl)


Cross-validation method: K-Fold (number of folds = 5), rng=kn,


seed=99713398


Selection measure: Mean Squared Error


(minimum)


(+ 1 SE)


(+ 2 SE)


Lambda


92.69


465.3


465.3


Variable


Coefficients


X1


2.10E-08


0.000000


0.000000


X10


10.62391


0.329137


0.329137


X11


0.000000


0.000000


0.000000


X12


-0.331988


0.000000


0.000000


X2


0.000000


0.000000


0.000000


X3


0.392510


0.008381


0.008381


X4


0.000000


0.003180


0.003180


X5


2.21E-09


0.000000


0.000000


X6


0.035251


0.000000


0.000000


X7


2.285083


0.046742


0.046742


X8


4.62E-09


0.000000


0.000000


X9


0.900589


0.203648


0.203648


C


-126.1446


323.2102


323.2102


d.f.


9


5


5


L1 Norm


140.7139


323.8013


323.8013


R-squared


0.573399


0.034777


0.034777

该数据表面最佳lambda取92.69

（

Eviews中对lambda的解释是




Ratio of minimum to maximum lambda for EViews-supplied list




，实际上它只能在0~1之间，这里我对min/max lambda=




0.0001



）

，然而此时x11 x2 x4被去除，而x1 x5 x8的系数对回归方程的影响也微乎其微，我们可以联想到曾经做前进、后退和逐步回归。

因为lasso回归是使用收缩的线性回归，对于最后一项L1范数，事实上约束了模型参数，使得某些变量回归系数缩小为零，也就是之前提到的“收缩”。

经过处理高相关性变量后只留下了9个变量。

通过上图我们可以看出x10在lambda=92之后依然有较大的起伏，但是其他变量都逐渐趋于平稳。

也进一步证明了对于lambda既要取得小又要取得好的92是可行的。

得到以下统计量


Forecast: YF


Actual: Y


Forecast sample: 1 31


Included observations: 31


Root Mean Squared Error


428.7473


Mean Absolute Error


267.1796


Mean Absolute Percentage Error


570.8096


Theil Inequality Coef.


0.344282


Bias Proportion


0.000000


Variance Proportion


0.465991


Covariance Proportion


0.534009


Theil U2 Coefficient


0.520825


Symmetric MAPE


102.9197

我们可以对比普通最小二乘时的结果：


Forecast: YF


Actual: Y


Forecast sample: 1 31


Included observations: 31


Root Mean Squared Error


232.2607


Mean Absolute Error


197.1669


Mean Absolute Percentage Error


1009.038


Theil Inequality Coef.


0.160419


Bias Proportion


0.000000


Variance Proportion


0.033425


Covariance Proportion


0.966575


Theil U2 Coefficient


1.324975


Symmetric MAPE


113.5775


可以发现在添加LASSO正则项后，MSE、平均绝对误差和平均绝对百分误差都上升了。

PCA

通过SPSS可以得到以下特征值贡献率情况：


成分


初始特征值a


总计


方差百分比


累积 %


原始


1


96887.647


87.246


87.246


2


9689.193


8.725


95.971


3


2103.445


1.894


97.865


4


1479.046


1.332


99.197


5


446.118


.402


99.598


6


184.926


.167


99.765


7


143.417


.129


99.894


8


43.857


.039


99.933


9


31.613


.028


99.962


10


27.888


.025


99.987


11


9.475


.009


99.996


12


4.896


.004


100.000


从上表可知

，特征值前两个对总数据表达的贡献程度较高（第一个甚至独占了87.246%的比重，而第二个虽然对比重体来说也比较高（8.725%））然而相比较第一特征值，还是逊色许多。如果从尽可能地包含原信息的角度来说，也可以将第三和第四个特征纳入我们的考虑范围内，但是一般来说，既然都做PCA降维了，没必要还留那么多信息，重点还是希望减少信息得到他们共有的表达变量，从而以少量的变量进行新的表示。

以上碎石图也很直观的能看出前两个特征值对总体表达的占比。


原始


成分


1


2


x1


4.195


-.852


x2


3.970


-1.257


x3


144.276


-29.159


x4


215.711


-36.110


x5


101.999


55.366


x6


105.668


65.480


x7


64.468


-7.777


x8


20.878


-1.153


x9


37.351


2.572


x10


7.254


8.335


x11


42.440


-5.373


x12


9.850


3.595


因此

，SPSS也自动地取了前两个特征，其中由第二列（第一特征值）可以看出它由x3 x4 x5 x6较高程度地影响着，并且是正相关；第三列（第二特征值）其中由x3 x4 x5 x6较高程度地影响着，但是因为这两个特征值所代表的现实意义不同，所以这次只是巧合也是这几个变量影响较大，而且他们也没有第一特征值的时候影响得大，x3 x4和其他几个变量甚至在第二特征值的情况下产生了负相关影响。所以第一第二特征值的实际意义还依赖于现实常识和专业知识的理解。

最后回到协方差矩阵分析：



相关性矩阵


x1


x2


x3


x4


x5


x6


x7


x8


x9


x10


x11


x12


相关性


x1


1.000


.640


.691


.738


.582


.519


.663


.691


.719


.150


.758


.301


x2


.640


1.000


.773


.658


.502


.464


.602


.660


.686


.118


.760


.337



x3



.691



.773



1.000




.934



.742



.710



.885



.867



.889



.314



.855



.457



x4



.738



.658




.934



1.000



.780



.743



.887



.926



.892



.348



.849



.437



x5



.582



.502



.742



.780



1.000



.





989



.740



.790



.850



.630



.705



.515



x6



.519



.464



.710



.743



.





989



1.000



.703



.753



.821



.646



.666



.493


x7


.663


.602


.885


.887


.740


.703


1.000


.781


.834


.541


.649


.190


x8


.691


.660


.867


.926


.790


.753


.781


1.000


.931


.404


.906


.548


x9


.719


.686


.889


.892


.850


.821


.834


.931


1.000


.569


.895


.533


x10


.150


.118


.314


.348


.630


.646


.541


.404


.569


1.000


.241


.155


x11


.758


.760


.855


.849


.705


.666


.649


.906


.895


.241


1.000


.613


x12


.301


.337


.457


.437


.515


.493


.190


.548


.533


.155


.613


1.000


我们发现之前所说的

x3 x4 以及x5 x6两两之间高度相关，我们有理由怀疑，他们两者在多重共线性去重后，再次进行PCA，各变量对第一特征值和第二特征值的影响有可能还是和目前情况差不多。


在岭回归中，dj的缩减对PCA造成何种影响？

对于带有L2正则项的OLS，有以下损失函数：

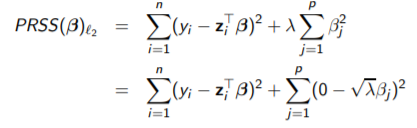
易解：

现在我们需要做SVD分解：

使得

其中U为n*p维正交矩阵，D为p*p维主对角线矩阵，V为p*p维转置正交矩阵

得到：


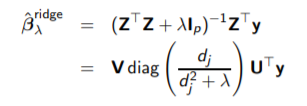
其中dj为D中对角线上的元素。

通过上式括号内的第一项改写：

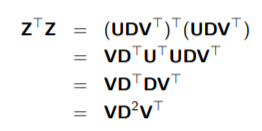
因此可以得到：

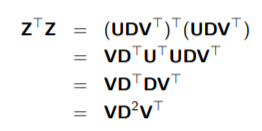
由主成分分析法的公式联想到：设γj为Z矩阵第j个主成分，于是得到以下关系：

γj = Z vj = uj dj

我们发现，

1.uj作为新的变量并向每个

进行投影。

2.

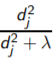
使用它缩减投影。特征值dj较小的方向会产生更大的相对收缩，而变量的大小决定了dj的大小，因此会影响收缩率。当lambda=0时，这一项等于1，而解将退化成最小二乘解，当lambda充分大时，这一项趋于0，

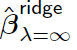
等于0


版权声明：本文为qq_54394719原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。