1、基本概念
a、路径和路径长度
若在一棵树中存在着一个结点序列 k1,k2,……,kj, 使得
k
i
是
k
i+1
的双亲(1<=i<j),则称此结点序列是从 k1 到 kj 的路径。
从 k1 到 kj 所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1.
b、结点的权和带权路径长度
在许多应用中,常常将树中的结点赋予一个有着某种意义的实数,我们称此实数为该结点的权,(如下面一个树中的蓝色数字表示结点的权)
结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积。
c、树的带权路径长度
树的带权路径长度定义为树中所有叶子结点的带权路径长度之和,公式为:
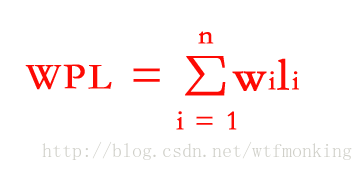
其中,n表示叶子结点的数目,wi 和 li 分别表示叶子结点 ki 的权值和树根结点到 ki 之间的路径长度。
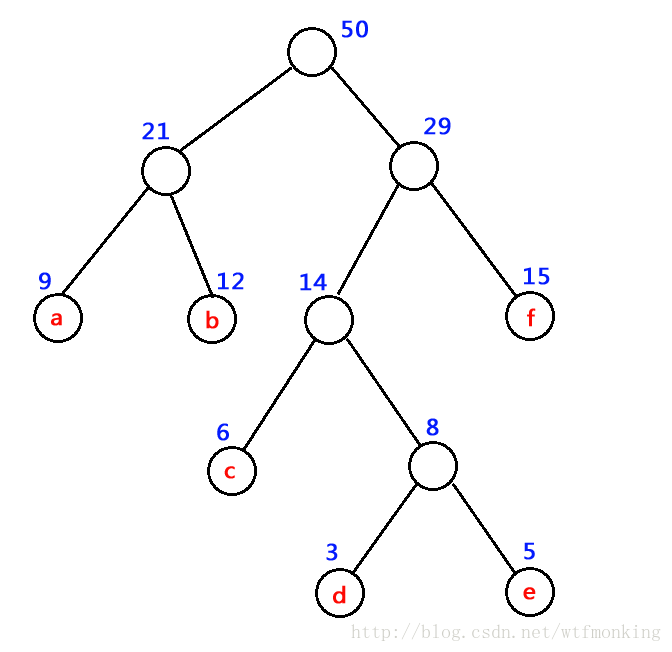
如下图中树的带权路径长度 WPL = 9 x 2 + 12 x 2 + 15 x 2 + 6 x 3 + 3 x 4 + 5 x 4 = 122
d、哈夫曼树
哈夫曼树又称最优二叉树。它是 n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
如下图为一哈夫曼树示意图。
2、构造哈夫曼树
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
如:对 下图中的六个带