本文主要是在阅读过程中对本书的一些概念摘录,包括一些个人的理解,主要是思想理解不涉及到复杂的公式推导。会不定期更新,若有不准确的地方,欢迎留言指正交流
本文完整代码 github 地址:
https://github.com/anlongstory/awsome-ML-DL-leaning/lihang-reading_notes
第六章 逻辑斯特回归与最大熵模型
逻辑斯特回归(logistic regression)是统计学习中的经典分类方法。最大熵是概率模型学习的一个准则,将其推广到分类问题得到最大熵模型。
逻辑斯特回归模型与最大熵模型都属于 对数线性模型
逻辑斯特回归模型
首先明确逻辑斯特分布函数的曲线,在中心附近增长速度较快,在两端增长速度较慢。其形状参数 γ 越小,曲线在中心附近增长越快。
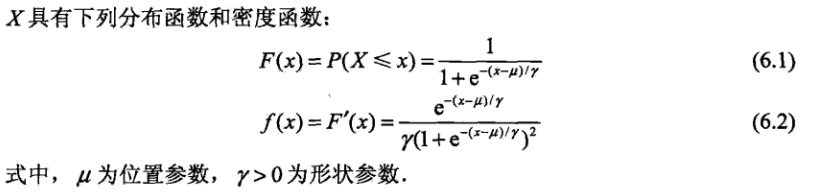
二项逻辑斯特回归模型是一种分类模型,由条件概率 P(Y|X) 表示,形式为参数化的逻辑斯特分布:
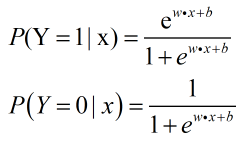
其中 w 为权值向量,b 为偏置。 上述就是概率回归模型。
这里给出几率(odd)的概念,不同于概率,
几率(odd)是指一件事情发生的概率与该事件不发生的概率的比值
如果一件事情发生的概率为 p ,则该事件的对数几率就是:
对于逻辑斯特回归而言,上述对数公式就是:
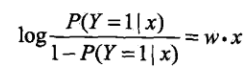
由上面公式可以得到,输出 Y = 1 的对数几率是由输入x 的线性函数表示的模型。
模型参数估计
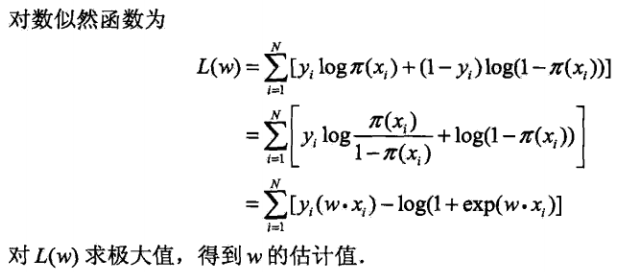
由上问题就变成对数似然函数为目标函数的优化问题,逻辑斯特回归学习中通常使用
梯度下降法
及
拟牛顿法
。
上面的二项逻辑斯特回归可以同等的推广到多项逻辑斯特回归。
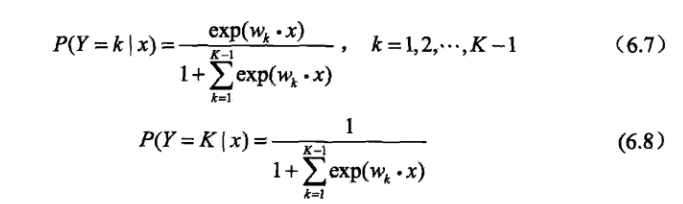
最大熵模型
最大熵原理:在学习概率模型时,在所有可能的概率模型分布中,熵最大的模型就是最好的模型
所以用最大熵原理作为约束条件选取的模型就是最大熵模型。最大熵原理通过熵的最大化来表示等可能性。
所以在模型学习的约束条件就是,特征函数对于联合分布P(X,Y)的经验分布P
’
(X,Y)的期望与特征函数关于模型 P(Y|X)与经验分布P
’
(X)的期望值相等。
满足上诉约束条件的模型集合 C 中求条件熵 H§最大的模型。(关于条件熵的定义及定义式见:
5.决策树
)
最大熵模型学习
因为有条件熵的定义式H(P),有约束条件,所以这里引入拉格朗日乘子 w,定义一个拉格朗日函数 L(P,w),这里 L(P,w)是关于 P 的凸函数,然后对拉格朗日函数进行求解,先求解拉格朗日的最小化,然后得到关于 w 的表达式,再对这个表达式求最大化,得到 w 代入最终的结果。
第二步对 w 的求解过程中,是对偶函数的极大化,其就等同于最大熵模型的极大似然估计。
模型的最优化方法
逻辑斯特回归模型和最大熵模型都是对数线性模型,模型学习就是再给定的训练数据条件下对模型进行极大似然估计或正则化的极大似然估计。
而模型的最优化算法常用的有
改进的迭代尺度法
、
梯度下降法
、
牛顿或拟牛顿法
。
代码运行
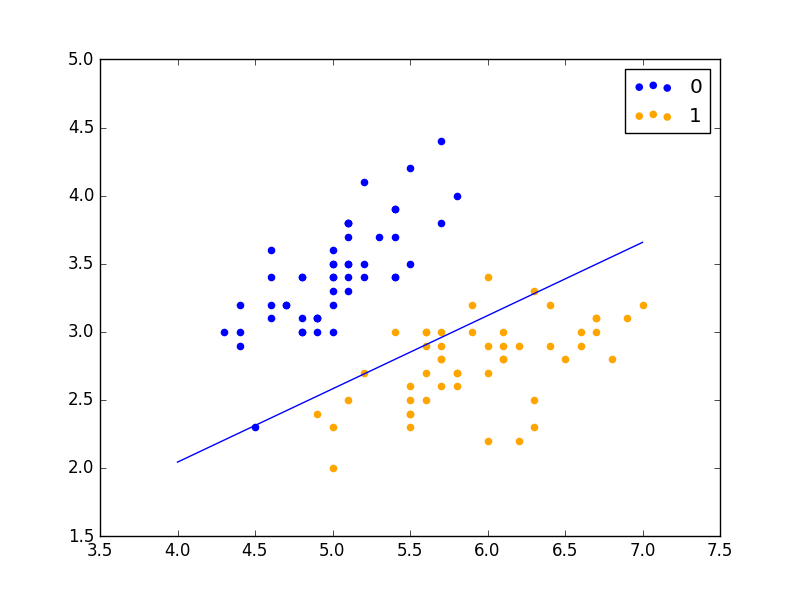
在 iris 数据集上运行
LR.py
结果,可以看到:
学习率为 0.01,迭代 10 次:
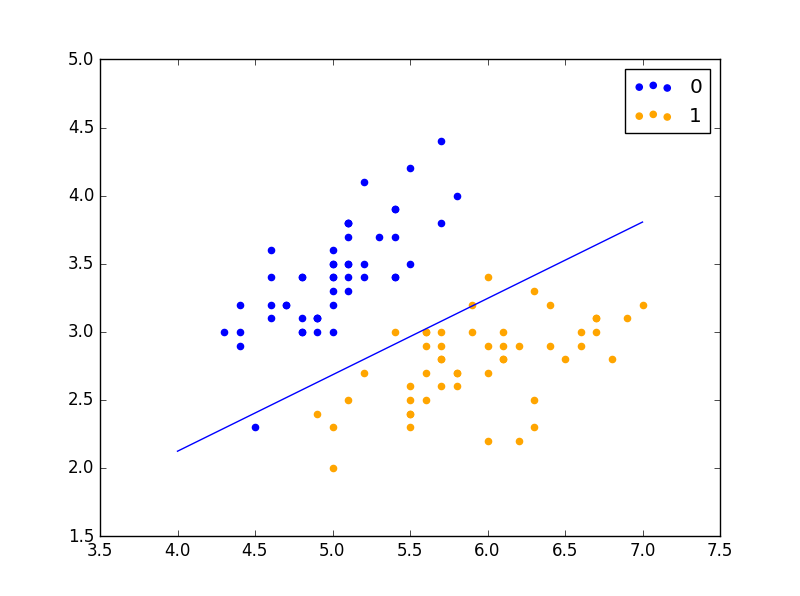
学习率为 0.01,迭代 30 次:
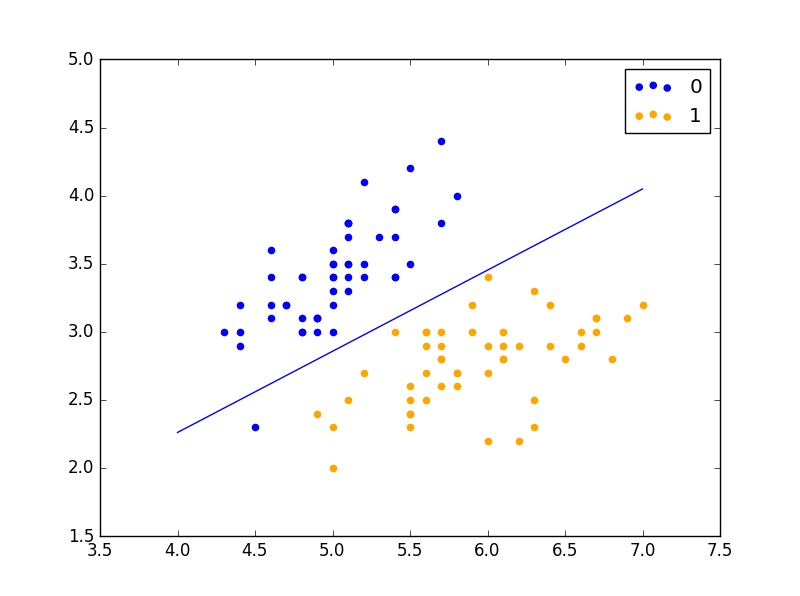
学习率为 0.01,迭代 60 次:
相关阅读:
《统计学习方法》—— 1. 统计学习方法概论(Python实现)
《统计学习方法》—— 2. 感知器(Python实现)
《统计学习方法》—— 3. K近邻法(Python实现)
《统计学习方法》—— 4. 朴素贝叶斯(Python实现)
《统计学习方法》—— 5. 决策树(Python实现)
《统计学习方法》—— 7. 支持向量机(Python实现)
《统计学习方法》—— 8. 提升方法 (Python实现)
《统计学习方法》—— 9. EM 算法(Python实现)
《统计学习方法》——10. 隐马尔可夫模型(Python实现)
《统计学习方法》—— 11. 条件随机场