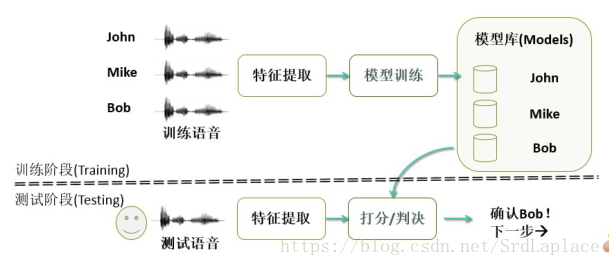
声纹识别定义
声纹识别是通过对一种或多种语音信号的特征分析来达到对未知声音辨别的目的。声纹识别的理论基础是每一个声音都具有独特的特征,通过该特征能将不同人的声音进行有效的区分。
这种独特的特征主要由两个因素决定
- 第一个是声腔的尺寸,具体包括咽喉、鼻腔和口腔等,这些器官的形状、尺寸和位置决定了声带张力的大小和声音频率的范围。因此不同的人虽然说同样的话,但是声音的频率分布是不同的,听起来有的低沉有的洪亮。每个人的发声腔都是不同的,就像指纹一样,每个人的声音也就有独特的特征。
- 第二个决定声音特征的因素是发声器官被操纵的方式,发声器官包括唇、齿、舌、软腭及腭肌肉等,他们之间相互作用就会产生清晰的语音。而他们之间的协作方式是人通过后天与周围人的交流中随机学习到的。人在学习说话的过程中,通过模拟周围不同人的说话方式,就会逐渐形成自己的声纹特征。
因此,理论上来说,声纹就像指纹一样,很少会有两个人具有相同的声纹特征。
语音具备了一个良好的性质,称为短时平稳,在一个20-50毫秒的范围内,语音近似可以看作是良好的周期信号,因此一般处理语音都是用20-50ms分帧处理。
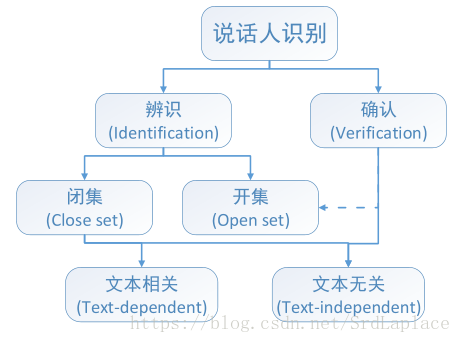
声纹识别分类
文本无关识别,文本相关识别;说话人辨认,说话人确认;开集,闭集等。
预处理
VAD,去噪,解混响,speaker separation等。
声纹识别的评价指标
1.等错误概率EER:当FA和FR相等时的错误概率
2.最小检测代价:
C = C F A P F A ( 1 − P P ) + C F R P F R ( 1 − P N ) C=C_{FA}P_{FA}(1-P_{P})+C_{FR}P_{FR}(1-P_{N})
C
=
C
F
A
P
F
A
(
1
−
P
P
)
+
C
F
R
P
F
R
(
1
−
P
N
)
,
C F A C_{FA}
C
F
A
和
P F R P_{FR}
P
F
R
是代价因子。
3.DET曲线(detection error tradeoff):FA和FR的曲线
数据集
NIST SRE
RSR2015 Text-Dependent
VAD
短时能量:取20ms为一帧,然后用3高斯混合模型拟合,取
m m i d − α Σ m i d m_{mid}-\alpha\sqrt{\Sigma_{mid}}
m
m
i
d
−
α
Σ
m
i
d
作为分分界,来确定是否有声音。(
α \alpha
α
为经验值,通常取1.5到2,mid为中间高斯分量)
加权有限状态转移(WFST):用静音和一些说话声音训练一个HMM,然后进行VAD,缺点是需要标注数据。
特征
MFCC梅尔倒频系数:原理人耳对低频比高频敏感,流程signal-FFT-三角滤波器-DCT-MFCC
PLP感知线性预测:线性预测的系数(自相关)。
动态因子:MFCC和PLP都是对短时语音帧提取的特征,前后做差可以得到动态因子
高斯混合模型
对于一个
D D
D
维特征向量
x x
x
,混合概率密度定义为
p ( x ∣ λ ) = ∑ i = 1 M w i p i ( x ) , p(x|\lambda)=\sum_{i=1}^Mw_ip_i(x),
p
(
x
∣
λ
)
=
i
=
1
∑
M
w
i
p
i
(
x
)
,
是
M M
M
个unimodal(单峰) Gaussian densities
p i ( x ) p_i(x)
p
i
(
x
)
之和, 每个高斯分布的参数有一个
D × 1 D\times 1
D
×
1
维的均值向量
μ i \mu_i
μ
i
,和一个
D × D D\times D
D
×
D
维的协方差矩阵
Σ i \Sigma_i
Σ
i
:
p i ( x ) = 1 ( 2 π ) D / 2 ∣ Σ i ∣ 1 / 2 e x p [ − 1 2 ( x − μ i ) ′ ( Σ i ) − 1 ( x − μ i ) ] p_i(x)=\frac{1}{(2\pi)^{D/2}|\Sigma_i|^{1/2}}exp[{-\frac{1}{2}(x-\mu_i)'(\Sigma_i)^{-1}}(x-\mu_i)]
p
i
(
x
)
=
(
2
π
)
D
/
2
∣
Σ
i
∣
1
/
2
1
e
x
p
[
−
2
1
(
x
−
μ
i
)
′
(
Σ
i
)
−
1
(
x
−
μ
i
)
]
混合权重
w i w_i
w
i
满足
∑ i = 1 M w i = 1 \sum_{i=1}^Mw_i=1
∑
i
=
1
M
w
i
=
1
。模型记为
λ = { w i , μ i , Σ i } \lambda=\{w_i, \mu_i, \Sigma_i\}
λ
=
{
w
i
,
μ
i
,
Σ
i
}
, where
i = 1 , . . . , M i=1,…,M
i
=
1
,
.
.
.
,
M
.
这里我们把
Σ i \Sigma_i
Σ
i
限定为对角阵,这是因为对角阵有3个好处:1.full covariance GMM可以被更高阶的diagonal covariance GMM等效表示;2.diagonal-matrix GMMs计算效率更高,因为公式中有大量的求逆,转置之类的;3.根据经验,我们观察到对角矩阵GMM优于全矩阵GMM。
给定训练特征向量集,可以使用EM算法估计最大似然模型参数。
通常假设特征向量
X = { x 1 , . . . , x T } X=\{x_1,…, x_T\}
X
=
{
x
1
,
.
.
.
,
x
T
}
,之间是独立的,那么给定参数
λ \lambda
λ
下的似然概率为
l o g p ( X ∣ λ ) = ∑ t = 1 T l o g p ( x t ∣ λ ) , log~p(X|\lambda)=\sum_{t=1}^Tlog~p(x_t|\lambda),
l
o
g
p
(
X
∣
λ
)
=
t
=
1
∑
T
l
o
g
p
(
x
t
∣
λ
)
,
GMM-UBM
UBM是指根据所有说话人(有标签+没标签)训练出的高斯混合模型,作为说话人识别的先验分布。
在GMM-UBM系统中,我们通过使用说话人的训练语音和贝叶斯自适应的方法调整UBM的参数来推导出说话人模型。自适应方法的基本思想是通过更新UBM中训练好的参数来推导说话者的模型。这提供了说话人模型和UBM之间更紧密的耦合,这不仅比解耦模型产生更好的性能,而且评分更快速。
给定UBM和对应某个speaker的训练向量
X = x 1 , . . . , x T X={x_1,…, x_T}
X
=
x
1
,
.
.
.
,
x
T