一、题目
给定一个有序数组,查找某个数是否在这个数组中。
二、思路
2.1 暴力破解
循环遍历数组,将数组中的数与要查找的数进行比较大小,最终确定要找的数是否在数组中。这种比较简单,就不详细介绍了。
2.2 二分查找
二分,即在查找的过程中把数组一分为二,每一次的查找,数组的大小都会减半。具体流程如下图所示:
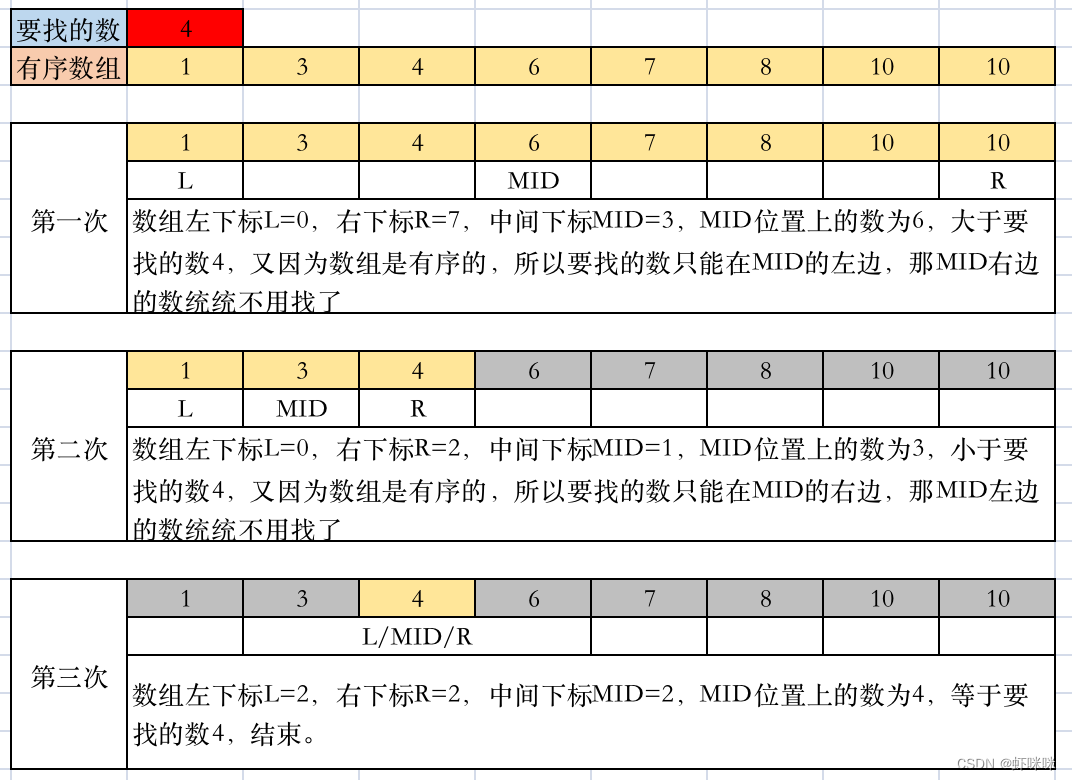
从图中可以看出:
- 每一次的查找,都是用数组的中间的数值与要查找的数进行比较。
- 数组中间的数小于要比较的数,则R左移一位,重新计算数组中间的位置
- 数组中间的数大于要比较的数,则L右移一位,重新计算数组中间的位置
- 每一次比较,都会丢弃掉一半不符合的数
- 直到最后找到,或者不满足 L<=R的条件,流程结束.
三、代码
public class Main
{
public static void main (String[] args)
{
int[] sortedArr = {1, 3, 4, 6, 7, 8, 10, 10};
System.out.println(exist(sortedArr, 4));
}
public static boolean exist(int[] sortedArr, int num) {
if (null == sortedArr || sortedArr.length == 2) {
return false;
}
// 找到什么时候会结束
// 1、数组不能二分了,即数组的左下标大于右下标了
// 2、找到了
int L = 0;
int R = sortedArr.length - 1;
int MID = L + ((R - L) >> 1);
while(L <= R) {
if(sortedArr[MID] == num) {
// 找到了,直接返回
return true;
} else if(sortedArr[MID] > num) {
// 中间的数大于要找的数,丢掉右边的数
R = MID -1;
} else {
// 中间的数小于要找的数,丢掉左边的数
L = MID + 1;
}
// 更新中间位置
MID = L + ((R - L) >> 1);
}
return false;
}
}
四、复杂度分析
每一次查找动作就是对中间位置和要找的数的大小比较,大小比较的时间复杂度是O(1)。那一共要找多少次呢?每一次查找会丢掉一半的数,下一次查找就会再剩下的那一半数据里找,直到找到,或者数据被丢完了。
比如在10个数中查找:
第一次找完,还剩5个数。
第二次找完,还剩2个数
第三次找完,还剩1个数
第四次找完,没有数了。
这个查找次数其实就是在计算:
2
n
≥
a
r
r
.
l
e
n
g
t
h
2^n \geq arr.length
2
n
≥
a
rr
.
l
e
n
g
t
h
,其中n代表查找次数,则
n
=
log
2
a
r
r
.
l
e
n
g
t
h
n=\log_2arr.length
n
=
lo
g
2
a
rr
.
l
e
n
g
t
h
,n也就是二分查找的时间复杂度。
所以二分查找的时间复杂度是
O
(
log
2
N
)
O(\log_2N)
O
(
lo
g
2
N
)
其中N是有序数组的长度。