微积分
求极限
函数极限
计算函数极限的形式:Limit [ expr, x->x0]
求下列极限
(1
)
lim
x
→
0
sin
(
a
x
)
x
\displaystyle(1) \lim _{x \rightarrow 0} \frac{\sin (a x)}{x}
(
1
)
x
→
0
lim
x
sin
(
a
x
)
(2
)
lim
x
→
1
(
m
1
−
x
m
−
n
1
−
x
n
)
\displaystyle(2) \lim _{x \rightarrow 1}\left(\frac{m}{1-x^{m}}-\frac{n}{1-x^{n}}\right)
(
2
)
x
→
1
lim
(
1
−
x
m
m
−
1
−
x
n
n
)

不是所有的函数都有确定的极限。例如
lim
x
→
0
sin
(
1
/
x
)
\displaystyle\lim_{x\to 0}\sin(1/x)
x
→
0
lim
sin
(
1
/
x
)
,极限不存在,在
0
0
0
附近,函数在
[
−
1
,
1
]
[-1, 1]
[
−
1
,
1
]
之间波动,Limit运算的结果是一个区间。

数列极限
数列的极限,可以用同样的形式进行计算。
计算数列的极限
(1
)
lim
n
→
∞
(
n
+
n
−
n
)
\displaystyle(1) \lim _{n \rightarrow \infty}(\sqrt{n+\sqrt{n}}-\sqrt{n})
(
1
)
n
→
∞
lim
(
n
+
n
−
n
)
(2
)
lim
n
→
∞
n
!
n
n
\displaystyle(2) \lim _{n \rightarrow \infty} \frac{n !}{n^{n}}
(
2
)
n
→
∞
lim
n
n
n
!

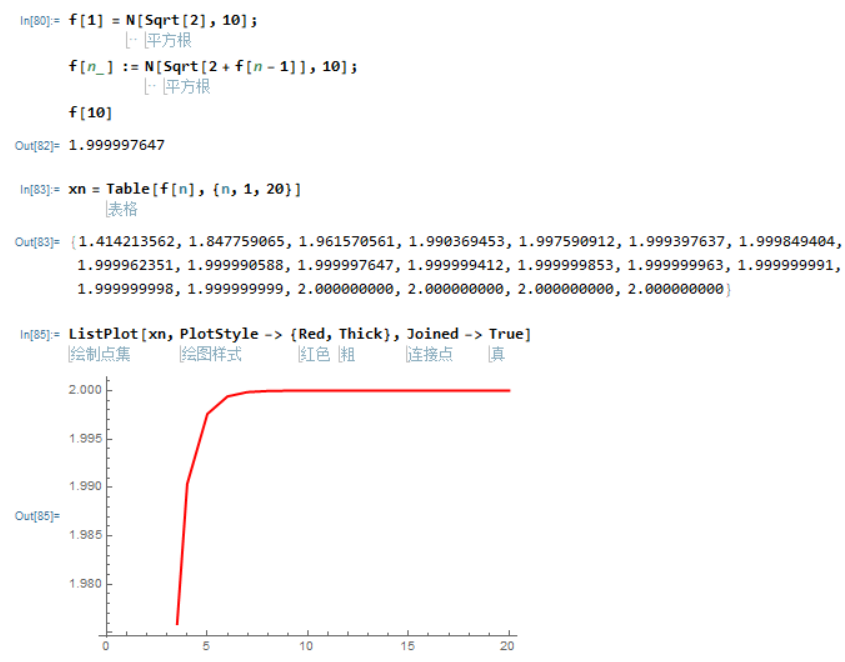
递归定义的数列极限
设
x1
=
2
,
x
n
=
2
+
x
n
−
1
,
x_1=\sqrt{2},x_n=\sqrt{2+x_{n-1}},
x
1
=
2
,
x
n
=
2
+
x
n
−
1
,
求
lim
n
→
∞
x
n
.
\displaystyle\lim_{n\to\infty}x_n.
n
→
∞
lim
x
n
.
单侧极限
Limit[expr, x -> x0]
计算 x → x0时函数 expr 的极限
Limit[expr, x -> x0, Direction -> 1]
计算x → x0时函数 expr 的左极限
Limit[expr, x -> x0, Direction -> -1]
计算x → x0时函数 expr 的右极限
计算下列极限:
(1
)
lim
x
→
0
+
log
(
x
)
x
\displaystyle(1) \lim _{
{x} \rightarrow 0^{+}} \frac{\log ({x})}{
{x}}
(
1
)
x
→
0
+
lim
x
lo
g
(
x
)
(2
)
lim
x
→
∞
Γ
(
x
+
1
2
)
x
Γ
(
x
)
\displaystyle(2) \lim _{
{x} \rightarrow \infty} \frac{\Gamma\left({x}+\frac{1}{2}\right)}{\sqrt{
{x}} \Gamma({x})}
(
2
)
x
→
∞
lim
x
Γ
(
x
)
Γ
(
x
+
2
1
)

累次极限
从 Mathematica 语言的语法上说,Limit 函数自己不带对多个变量取极限的功能即不能计算重极限,可以计算累次极限。
计算
lim
y
→
∞
lim
x
→
∞
(
x
y
x
2
+
y
2
)
x
2
\displaystyle\lim _{y \rightarrow \infty} \lim _{x \rightarrow \infty}\left(\frac{x y}{x^{2}+y^{2}}\right)^{x^{2}}
y
→
∞
lim
x
→
∞
lim
(
x
2
+
y
2
x
y
)
x
2

还可以计算自变量沿某一固定路径趋向于固定点时,表达式的极限
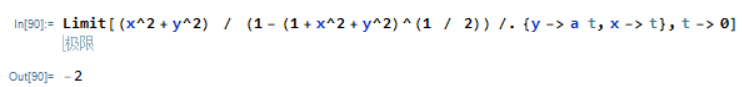
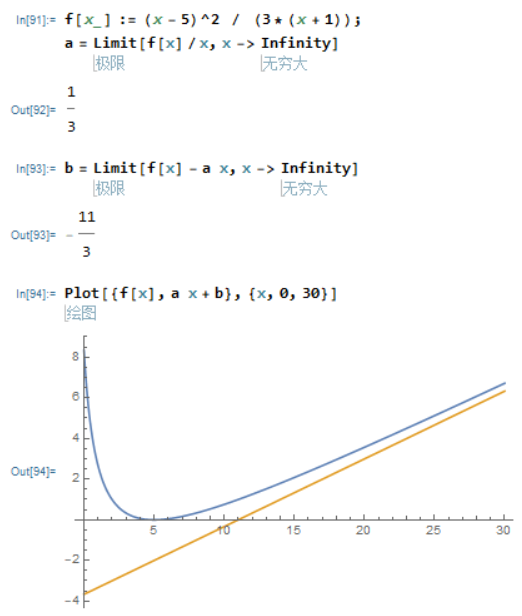
渐近线
画出函数
f(
x
)
=
(
x
−
5
)
2
3
(
x
+
1
)
\displaystyle f(x)=\frac{(x-5)^2}{3(x+1)}
f
(
x
)
=
3
(
x
+
1
)
(
x
−
5
)
2
的斜渐近线。
函数f(x)的渐近线是指:当
x
→
∞
x\to\infty
x
→
∞
时,
f
(
x
)
f(x)
f
(
x
)
无限接近某一直线
y
=
x
+
b
y=x+b
y
=
x
+
b
即
lim
x
→
∞
(
f
(
x
)
−
(
a
x
+
b
)
)
=
0
\displaystyle\lim_{x\to\infty} (f(x)-(a x+b))=0
x
→
∞
lim
(
f
(
x
)
−
(
a
x
+
b
)
)
=
0
,需要用极限的思想确定参数a和b的值。
微商和微分
微商(导数)
计算导数的命令是
D[f, x]
和
D[f, {x, n}]
,分别表示
f
′
(
x
)
f'(x)
f
′
(
x
)
和
f
(
n
)
(
x
)
f ^{(n)}(x)
f
(
n
)
(
x
)
。
计算导数和偏导数是同一命令。
如果
f
f
f
是一元函数,
D[f, x]
表示
d
f
d
x
\dfrac{
{\rm d}f}{
{\rm d}x}
d
x
d
f
;如果
f
f
f
是多元函数,
D[f, x]
表示
∂
f
∂
x
\dfrac{\partial f}{\partial x}
∂
x
∂
f
微商函数的常用形式如下:
| D[f, x] |
偏导数 ∂ f ∂ x \dfrac{\partial f}{\partial x} ∂ x ∂ f |
| D[f, x1, x2, …, xn] |
高阶偏导数 ∂ n f ∂ x 1 ∂ x 2 … ∂ x n \dfrac{\partial^{n} f}{\partial x_1 \partial x_ 2 \ldots \partial x_ n} ∂ x 1 ∂ x 2 … ∂ x n ∂ n f |
| D[f, {x, n}] |
n n n 阶导数 ∂ n f ∂ x n \dfrac{\partial ^n f}{\partial x^n} ∂ x n ∂ n f |
| D[f, x, NonConstants → {y1, y2, …, ym}] |
复合函数偏导数 ∂ f ∂ x , y 1 , ⋯ , y m \dfrac{\partial f}{\partial x},y_1,\cdots,y_m ∂ x ∂ f , y 1 , ⋯ , y m 是 x x x 的函数 |
|
D[f, { {x, y, z, …}}] |
偏导向量 ( ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z , … ) \left(\dfrac{\partial {f}}{\partial {x}}, \dfrac{\partial {f}}{\partial {y}}, \dfrac{\partial {f}}{\partial {z}}, \ldots\right) ( ∂ x ∂ f , ∂ y ∂ f , ∂ z ∂ f , … ) |
求函数
f(
x
)
=
sin
(
x
2
+
x
)
f(x)=\sin \left(x^2+\sqrt{x}\right)
f
(
x
)
=
sin
(
x
2
+
x
)
在
x=
2
x = 2
x
=
2
处的导数

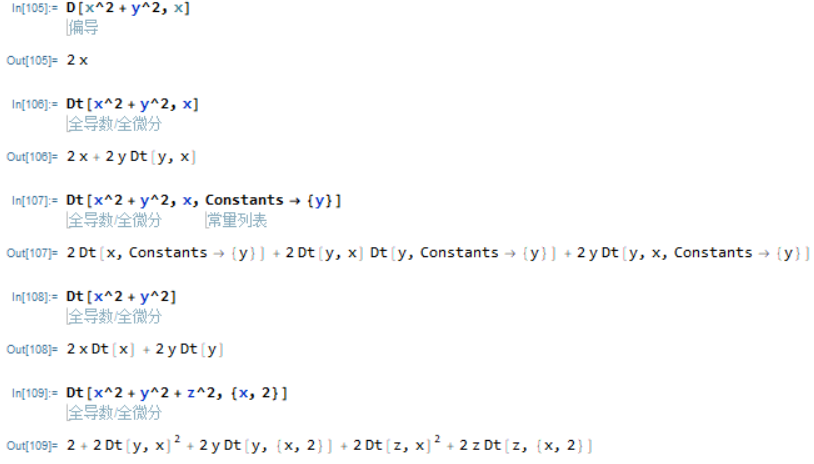
全微分
在Mathematica中,
D[f, x]
计算变量为 f 关于 x 的偏导数,系统默认f 中的其它变量与 x无关;
Dt[f]
给出f的全微分形式
Dt[f, x]
给出f的全导数,系统默认 f 中所有变量是 x 的函数。
对于f中不依赖于 x 的常量,要用选项 Constants -> {常量1, 常量2, …} 作出说明。
x,
y
x, y
x
,
y
的函数关系由参数方程
x=
2
t
2
,
y
=
sin
(
t
)
x = 2 t ^2, y = \sin(t)
x
=
2
t
2
,
y
=
sin
(
t
)
确定,求
yy
y
关于
xx
x
的二阶导数。

不定积分和定积分
不定积分
计算不定积分的命令是
Integrate[f, x]
,输出结果中省略积分常数。
计算二重积分的命令是
Integrate[f, x, y]
,积分的顺序是从右自左,先对变量y做积分计算,再对变量x做积分计算
Integreate主要计算只含有 “简单函数” 的被积函数。“简单函数” 包括有理函数、指数函数、对数函数、三角和反三角函数。
计算下列不定积分
(1
)
∫
3
a
x
2
d
x
\displaystyle(1) \int 3 {ax}^{2} \mathrm{d} {x}
(
1
)
∫
3
a
x
2
d
x
(2
)
∫
x
2
−
a
2
d
x
\displaystyle(2) \int \sqrt{x^{2}-a^{2}} \mathrm{d} x
(
2
)
∫
x
2
−
a
2
d
x
(3
)
∫
cos
x
d
x
\displaystyle(3) \int \sqrt{\cos x} \mathrm{d} x
(
3
)
∫
cos
x
d
x
(4
)
∫
1
1
+
x
4
d
x
\displaystyle(4) \int \frac{1}{1+x^{4}} \mathrm{d} x
(
4
)
∫
1
+
x
4
1
d
x

Integrate可以计算形式上的积分
∫e
x
(
f
(
x
)
+
f
′
(
x
)
)
d
x
\displaystyle\int e^x(f(x)+f'(x)) \mathrm{d} x
∫
e
x
(
f
(
x
)
+
f
′
(
x
)
)
d
x

Integrate可以计算分段函数积分
f(
x
)
=
{
x
x
⩾
1
1
x
<
1
f(x)=\begin{cases}x \qquad x\geqslant1\\1\qquad x<1\end{cases}
f
(
x
)
=
{
x
x
⩾
1
1
x
<
1
,求
∫f
(
x
)
d
x
\displaystyle\int f(x) \mathrm{d} x
∫
f
(
x
)
d
x

Mathematica可以对向量值函数积分

Mathematica提供如Bessel函数、Gamma函数 和Beta函数等二三十个数学物理特殊函数可以用来表示积分结果。
∫e
−
x
2
d
x
\displaystyle\int e^{-x^2} \mathrm{d} x
∫
e
−
x
2
d
x

Mathematica算不出结果的积分对被积函数做些化简外仍按Integrate形式输出

定积分
Integrate[f[x], {x, a, b}]
,可以计算
∫
a
b
f
(
x
)
d
x
\displaystyle\int _a^b f(x) \mathrm{d} x
∫
a
b
f
(
x
)
d
x
的准确解
NIntegrate[f[x], {x, a, b}]
,可以计算
∫
a
b
f
(
x
)
d
x
\displaystyle\int _a^b f(x) \mathrm{d} x
∫
a
b
f
(
x
)
d
x
的数值解

多重积分
Integrate [f, {x, a, b}, {y, c, d}]
,计算累次积分
∫
a
b
d
x
∫
c
d
f
(
x
,
y
)
d
y
\displaystyle\int _a^b \mathrm{d} x\int_c^df(x,y)\mathrm{d} y
∫
a
b
d
x
∫
c
d
f
(
x
,
y
)
d
y
的准确解.
NIntegrate [f, {x, a, b}, {y, c, d}]
,计算累次积分
∫
a
b
d
x
∫
c
d
f
(
x
,
y
)
d
y
\displaystyle\int _a^b \mathrm{d} x\int_c^df(x,y)\mathrm{d} y
∫
a
b
d
x
∫
c
d
f
(
x
,
y
)
d
y
的数值解.
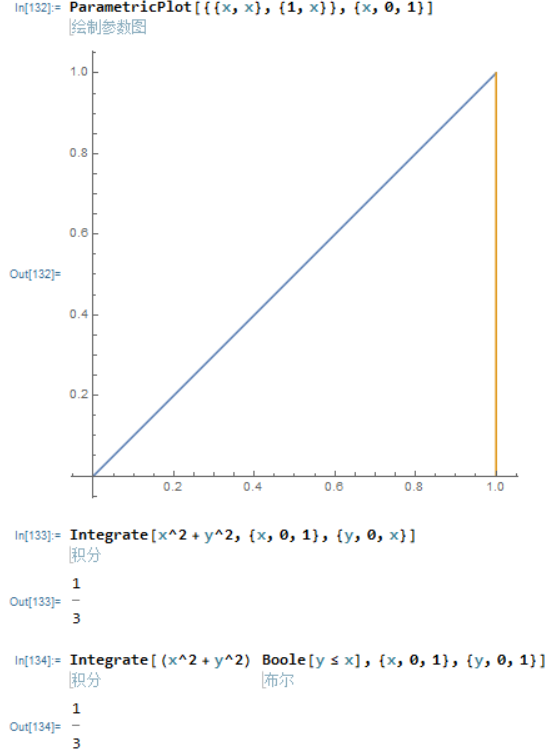
计算区域
DD
D
上的二重积分 ,
DD
D
由
y=
x
y = x
y
=
x
以及
xx
x
轴,
x=
1
x = 1
x
=
1
围成.
∬D
sin
(
x
+
2
y
)
d
x
d
y
\displaystyle \iint_D\sin(x+2y) \mathrm{d} x\mathrm{d} y
∬
D
sin
(
x
+
2
y
)
d
x
d
y
计算
∭V
x
y
2
z
3
d
x
d
y
d
z
,
\displaystyle\iiint_Vxy^2z^3\mathrm{d} x\mathrm{d} y\mathrm{d} z,
∭
V
x
y
2
z
3
d
x
d
y
d
z
,
其中
VV
V
是由曲面
z=
x
y
,
z
=
0
,
y
=
x
,
x
=
1
z = xy, z = 0, y = x, x = 1
z
=
x
y
,
z
=
0
,
y
=
x
,
x
=
1
围成。
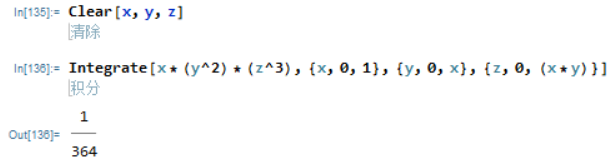
计算两个圆柱体
x2
+
y
2
=
1
,
x
2
+
z
2
⩽
1
x^2+y^2=1,x^2+z^2\leqslant 1
x
2
+
y
2
=
1
,
x
2
+
z
2
⩽
1
相交部分的体积。

计算曲线积分
∫L
x
2
+
x
cos
x
d
s
,
L
\displaystyle\int _L x^2+x\cos x \mathrm{d} s,L
∫
L
x
2
+
x
cos
x
d
s
,
L
是单位圆。

计算单位球面面积

级数
幂级数展开
Series[expr, {x, x0, n}]
将expr在x = x0点展开到n阶的幂级数
Series[expr, {x, x0, n}, {y, y0, m}]
先对y展开到m阶再对x展开n阶幂级数
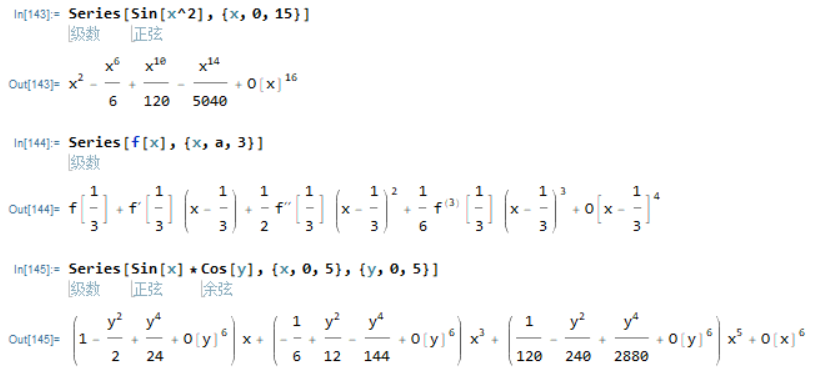
展开式中可能将分数指数,对数函数等作为基本元素。

Series命令可以计算无界函数在瑕点的洛朗展开式,展开式的最高次数可以是负数。

Series命令可以计算函数在无穷远点的洛朗展开式
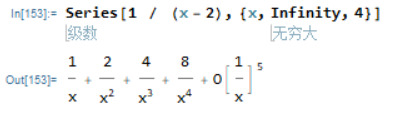
幂级数计算
幂级数求和

无穷乘积
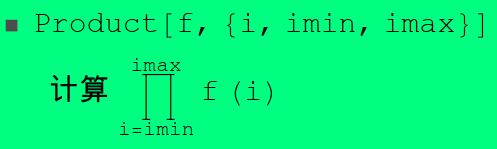

求幂级数
∑n
=
0
∞
x
4
n
+
1
4
n
+
1
\displaystyle\sum_{n=0}^{\infty}\frac{x^{4n+1}}{4n+1}
n
=
0
∑
∞
4
n
+
1
x
4
n
+
1
的收敛域与和函数。

检查端点是否收敛

两个端点都是发散点。收敛域(-1,1)

给出幂级数中某一项的系数
SeriesCoefficient[f, n]
级数f中x^n的系数
SeriesCoefficient[f, {x, x0, n}]
函数f在x0的展开式中 (x – x0)^n的系数

反函数级数
InverseSeries[s, {x, x0, n}]
给出级数s的反函数的幂级数展开式

幂级数复合
ComposeSeries[s1, s2]
表示用幂级数s2代换幂级数s1中的变量x

Fourier级数

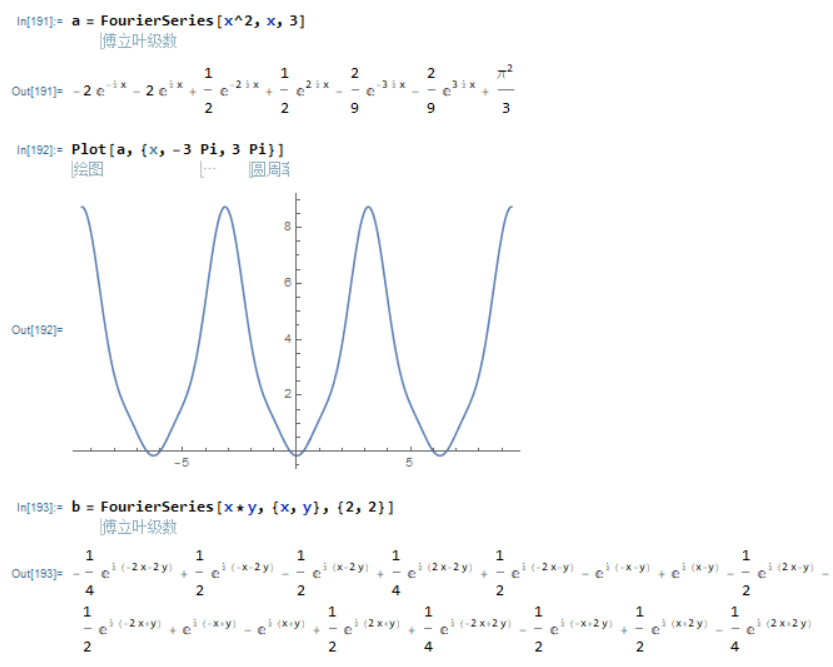
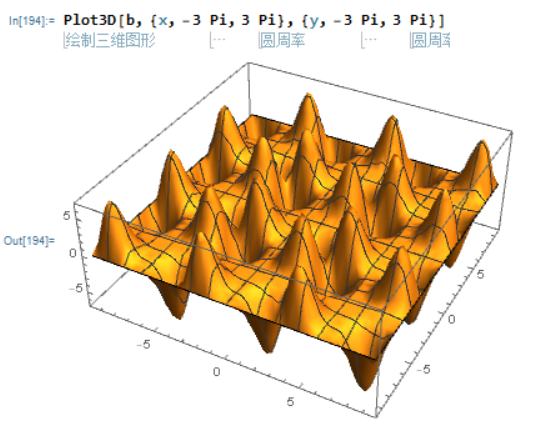
对于以2L为周期的函数,要用
FourierParameters->{1,2Pi/L}
说明

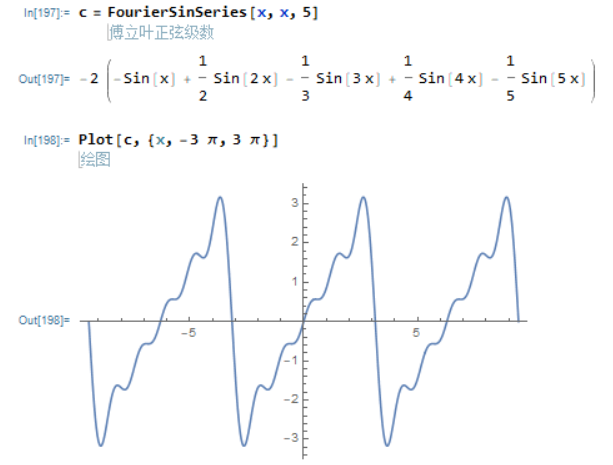
正弦级数与余弦级数
FourierSinSeries[f[x], x, n]
f[x]是以2π为周期的函数,在[-π,π]上是奇函数
FourierCosSeries[f[x], x, n]
f[x]是以2π为周期的函数,在[-π,π]上是偶函数
若函数周期不是2π,同样用
FourierParameters
说明
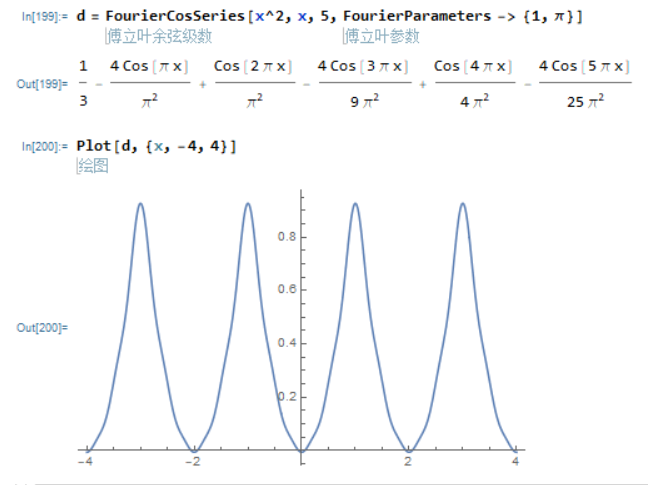
微分方程
求解常微分方程
求解常微分方程和常微分方程组的一般形式:
DSolve[eqns, y[x], x]
解y(x)的微分方程或方程组 eqns,x为变量。
DSolve[eqns, y, x]
在纯函数的形式下求解
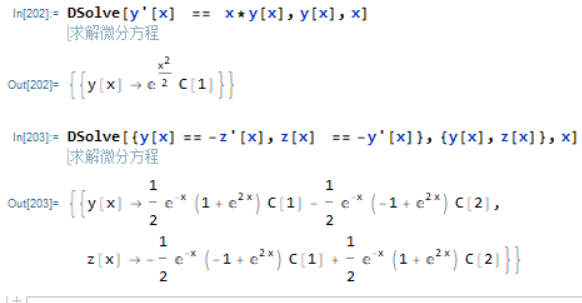
一般一个一阶线性微分方程都可以通过积分运算求解,但是如果方程的个数大于1,或阶数大于2,求解就没有固定的方法,一些简单的二阶线性方程的解被当做特殊函数来表示其它方程的解。

一些特殊类型的二阶线性微分方程可能有形式简单的解
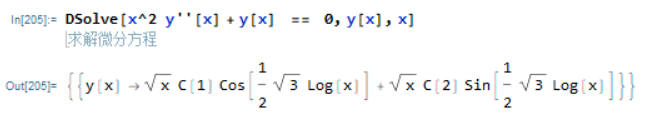
三阶以上的方程只有极少的方程能够被解出
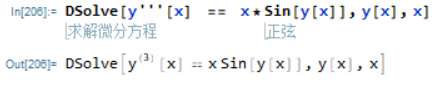
求解初值问题
(1
+
x
2
)
y
′
′
+
2
x
y
′
−
6
x
2
−
2
=
0
,
y
(
−
1
)
=
0
,
y
′
(
−
1
)
=
0
\left(1+x^{2}\right) y^{\prime \prime}+2 x y^{\prime}-6 x^{2}-2=0, y(-1)=0, y^{\prime}(-1)=0
(
1
+
x
2
)
y
′
′
+
2
x
y
′
−
6
x
2
−
2
=
0
,
y
(
−
1
)
=
0
,
y
′
(
−
1
)
=
0
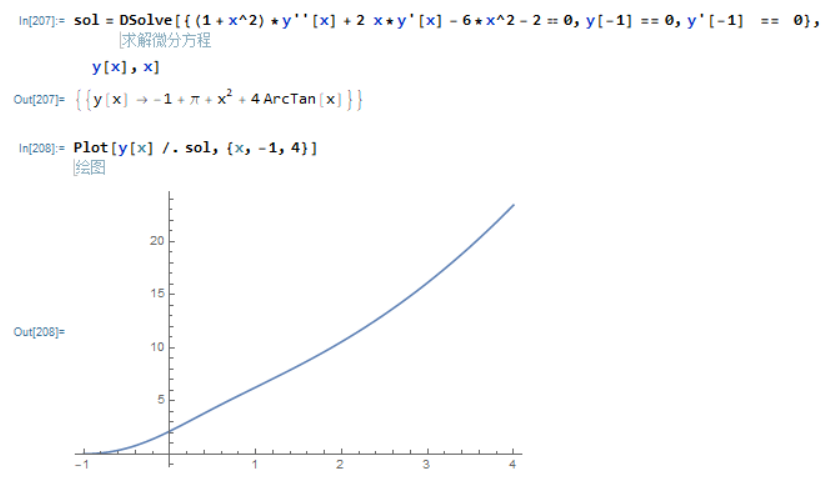
纯函数形式的解可以代入微分的运算
DSolve[eqns,y,x]
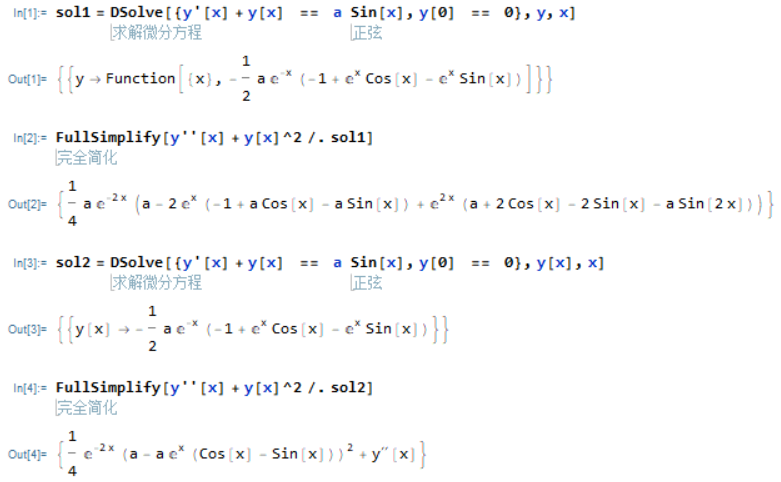
求解偏微分方程
求解偏微分方程的命令是
DSolve[eqn, y, {x1, x2, ..}]
DSolve[eqns, {y1,y2,..}, {x1, x2, ..}]
求解偏微分方程
∂y
(
x
1
,
x
2
)
∂
x
1
+
∂
y
(
x
1
,
x
2
)
∂
x
2
=
1
x
1
x
2
\frac{\partial y({x} _1, {x} _2)}{\partial {x} _1}+\frac{\partial y({x} _1, {x} _2)}{\partial {x} _2}=\frac{1}{
{x}_ 1x_2}
∂
x
1
∂
y
(
x
1
,
x
2
)
+
∂
x
2
∂
y
(
x
1
,
x
2
)
=
x
1
x
2
1
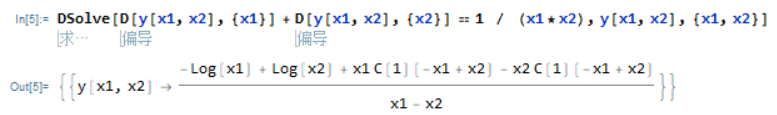
求解调和方程
ux
x
+
u
y
y
=
0
u_{xx}+u_{yy}=0
u
x
x
+
u
y
y
=
0

参考资料