快速傅里叶变换(FFT)利用了旋转因子
e
−
j
2
π
N
e^{-j \frac{2 \pi}{N}}
e
−
j
N
2
π
的周期性、共轭对称性以及可约性极大简化了DFT的计算量,具体可以查阅清华大学出版社数字信号处理程佩青第四版第四章。
理论推导一大堆,最重要的是对于蝶形图的理解。书上有8点的蝶形图,这里给出16点的蝶形图。
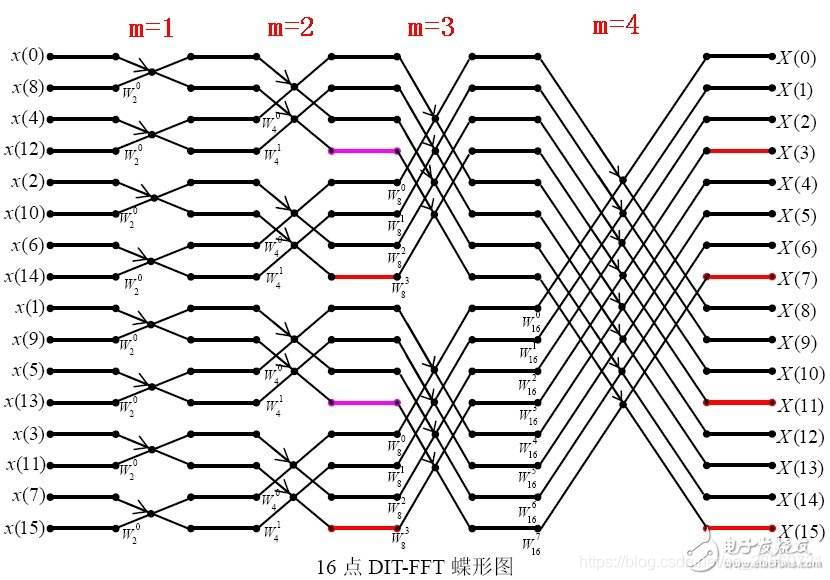
这张图其实有点小问题,所有的横线都画漏了。
下面讨论C语言实现,此处实现DIT的基2 FFT算法。分为两步,
第一步
是对于输入序列的重新排序,以确保输出的频域值是顺序的;
第二步
是进行复数的乘法和加法,每一个蝶形需要两次复数加法(其实是一次加一次减)以及一次复数乘法。输入的点个数必须是2的幂次,如果不是,需要补0让输入点数满足2的幂次。
第一步采用Rader算法,就是将一个数转化成倒位序。以8点为例:
| 原序列 | FFT序列 | 原序列二进制(i) | FFT序列二进制(j) |
|---|---|---|---|
| 0 | 0 | 000 | 000 |
| 1 | 4 | 001 | 100 |
| 2 | 2 | 010 | 010 |
| 3 | 6 | 011 | 110 |
| 4 | 1 | 100 | 001 |
| 5 | 5 | 101 | 101 |
| 6 | 3 | 110 | 011 |
| 7 | 7 | 111 | 111 |
从表中可以看出,要将输入序列换成需要的FFT序列,则只需要将原序列的二进制表示倒过来就可以了。(当初我发现这一点时惊呆了!)
设输入点数为N,则蝶形的级数为
t
=
log
2
N
t=\log_2N
t
=
lo
g
2
N
,表示序列的2进制位数也是t位。
Rader算法实现原理是:i,j都从0开始,若已知某个倒位序j,要求下一个倒位序数,则应先判断j的最高位是否为0,将j与k=N/2相比较,如果k>j,则j的最高位为0,只要把该位变为1(j与k=N/2相加即可),就得到下一个倒位序数;如果k<=j,则j的最高位为1,可将最高位变为0(j与k=N/2相减即可)。然后还需判断次高位,这可与k=N/4相比较,若次高位为0,则需将它变为1(加N/4即可)其他位不变,既得到下一个倒位序数;若次高位是1,则需将它也变为0。然后再判断下一位,以此类推。
C语言实现:
nv2=FFT_N/2; //变址运算,即把自然顺序变成倒位序,采用雷德算法
nm1=FFT_N-1;
for(i=0;i<nm1;i++)
{
if(i<j) //如果i<j,即进行变址
{
t=xin[j];
xin[j]=xin[i];
xin[i]=t;
}
k=nv2; //求j的下一个倒位序
while(k<=j) //如果k<=j,表示j的最高位为1
{
j=j-k; //把最高位变成0
k=k/2; //k/2,比较次高位,依次类推,逐个比较,直到某个位为0
}
j=j+k; //把0改为1
}
再给出一种实现方式,利用按位与来实现。
void change()
{
complex temp;
unsigned short i=0,j=0,k=0;
double t;
for(i=0;i<size_x;i++)
{
k=i;j=0;
t=(log(size_x)/log(2)); //级数
while((t--)>0) //利用按位与以及循环实现码位颠倒,循环t次,t--是先判断再自减,--t是先自减再判断
{
j=j<<1; //将找到的1移位来实现倒序
j|=(k & 1); //对于t级的蝶形,这里的操作数也是t位,判断k的末位是不是1,如果是的话将j的末位置位1
//将k的每一位遍历一遍找1
k=k>>1;
}
if(j>i) //将x(n)的码位互换,其实只需要循环size_x/2次就行了(待考证),因为i>size_x/2时,倒序必定比i小。
{
temp=x[i];
x[i]=x[j];
x[j]=temp;
}
}
output();
}
接下来是蝶形运算的处理
这里以8点FFT为例子,放上一张图片:
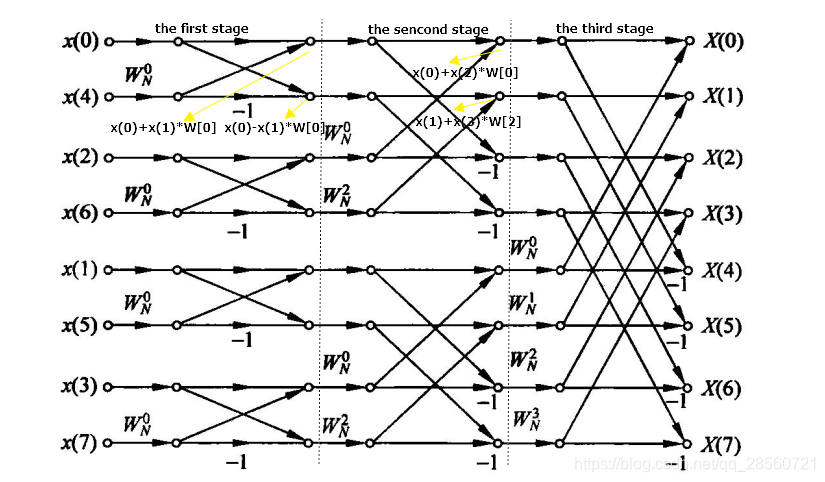
再放上FFT核心C代码:
void fft()
{
int i=0,j=0,k=0,l=0;
complex up,down,product;
change(); //调用变址函数
for(i=0;i< log(size_x)/log(2) ;i++) /*一级蝶形运算 stage */
{
l=1<<i;
for(j=0;j<size_x;j+= 2*l ) /*一组蝶形运算 group,每个group的蝶形因子乘数不同*/
{
for(k=0;k<l;k++) /*一个蝶形运算 每个group内的蝶形运算*/
{
mul(x[j+k+l],W[size_x*k/2/l],&product);
add(x[j+k],product,&up);
sub(x[j+k],product,&down);
x[j+k]=up;
x[j+k+l]=down;
}
}
}
}
N个点的FFT的级数可以划分为
log
2
N
\log_2N
lo
g
2
N
级,我们这里的8个点就是3级。我们计算FFT结果的过程其实就是将x[0]->x[7]完成三级蝶形运算的过程,通过三重循环实现,每一重循环完成一级的运算。例如在图上已经标注出来的,第一级运算之后x[0]变成了x[0]+x[1]*W[0],把新x[0]再带入下一级的运算中。**当然了,在第一级运算开始之前,你需要change函数完成倒序;还需要表示出旋转因子W
N
i
_N^i
N
i
。
我还手写了一份上述C代码循环执行过程,帮助理解:
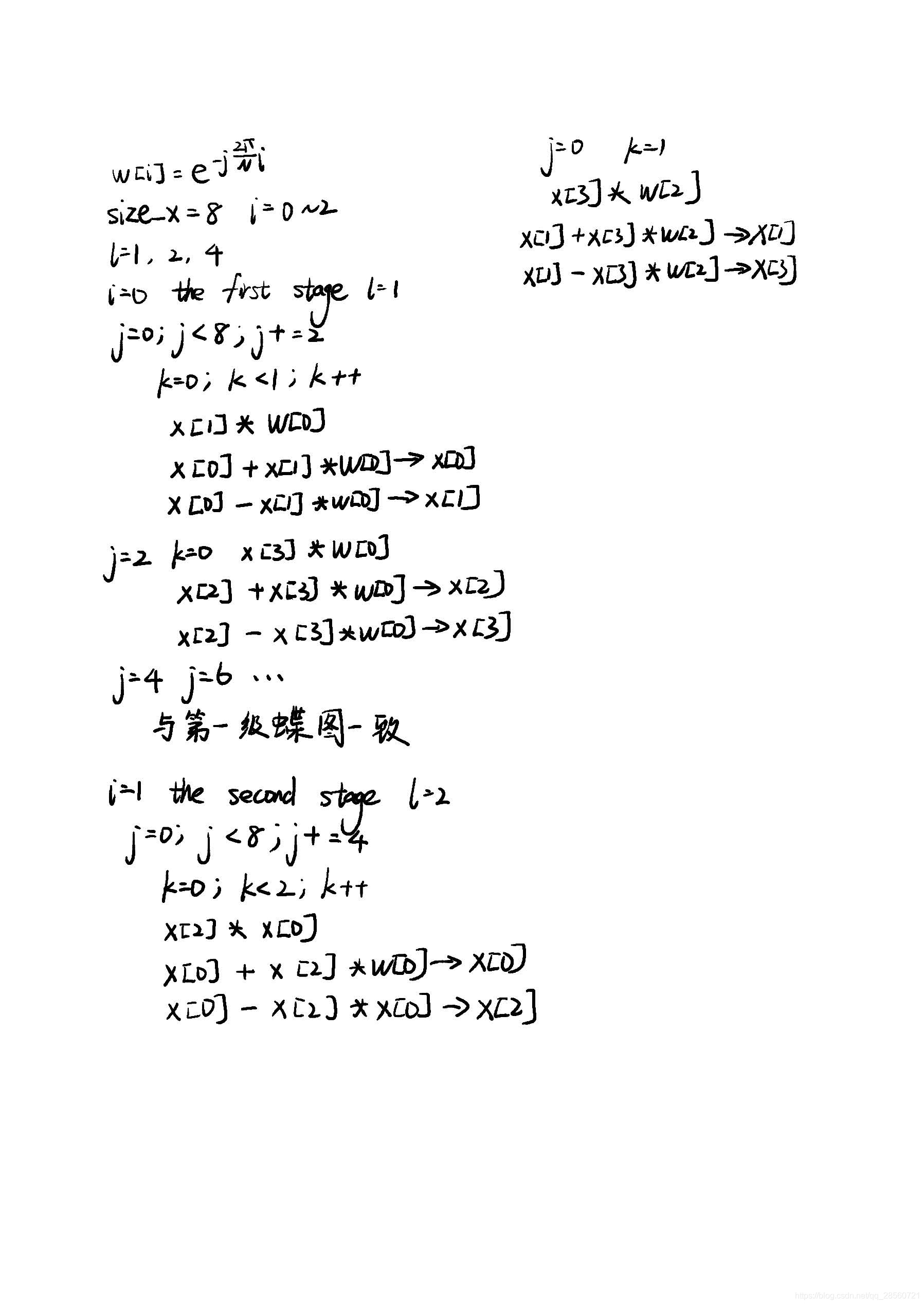
小结一下,DFT是DTFT的离散形式,FFT是DFT的计算方法,FFT只是一个算系数的过程。