博客

题目描述：
给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中，每个数是它左上方和右上方的数的和。
例：

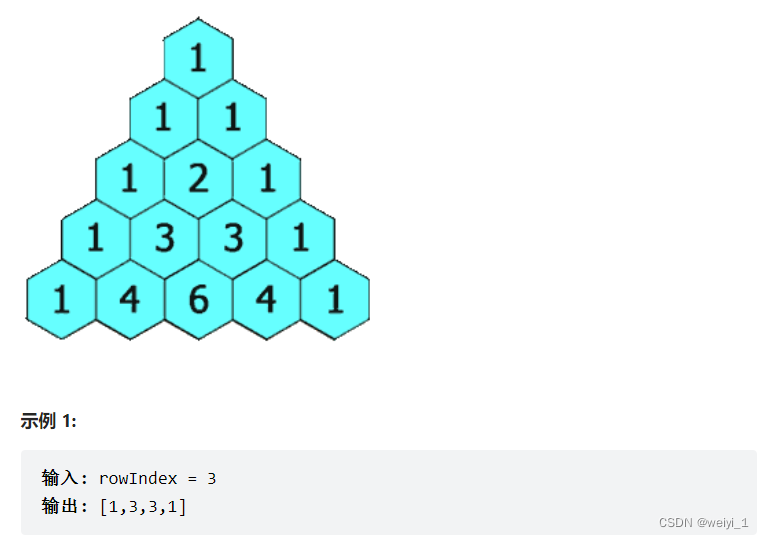
分析：是杨辉三角的拓展题型。
思路1：还是杨辉三角的做法，返回第rowIndex行即可。
代码：

 public List<Integer> getRow(int rowIndex) {
        List<List<Integer>> integers = new ArrayList<>();
        int sum;
        for (int i=0;i<=rowIndex;i++){
            ArrayList<Integer> integers1 = new ArrayList<>();
            for (int j=0;j<=i;j++){
                if (j==0||j==i){
                    integers1.add(1);
                }
                if(j>0 && j<i){
                    sum = integers.get(i-1).get(j-1)+ integers.get(i-1).get(j);
                    integers1.add(sum);
                }
            }
            integers.add(integers1);
        }
        return integers.get(rowIndex);
    }

结果：

结果分析：
这里时间复杂度为O(n^2)，利用了两次循环。所以阶梯会慢一点，执行用时2ms。
思路2：
直接算该行的数组。找规律，得到的是第1个元素和第n的元素为“1”。
规律是第 i 个元素为｛（i-1）的元素的值*（rowIndex-i+1）/ 2｝
代码：

public List<Integer> getRow(int rowIndex) {
        List<Integer> integers = new ArrayList<>();
        if(rowIndex == 0){
            integers.add(1);
            return integers;
        }
        for(int i = 0;i<=rowIndex;i++){
            if(i==0||i==rowIndex){
                integers.add(1);
            }
            if(i>0&&i<rowIndex){
                integers.add(integers.get(i-1)*(rowIndex-i+1)/i);
            }
        }
        return integers;
    }

但是结果却是错误的，如图所示：

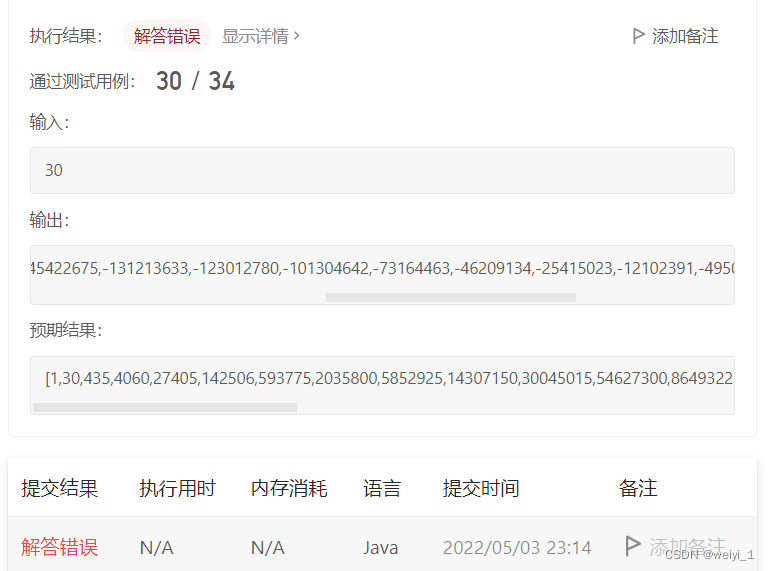
有负数的情况出现，是 int 类型不够用了，尝试采用Long类型的进行试验。
代码：

public List<Integer> getRow(int rowIndex) {
        List<Integer> integers = new ArrayList<>();
        if(rowIndex == 0){
            integers.add(1);
            return integers;
        }
        for(int i = 0;i<=rowIndex;i++){
            if(i==0||i==rowIndex){
                integers.add(1);
            }
            if(i>0&&i<rowIndex){
                integers.add((int)((long)integers.get(i-1)*(rowIndex-i+1)/i));
            }
        }
        return integers;
    }

结果如下：