文章目录
引言
-
研究数值解法的必要性


- 线性代数方程组的常用解法
-
直接法
只包含
有限次四则运算
。在计算过程中不发生舍入误差的假定下,计算结果就是原方程组的精确解。(适用于
小规模的n阶稠密
线性方程组) -
迭代法
从解的某个近似值出发,通过构造一个无穷序列去逼近精确解的方法(一般有限步内得不到精确解)。实现这一极限过程每一步的结果是把前一步所得的结果施行相同的演算步骤得到的。(适用于
大规模的n阶稀疏
线性方程组)
Remark
:由于运算过程中舍入误差的存在,实际上
直接方法得到的解也是方程组的近似解。
一、预备知识
1.1 矩阵基本运算和和行列式

1.2 矩阵的特征值和谱半径
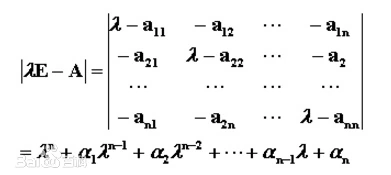
设A是n阶方阵,如果数λ和n维非零列向量x使关系式Ax=λx成立,那么这样的数λ称为矩阵A特征值,非零向量x称为A的对应于特征值λ的特征向量。
-
特征值性质

tr
(
A
)
tr(A)
t
r
(
A
)
为A 的
迹
。

-
注意

-
谱半径
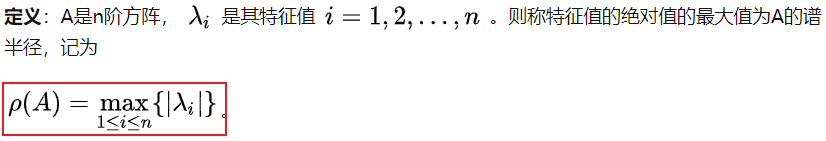
习题
1.3 特殊矩阵

-
对称正定矩阵

二、Gauss消去法
-
方程组的矩阵表示

高斯消元的基本思想:
将矩阵A的下三角部分消为零,即化为上三角形
2.1 不消主元的Gauss消去法
首先将方程组
Ax=b
化为
上三角方程组
,此过程称为
消去过程
,再求解上三角方程组,此过程称为
回代过程
.
例.
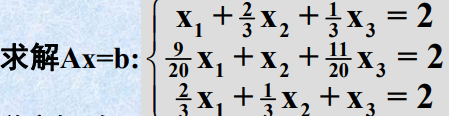


总结:Gauss消去法解Ax=b分两步:
消元
、
回代
.
-
不消主元的Gauss消去法
将方程组Ax=b的系数矩阵与右端项合并为:

第一步:

第二步:

第k步:

第n-1步:


回代:

-
定理


2.2 高斯主元素消去法
在计算过程中的舍入误差增大能得到控制,该方法就是稳定的。
小主元
是不稳定的根源,这就需要采用“选主元素”技术,即选取
绝对值最大的元素
作为
主元
。
1. Gauss列主元消去法
a
k
k
(
k
)
a_{kk}^{(k)}
a
k
k
(
k
)
称为第k步的主元

-
Gauss列主元消去法:
第一步:在第一列中选取最大值的元素,并将该行
ai
,
1
a_{i,1}
a
i
,
1
与第一行
a1
,
1
a_{1,1}
a
1
,
1
进行交换。(若该列中第一行
a1
,
1
a_{1,1}
a
1
,
1
最大,无需交换)


第k步:设第 步将增广矩阵(A,b)已化为


结论:当
kk
k
从
11
1
变化到
n−
1
n-1
n
−
1
时,
(A
,
b
)
(A,b)
(
A
,
b
)
成为上三角形式,再用回代公式求
xx
x
.
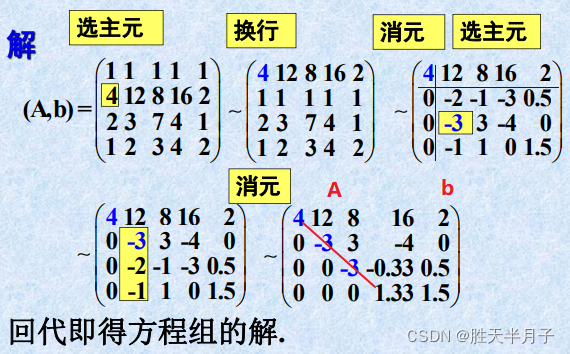
例. 用
Gauss列主元
解方程组
2. Gauss全主元消去法
概念不好理解,直接上例题+解析。
例.


通常用列主元消去法。
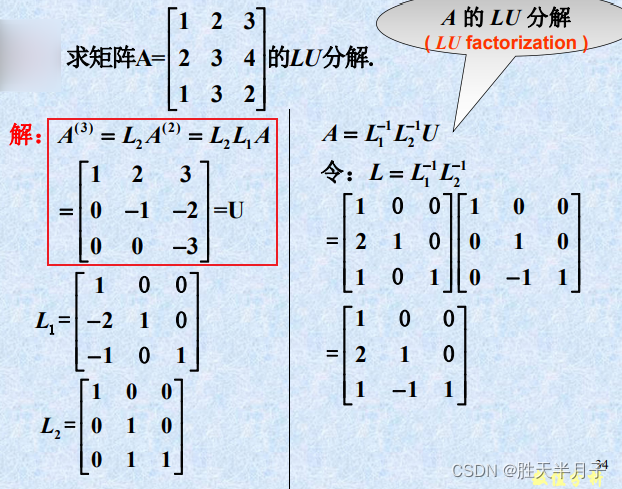
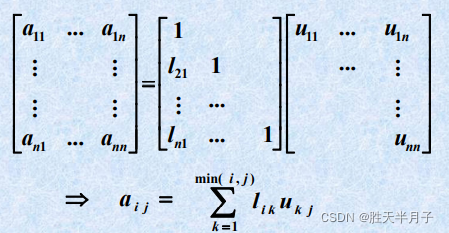
三、矩阵的三角分解法
3.1 用直接三角分解法求解方程组
-
高斯消元与LU分解的等价性
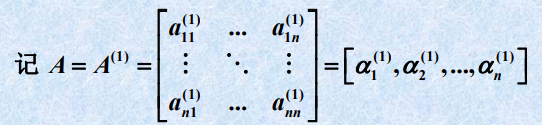
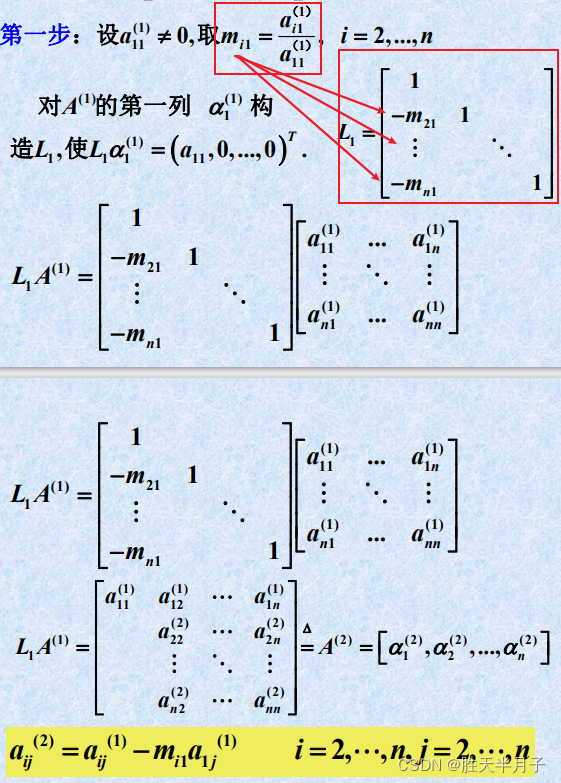
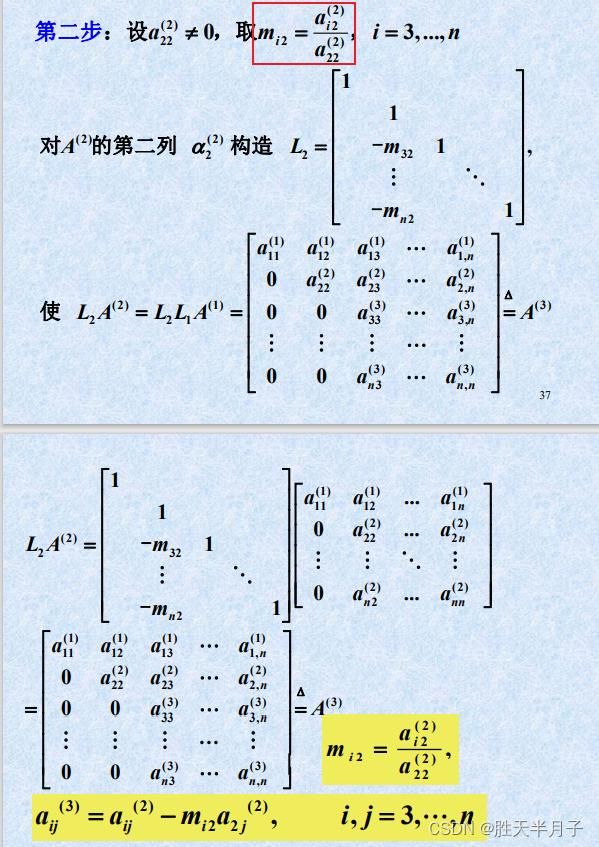



-
L与U
⭐⭐

-
矩阵三角分解的基本定理


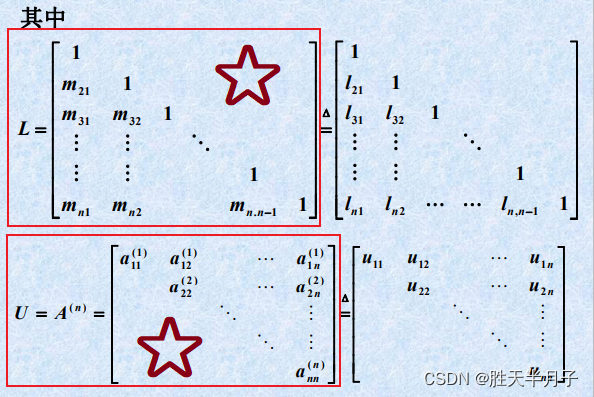
3.2 Doolittle分解法(杜利特尔)
-
一般计算公式⭐


习题
题目
-
例题
-
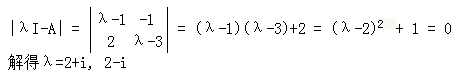
谱半径,就是
特征值绝对值(复数取模)中的最大值
,先求特征值。再取模,分别得到√5,√5,因此谱半径是√5。 -


-
例题