一、左式堆存在的意义
除了标准的插入和删除操作,堆结构在实际应用中的另一个常见的操作是
合并
,即将堆A和堆B重新组织成一个堆。若采用最基本的完全二叉堆数据结构,其最高效的实现策略是采用Floyd建堆算法将堆A和堆B直接重构成一个新堆,但是该算法的时间复杂度为O(n),这种性能在实际中不让人满意,而左式堆结构能保证在合并操作中只需要调整很少的点,所以能保证合并操作的时间复杂度低至O(logn)。而且基于合并操作,其插入删除操作也可以足够的高效,均为O(logn)。
左式堆: 左式堆(leftist heap)是优先级队列的另一种实现方式,可高效地支持堆合并操作。其基本思路:
在保持堆序性的前提下附加新的条件,使得在堆的合并过程中,只需调整很少量的节点,具休地,需参与调整的节点不超过O(logn)个,故可达到极高的效率
。
二、左式堆的结构
左式堆的整体结构呈单侧倾斜状,其中节点的分布均偏向左侧
,也链是说,
左式堆将不再如完全二又堆那样满足结构性,但事实上这无伤大雅,毕竟堆序性才是堆结构的关键条件,而结构性只不过是堆的一项附加条件
,正如稍后将要看到的,在将平衡性替换为左倾性之后,左式推结构的merge()操作乃至insert()和delMax()操作均可以高效地实现。
左式堆的为实现倾斜,借鉴了AVL树和红黑树技巧,为各节点引入“空节点路径长度”指标,并依此确定相关算法的执行方向。
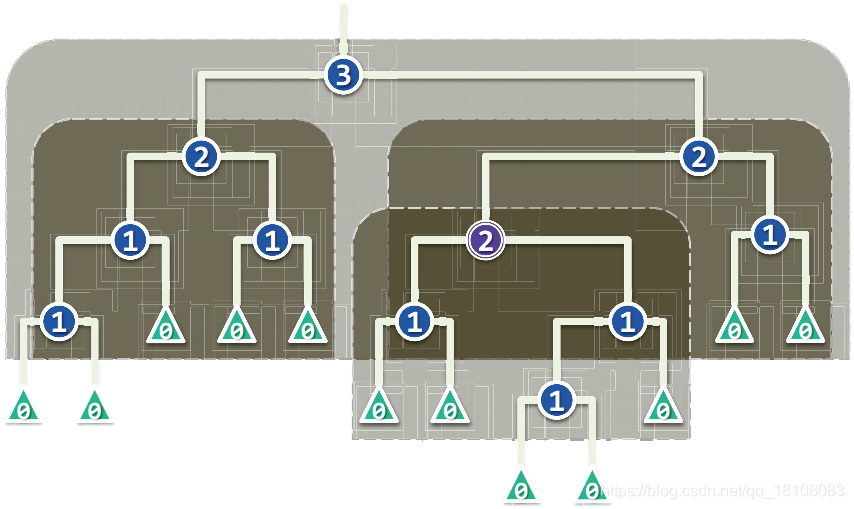
空节点路径长度(nurl path length)
:记作npl(x),若x为外部节点,则约定 npl(x) = npl (null) =0,反之若x为内部节点,则npl (x)可递归地定义为:
npl(x) =1 + min(npl(lc(x)),npl(rc(x))
也就是说,节点x的npl取决于左右孩子npl值中的小者。
对照上图不难验证:
npl(x)既等于x到外部节点的最近距(该指标由此得名) ,同时也等于以x为根的最大满子树(图中矩形框)的高度
。
结构上的约束:
左式堆是处处满足“左倾性”的二叉堆,即任一内部节点x都满足:
npl(lc(x))>=npl(rc(x))
也就是说,就npl指标而言,任一内部节点的左孩子都不小于其右孩子,所以左式堆中每个节点的npl值都仅取决于其右孩子。
最右侧通路:
从x出发沿右侧分支一直前行直至空节点,经过的通路称作其最右侧通路(rightmost path)
,记作rPath(x),由“各节点npl值均决定与其右孩子”这一事实不难发现,每个节点的npl值,应恰好等于其最右侧通路的长度。
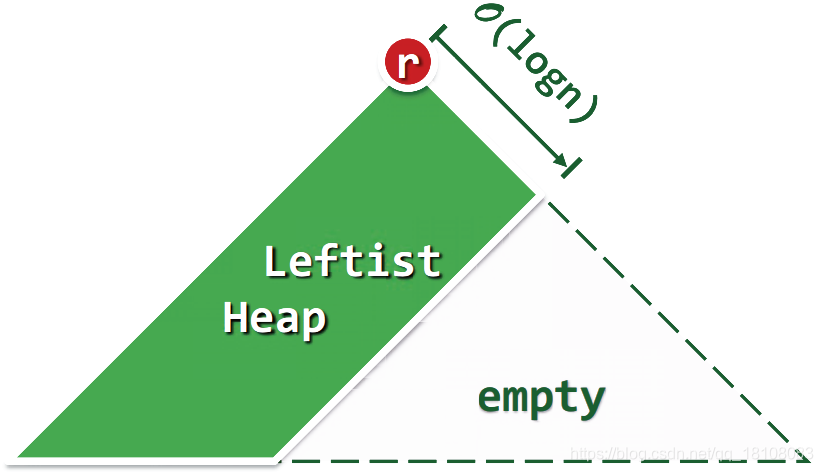
事实上,在包含n个节点的左式堆中,最右侧通路不会长于O(logn)(可由极限情况–满二叉树的节点数和高度之间的关系证明)
。最右侧通路的最大长度限制确定了合并操作的时间复杂度的上界。
三、左式堆的操作
(1) 合并
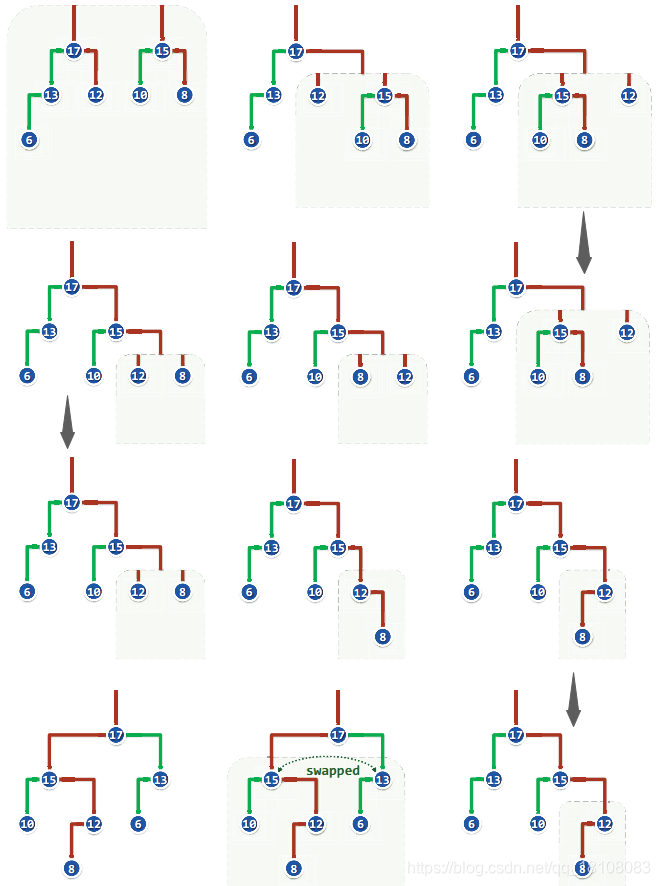
假设待合并的左式堆如下左图所示,分别以a和b为堆顶,且不失一般性地 a >= b。
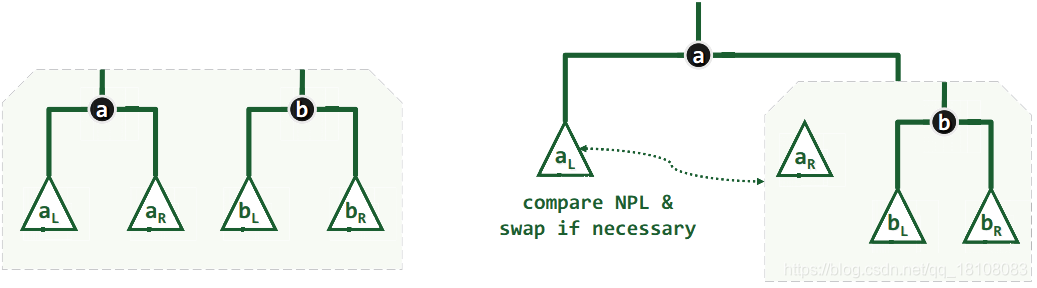
为合并两个堆,
可
递归
地将a的右子堆和堆b进行合并,然后将合并的子堆作为a的右子堆。为保证依然满足左倾性条件,最后还需要比较a左、右孩子的npl值,如有必要还要讲二者交换
,以保证左孩子的npl值不低于右孩子。
(a) 递归深入
对于两个需要合并的子堆,首先对堆顶进行优先级(关键码)的比较,把大者a作为左侧,小者b放在右侧(这样合并成的子堆才能作为a的孩子,因为a最大),大者的右子堆ar和右侧的堆b进行合并(过程和前述过程一样),合成的新堆作为a的右子堆,如此迭代向下,直至一侧堆为空。
(b) 递归返回
当(a)步骤结束后,在结构上两个堆已经合并完成,但为了保证左倾性依然处处满足,在沿左侧链逐级递归返回的过程中,还需及时比较各对左、右兄弟的npl值,如有必要还应令其交换位置。
复杂度分析: 递归只可能发生于两个待合并推的最右侧通路上。若待合并堆的规模分别为n和m,则其两条量右侧通路的长度则不会超过O(logn)和O(logm),因此合并算法的总体运行时间应不超过:
O(logn) +O(logm) = O(log(max(n, m)))
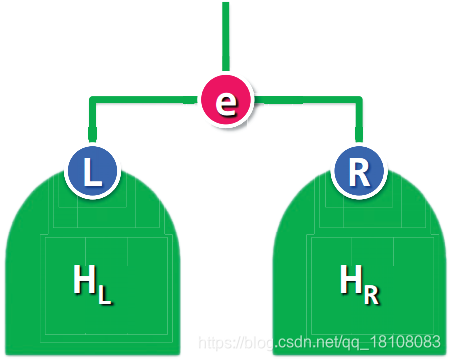
(2) 删除(基于合并)
在摘除e之后, 左右子堆即可被视作为两个彼此独立的将合井的堆,于是,只需通过合并操作将它们合并起来,则其效果完全等间于一次常规的删除操作。
复杂度分析:
时间成本主要是对合并操作的调用,总体不超过O(logn)。
(3) 插入(基于合并)
拟将元素e插入堆中,只要将x也视作仅含单个节点的堆,则通过合并操作将两个堆合并即可,其效果完全等同于完成了一次词条插入操作。

复杂度分析:
时间成本主要是对合并操作的调用,总体不超过O(logn)。
四、左式堆的实现
由于左式堆已经不满足结构性,所以不能使用向量作为底层容器,故采用二叉树的这种灵活的数据结构,所以左式堆类PQ_LeftHeap由二叉树类binTree和优先级队列PQ多重继承得到。
| 操作 | 功能 | 对象 |
| PQ_LeftHeap() | 默认构造函数 | 左式堆 |
| PQ_LeftHeap(T* E, int n) | 构造函数,由数组构造 | 左式堆 |
| insert(T e) | 按照比较器确定的优先级次序插入元素 | 左式堆 |
| getMax() | 取出优先级最高的元素 | 左式堆 |
| delMax() | 删除优先级最高的元素 | 左式堆 |
| merge(binNode<T>* a, binNode<T>* b) | 合并以a和b为根节点的左式堆 | 左式堆 |
(1) PQ_LeftHeap.h
#pragma once
#include"PQ.h"
#include"binTree.h"
#define lt(a,b) ((a)<(b)) //比较大小
/*左式堆是基于二叉树结构的*/
template<typename T> class PQ_LeftHeap :public PQ<T>, public binTree<T>
{
public:
//构造函数
PQ_LeftHeap() {}
PQ_LeftHeap(T* E, int n);
void insert(T e); //按照比较器确定的优先级次序插入元素
T getMax(); //取出优先级最高的元素
T delMax(); //删除优先级最高的元素
static binNode<T>* merge(binNode<T>* a, binNode<T>* b); //合并以a和b为根节点的左式堆
};
template<typename T> PQ_LeftHeap<T>::PQ_LeftHeap(T* E, int n)
{
for (int i = 0; i < n; i++) //直接插入
insert(E[i]);
}
template<typename T> binNode<T>* PQ_LeftHeap<T>::merge(binNode<T>* a, binNode<T>* b)
{
if (!a) return b; //递归基
if (!b) return a;
if (lt(a->data, b->data)) //保证左节点大
swap(a, b);
a->rc = merge(a->rc, b); //将a的右子堆与b合并
a->rc->parent = a;
if (!a->lc || a->lc->nlp < a->rc->npl) //若a的左孩子不存在或者a的左子树的npl比右子树的小,则转换左右子树
swap(a->lc, a->rc);
a->npl = a->rc ? a->rc->npl + 1 : 1; //更新a的npl
return a; //返回合并后的堆顶
}
template<typename T> T PQ_LeftHeap<T>::delMax()
{
binNode<T>* lHeap = _root->lc; //左子堆
binNode<T>* rHeap = _root->rc; //右子堆
T e = _root->date;
delete _root;
_size--;
_root = merge(lHeap, rHeap); //原左右子堆合并
if (_root)
_root->parent = nullptr;
return e;
}
template<typename T> T PQ_LeftHeap<T>::getMax()
{
return _root->date;
}
template<typename T> void PQ_LeftHeap<T>::insert(T e)
{
binNode<T>* v = new binNode<T>(e); //为e创建一个二叉树节点
_root = merge(_root,v); //通过合并完成插入
_root->parent = nullptr;
_size++;
}