一、选择题
1、二分搜索算法是利用（ A ）实现的算法。
A、分治策略 B、动态规划法 C、贪心法 D、回溯法
2、下列不是动态规划算法基本步骤的是（ A ）。
A、找出最优解的性质 B、构造最优解 C、算出最优解 D、定义最优解
3、衡量一个算法好坏的标准是（ D ）。
A 运行速度快 B 占用空间少 C 时间复杂度低 D B和C
4．实现棋盘覆盖算法利用的算法是（ A ）。
A、分治法 B、动态规划法 C、贪心法 D、回溯法
5.下面是贪心算法的基本要素的是（ C ）。
A、重叠子问题 B、构造最优解 C、贪心选择性质 D、定义最优解
6. （ D ）是贪心算法与动态规划算法的共同点。
A、重叠子问题 B、构造最优解 C、贪心选择性质 D、最优子结构性质
7. 矩阵连乘问题的算法可由（ B ）设计实现。
A、分支界限算法 B、动态规划算法 C、贪心算法 D、回溯算法
8、使用分治法求解不需要满足的条件是（A ）。
A 子问题必须是一样的 B 子问题不能够重复
C 子问题的解可以合并 D 原问题和子问题使用相同的方法解
9．下列是动态规划算法基本要素的是（ D ）。
A、定义最优解 B、构造最优解 C、算出最优解 D、子问题重叠性质
10．下列算法中通常以自底向下的方式求解最优解的是（ B ）。
A、分治法 B、动态规划法 C、贪心法 D、回溯法
11．贪心算法与动态规划算法的主要区别是（ B ）。
A、最优子结构 B、贪心选择性质 C、构造最优解 D、定义最优解
12. 一个问题可用动态规划算法或贪心算法求解的关键特征是问题的（ B ）。
A、重叠子问题 B、最优子结构性质 C、贪心选择性质 D、定义最优解
二、 填空题
1.算法的复杂性有 时间 复杂性和 空间 复杂性之分。
2、程序是 算法 用某种程序设计语言的具体实现。
3、算法的“确定性”指的是组成算法的每条 指令 是清晰的，无歧义的。
4.矩阵连乘问题的算法可由 动态规划 设计实现。
5、算法是指解决问题的 一种方法 或 一个过程 。
6、从分治法的一般设计模式可以看出，用它设计出的程序一般使用 递归 机制 。
7、计算一个算法时间复杂度通常可以计算 循环次数 、 基本操作的频率 或计算步。
8、动态规划算法的基本思想是将待求解问题分解成若干 子问题 ，先求解 子问题 ，然后从这些 子问题 的解得到原问题的解。
9.算法是由若干条指令组成的有穷序列，且要满足输入、 输出 、确定性和 有限性 四条性质。
10.任何可用计算机求解的问题所需的时间都与其 规模 有关。
11. 写出下列f(n)的渐进性态：
1) f(n)=C，为常数：f(n)= O( 1 )。 2) f(n)= 3n+2：f(n)= O( n )。
3) f(n)= 6×2n+n：f(n)= O( 2n )。 4) f(n)= nlog n：f(n)= O( nlog n )。
12. 按照渐近阶从低到高的顺序排列以下表达式：4n2，logn，3n，20n，2，n2/3。又n!应该排在哪一位？
2，logn，n2/3，20n，4n2，3n，n！。
三、时间复杂度分析（写出分析过程）
1.汉诺塔问题的时间复杂度。
解：
汉诺塔问题的时间复杂性是完成ｎ个圆盘移动所移动的次数。设移动总次数为Ｔ(ｎ)，由于原问题分成了三个子问题：两个移动ｎ-1个圆盘的问题和一个移动一个圆盘的过程。两个移动ｎ-1个圆盘的问题采用递归调用，花时间Ｔ(ｎ-1)，移动一个圆盘花一个单位时间。所以的递归方程如下：
直接推导可得
2. 冒泡排序算法的基本运算如下：
for i ←1 to n-1 do
for j ←1 to n-i do
if a[j]<a[j+1] then
交换a[j]、a[j+1]；
分析该算法的时间复杂性。
解：排序算法的基本运算步为元素比较，冒泡排序算法的时间复杂性就是求比较次数与n的关系。
- 设比较一次花时间1
- 内循环次数为：n-i次,（i=1,…n），花时间为：
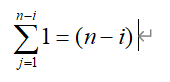
- 外循环次数为：n-1，花时间为：
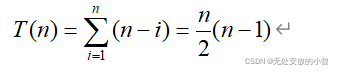
3． 递归求取最大和最小元素算法 MAXMIN的时间复杂性。
解：
设算法的元素比较次数为T(n)，mid将数组分成大小为
的两部分，递归调用原过程分别在两部分找max1、min1和max2、min2，分别花时间为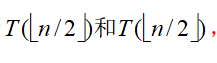
，比较max1、max2和min1、min2找出max、min所花时间为2。因此递归方程为：
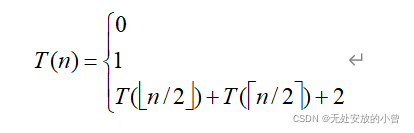
当n是2的幂时，即对于某个正整数k，n=2k，有
T(n)=2T(n/2)+2
＝2(2T(n/4)+2)+2
=4T(n/4)+4+2
……
＝2k-1+2k-2
＝3n/2-2
四、算法设计
1.有9件产品，其中一个不合格，不合格的产品比合格产品轻，现有一个天平，请设计算法用最少比较次数找到不合格产品。
答：本题使用分治法。算法设计步骤如下：
（1）将9件产品分成3组，每组3件产品。
（2）用天平称量其中任意两组，有两种情况：
第一种情况是天平上其中一组重量轻，则重量轻的一组产品转步骤（3）；
第二种情况是天平上的两组重量相等，则剩下的第三组转步骤（3）。
（3）将步骤（2）转来这组的3件产品，分开成3组，每组一件产品，用天平称量其中任意两件产品，有两种情况：
第一种：天平中有一件产品轻，则这件产品为不合格产品，算法结束。
第二种：天平中两件产品重量相等，则第三件产品为不合格产品，算法结束。
使用这样的分治法，可以在两次称量后得出结论，用的比较次数最少。
评分标准：设计出算法给5分，算法时间效率好给5分。