博客

广度优先搜索类似于树的按层次遍历的过程

遍历过程分析

1. 从图中某个顶点v出发，访问v。
2. 依次访问v的各个未曾访问过的邻接点。
3. 分别从这些邻接点出发依次访问它们的邻接点，并使“先访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。重复步骤（3），直至图中所有已经被访问的顶点的邻接点都被访问到。

如图：

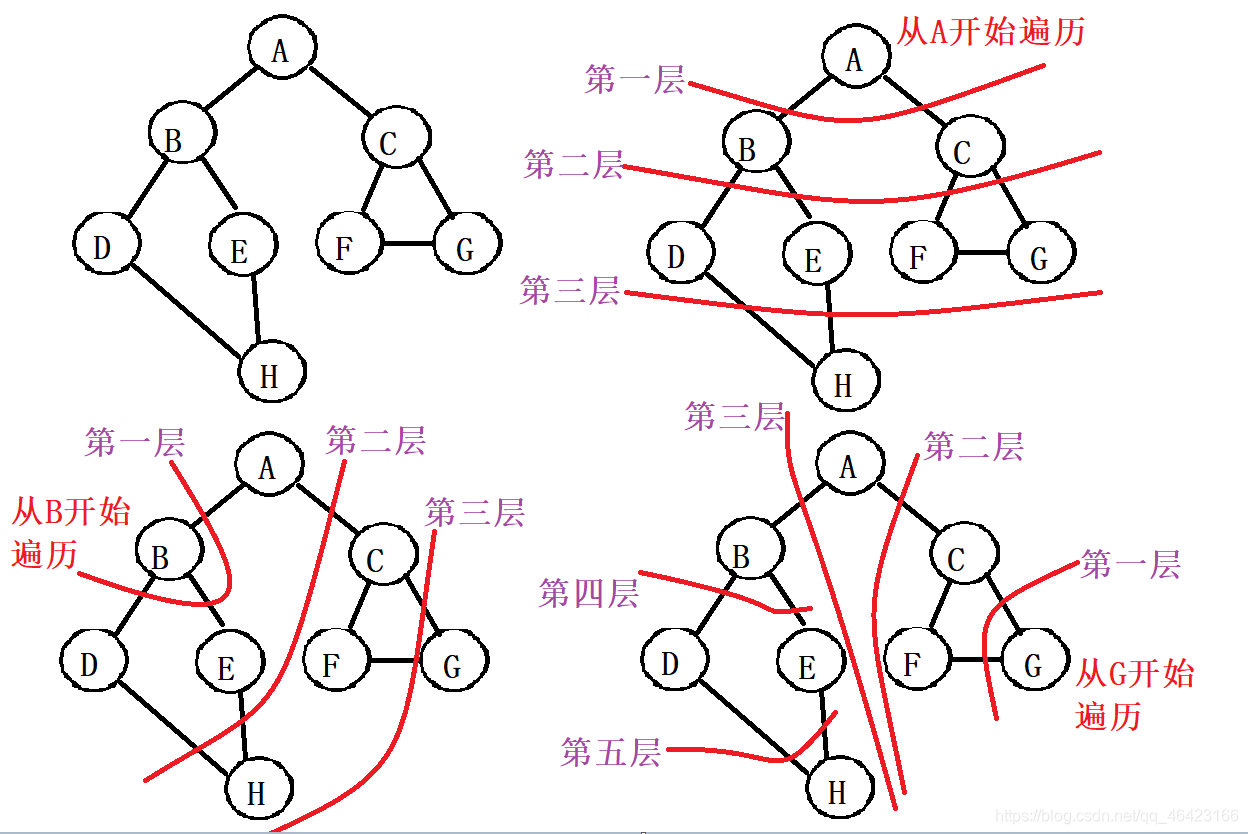
• 从A开始则为A-BC-DEFG-H
• 从B开始则为B-ADE-CFH-G
• 从G开始则为G-CF-A-B-DE-H（具体实现过程每层显示先后是按照输入先后，以具体输出为准，这是大致过程）

算法步骤

1. 从图中某个顶点v出发，访问v,并置visited[v]的值为0，然后将v进队。
2. 只要队列不为空，则重复下述操作

• 
  队头顶点u出队
  
• 
  依次检查u的所有邻接点w，如果visited[w]的值为0，则访问w，并置visited[w]的值为1，然后将w进队。
  

主要代码部分

int visited[100] = { 0 };
void BFS(AMgroup &A, int v)
{
	cout << A.VTchart[v];
	visited[v] = 1;             //将遍历点visited设为1
	List *Q = Init();
	Q = Enter(Q, v);            //入队
	while (Q->front != Q->rear)
	{
		int a = Delete(*Q);          //出队
		for (int i = 0; i < A.point; i++)
		{
			if (A.AMchart[a][i] != MaxInt&&visited[i] == 0)          //a，i两点连通，且i点并未遍历
			{
				cout << A.VTchart[i];
				visited[i] = 1;            //将i的visited设为1
				Q = Enter(Q, i);           //将i入队
			}
		}
	}
}

全部代码

#include<iostream>
using namespace std;

#define MaxSize 20
#define pointMax 100
#define MaxInt 32767


struct AMgroup
{
	char VTchart[pointMax];                  //顶点表
	int AMchart[pointMax][pointMax];         //邻接矩阵
	int point, vert;                         //点，边
};

int AMlocate(AMgroup A, char x)
{
	for (int i = 0; i < A.point; i++)       //依次输入点的信息
	{
		if (A.VTchart[i] == x)
		{
			return i;
			break;
		}
	}
}

void CreatAM(AMgroup &A)
{
	cout << "输入邻接矩阵顶点数：";                     //第一步
	cin >> A.point;
	cout << "输入邻接矩阵边数：";
	cin >> A.vert;
	getchar();

	char a[100];
	cout << "输入点的信息：";                          //第二步
	gets_s(a);
	for (int i = 0; i < A.point; i++)               //依次输入点的信息
	{
		A.VTchart[i] = a[i];
	}
	for (int i = 0; i < A.point; i++)              //初始换邻接矩阵，边的权值均设为最大           //第三步
	{
		for (int j = 0; j < A.point; j++)
		{
			A.AMchart[i][j] = MaxInt;
		}
	}

	cout << endl;
	char v1, v2; int len;
	for (int i = 1; i <= A.vert; i++)             //构造邻接矩阵
	{
		cout << "输入第" << i << "条边的两个顶点以及权值：";            //第四步
		cin >> v1 >> v2 >> len;
		int m, n;
		m = AMlocate(A, v1);
		n = AMlocate(A, v2);
		A.AMchart[m][n] = A.AMchart[n][m] = len;
	}
}

//队列部分
struct Node
{
	int data;         //数据域
	Node *next;       //下一个
};
struct List
{
	Node *front;      //尾
	Node *rear;       //头
};


List *Init()
{
	List *S = new List;
	S->front = S->rear = new Node;
	S->front->next = NULL;
	return S;
}

List *Enter(List *S ,int a)
{
	Node *P = new Node;
	P->data = a;
	P->next = NULL;
	S->rear->next = P;
	S->rear = P;
	return S;
}

int Delete(List &S)
{
	int a;
	if (S.front != S.rear)
	{
		a = S.front->next->data;
		S.front = S.front->next;
		return a;
	}
}

int visited[100] = { 0 };
void BFS(AMgroup &A, int v)
{
	cout << A.VTchart[v];
	visited[v] = 1;             //将遍历点visited设为1
	List *Q = Init();
	Q = Enter(Q, v);            //入队
	while (Q->front != Q->rear)
	{
		int a = Delete(*Q);          //出队
		for (int i = 0; i < A.point; i++)
		{
			if (A.AMchart[a][i] != MaxInt&&visited[i] == 0)          //a，i两点连通，且i点并未遍历
			{
				cout << A.VTchart[i];
				visited[i] = 1;            //将i的visited设为1
				Q = Enter(Q, i);           //将i入队
			}
		}
	}
}

int main()
{
	AMgroup *A = new AMgroup;
	CreatAM(*A);
	int a;
	cout << "\n从第几个点开始遍历：";
	cin >> a;
	BFS(*A, a);
	system("pause");
}