Java常见算法(一)

文章目录

一、链表反转

1.迭代法

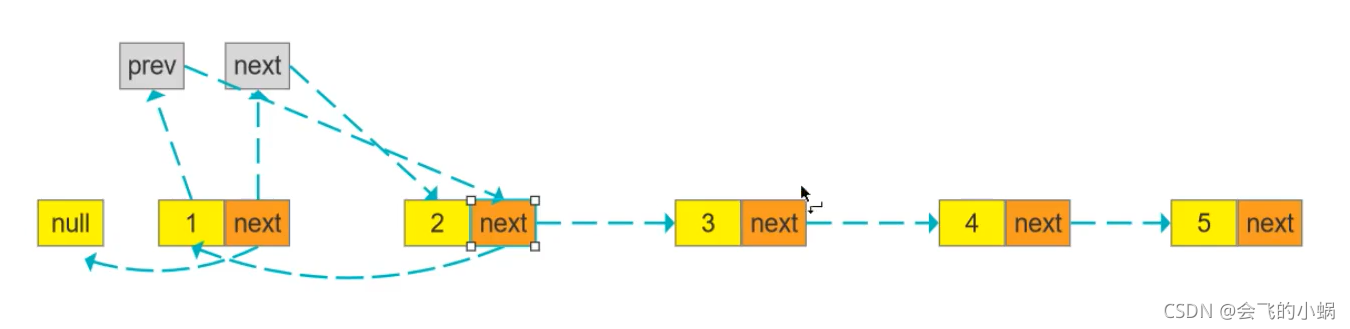
在这里插入图片描述

    //链表反转：1.迭代法
     private static LinkNode  getFZ0(LinkNode linkNode){
        //前一个
        LinkNode prev=null;//前一个节点
        LinkNode next;//下个节点
        LinkNode curr=linkNode;//当前的这个
        while (curr!=null){
            next=curr.next;//下个节点
            curr.next=prev;//把当前这个的下个节点指向前一个
            prev=curr;//对于后面的来说，前一个其实就是这个
            curr=next;//为了迭代，需要把本个循环里的主体换成下一个
        }
        //返回最后那个节点
        return prev;
     }
}

2.递归法

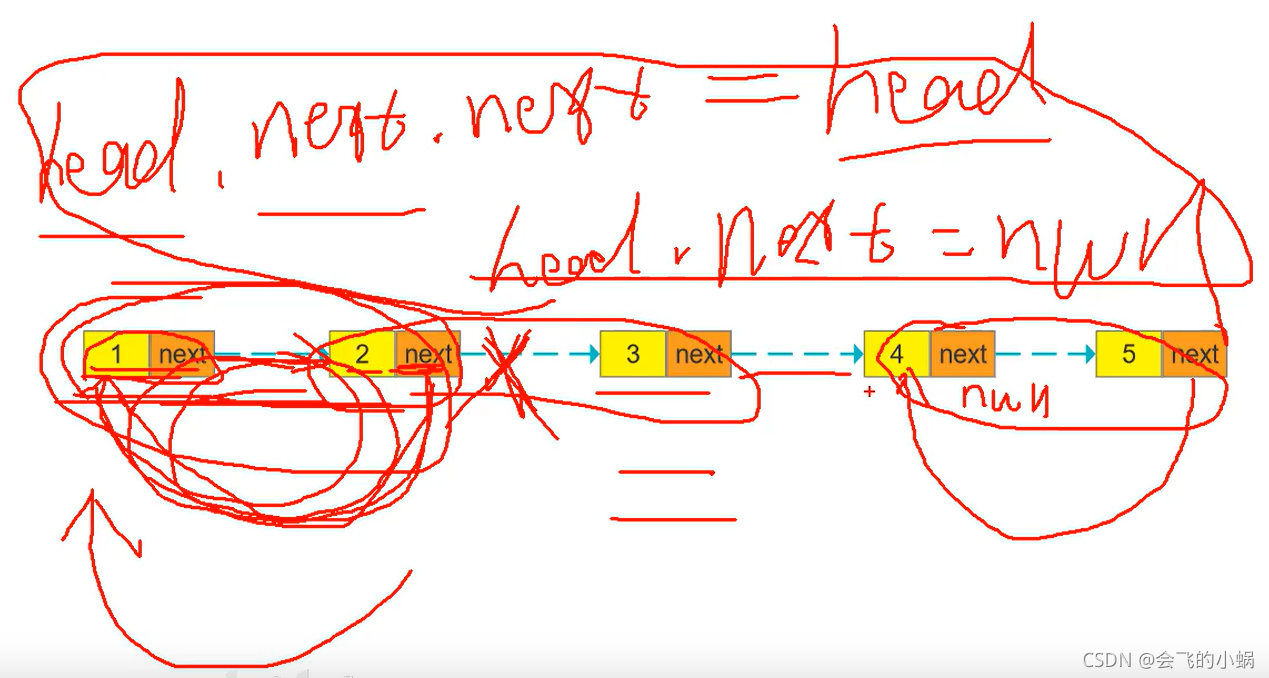
在这里插入图片描述

     //链表反转：2.递归
     private static LinkNode  getFZ1(LinkNode linkNode){
       	//无需反转的情况
         if(linkNode==null||linkNode.next==null){
             return linkNode;
         }
          //为了使用递归，我们需要找到最后一个节点，然后从最后一个节点来开始
         LinkNode newlinkNode = getFZ1(linkNode.next);// 一次一次的递归，直到找到最后一个节点
         linkNode.next.next=linkNode;//递归处理的话，下一个的下一个 是自己，这样的话就把指针的方向180度转换了
         linkNode.next=null; //把两个里面的下一个制成null
         return newlinkNode;
     }

源码实验 ( 需要以打断点的形式来看！！！)：

package com.example.rabbitmq;

import com.baomidou.mybatisplus.core.conditions.query.QueryWrapper;
import com.baomidou.mybatisplus.core.metadata.IPage;
import com.baomidou.mybatisplus.extension.plugins.pagination.Page;
import com.example.rabbitmq.mapper.UserMapper;
import com.example.rabbitmq.pojo.User;
import org.junit.jupiter.api.Test;
import org.springframework.beans.factory.annotation.Autowired;
import org.springframework.boot.test.context.SpringBootTest;

import java.math.BigDecimal;
import java.util.Map;
import java.util.UUID;

@SpringBootTest
class SuanfaApplicationTests {

    //模拟链表
    static class LinkNode{
        private Integer v;
        private LinkNode next;
        public LinkNode(Integer v, LinkNode next) {
            this.v = v;
            this.next = next;
        }
    }

    //链表反转：1.迭代法
     private static LinkNode  getFZ0(LinkNode linkNode){
        //前一个
        LinkNode prev=null;//前一个节点
        LinkNode next;//下个节点
        LinkNode curr=linkNode;//当前的这个
        while (curr!=null){
            next=curr.next;//下个节点
            curr.next=prev;//把当前这个的下个节点指向前一个
            prev=curr;//对于后面的来说，前一个其实就是这个
            curr=next;//为了迭代，需要把本个循环里的主体换成下一个
        }
        //返回最后那个节点
        return prev;
     }

     //链表反转：2.递归
     private static LinkNode  getFZ1(LinkNode linkNode){
        //为了使用递归，我们需要从最后一个节点来开始
         if(linkNode==null||linkNode.next==null){
             return linkNode;
         }
         LinkNode newlinkNode = getFZ1(linkNode.next);// 一次一次的递归，直到找到最后一个节点
         linkNode.next.next=linkNode;//递归处理的话，下一个的下一个 是自己，这样的话就把指针的方向180度转换了
         linkNode.next=null; //把两个里面的下一个制成null
         return newlinkNode;
     }

    @Test
    public void sf0(){
        LinkNode linkNode5 = new LinkNode(5, null);
        LinkNode linkNode4 = new LinkNode(4, linkNode5);
        LinkNode linkNode3 = new LinkNode(3, linkNode4);
        LinkNode linkNode2 = new LinkNode(2, linkNode3);
        LinkNode linkNode1 = new LinkNode(1, linkNode2);
      
          //迭代法处理链表反转
//        LinkNode fz0 = getFZ0(linkNode1);
//        System.out.println(fz0.toString());

        //递归
        LinkNode fz1 = getFZ1(linkNode1);
        System.out.println(fz1.toString());

    }

}

断点查看到的反转结果：

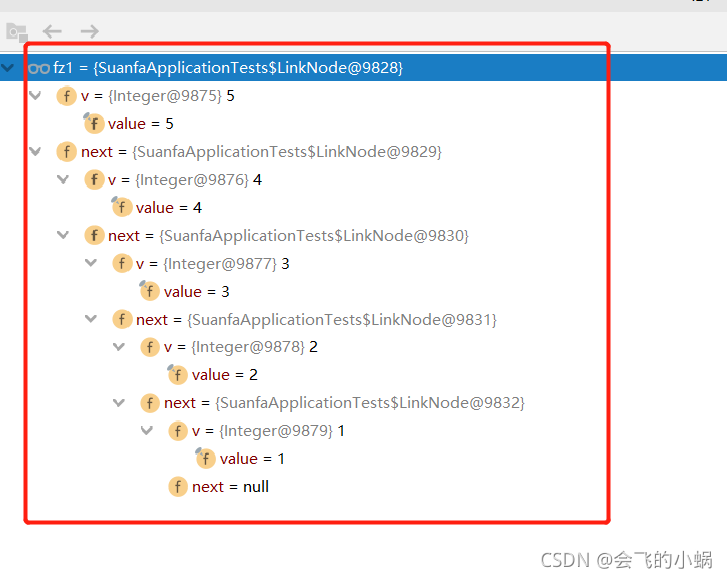
在这里插入图片描述

二、统计 n 以内的素数个数

素数：只能被1或者自身整除的自然数，0、1除外

1.暴力算法（直接循环无脑开找）

 //1. 暴力算法
    public static String getCount(int n){
        //计数器
        int c=0;
        //遍历
        for (int i = 2; i < n; i++) {
            c+=checkSS_YH(i)?1:0;
        }
        return n+"以内的素数个数为："+c;
    }

    //判断传入的是否为素数
    private static boolean checkSS(int x){
        for (int i = 2; i <x ; i++) {
            //判断是否可以被整除
            if(x%i==0){
                return false;
            }
        }
        return true;
    }

2.埃筛法（重点）

利用合数的概念（非素数），素数 * n 必然是合数，因此何以从2开始遍历，将会所有的合数做上标记.

/**
     * 利用合数的概念（非素数），素数 * n 必然是合数，因此何以从2开始遍历，将会所有的合数做上标记
     * 将合数标记为true,j=i*i 从 2*i 优化而来
     * @param n
     * @return
     */
    public static String eratosthenes(int n){
         boolean[] isPrime=new boolean[n];
         int ans=0;
         for (int i=2;i<n;i++){
             if(!isPrime[i]){
                 ans+=1;
                 for (int j=i*i;j<n;j+=i){
                     isPrime[j]=true;
                 }
             }
         }
        return n+"以内的素数个数为："+ans;
    }

源码实验：

package com.example.rabbitmq;

import org.junit.jupiter.api.Test;
import org.springframework.boot.test.context.SpringBootTest;

@SpringBootTest
/**
 * 统计 n 以内 的 素数个数
 * （素数：只能被1或者更自身整除的自然数，0、1除外）
 */
class SuanfaApplicationTests2 {


    //1. 暴力算法
    public static String getCount(int n){
        //计数器
        int c=0;
        //遍历
        for (int i = 2; i < n; i++) {
            c+=checkSS(i)?1:0;
        }
        return n+"以内的素数个数为："+c;
    }

    //判断传入的是否为素数
    private static boolean checkSS(int x){
        for (int i = 2; i <x ; i++) {
            //判断是否可以被整除
            if(x%i==0){
                return false;
            }
        }
        return true;
    }

    //2.埃筛法（重点）

    /**
     * 利用合数的概念（非素数），素数 * n 必然是合数，因此何以从2开始遍历，将会所有的合数做上标记
     * 将合数标记为true,j=i*i 从 2*i 优化而来，
     *
     * @param n
     * @return
     */
    public static String eratosthenes(int n){
         boolean[] isPrime=new boolean[n];
         int ans=0;
         for (int i=2;i<n;i++){
             if(!isPrime[i]){
                 ans+=1;
                 for (int j=i*i;j<n;j+=i){
                     isPrime[j]=true;
                 }
             }
         }
        return n+"以内的素数个数为："+ans;
    }

    @Test
    public void sf0(){
        System.out.println(getCount(100));

        System.out.println(eratosthenes(100));

    }

}

返回结果：

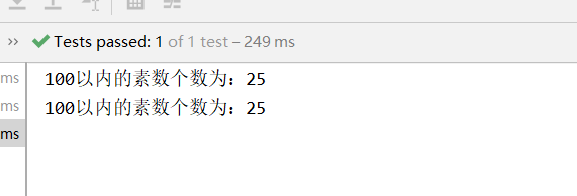
在这里插入图片描述

三、删除排序数组中的重复项

描述：一个有序数组nums ，原地删除重复出现的元素，使每个元素只出现一次，返回删除后的数组新长度

要求：不能使用额外的数组空间，必须在原地修改输入数组并在使用O(1)额外空间的条件下完成。

双指针算法

//双指针算法
    public static String getCountSZZ(int[] nums){
        int i=0;//定义一个慢指针
        int length = nums.length;
        for (int j=1;j<length;j++){
            if (nums[i]!=nums[j]){
                i++;
                nums[i]=nums[j];
            }
        }
        return "去重后数组长度为："+i;
    }

源码实验：

package com.example.rabbitmq;

import org.junit.jupiter.api.Test;
import org.springframework.boot.test.context.SpringBootTest;

@SpringBootTest
/**
 *删除排序数组中的重复项
 *一个有序数组nums ，原地删除重复出现的元素，使每个元素只出现一次，返回删除后的数组新长度。
 *要求： 不能使用额外的数组空间，必须在原地修改输入数组并在使用O(1)额外空间的条件下完成。
 */
class SuanfaApplicationTests3 {

    //双指针算法
    public static String getCountSZZ(int[] nums){
        int i=0;//定义一个慢指针
        int length = nums.length;
        for (int j=1;j<length;j++){
            if (nums[i]!=nums[j]){
                i++;
                nums[i]=nums[j];
            }
        }
        return "去重后数组长度为："+i;
    }

    @Test
    public void sf0(){
        //定义一个数组
        int[] intArrays=new int[]{1,2,3,3,6,6,8};
        String countSZZ = getCountSZZ(intArrays);
        System.out.println(countSZZ);
    }

}

返回结果：

在这里插入图片描述

四、寻找数组的中心下标

给定一个数组nums, 请编写一个能够返回数组“中心下标”的方法。

中心下标是数组的一个下标，其左侧相加的和等于其右侧相加的和。

如果数组不存在中心下标，需要进行告知，如果存在多个中心下标，返回最左边的那一个。

注意：中心下标可能出现在数组的两端。

解法之一（思路）：中心数组下标的左侧的2倍必为数组总和减去中心下标！

数学逻辑： 2*(中心下标左侧和)+中心下标=总和

    // 数组的中心下标
    public static String getCenterPort(int[] nums){
        //先算出数组的总和
        int sumAll = Arrays.stream(nums).sum();
        //数组下标左侧的和
        int sunLeft=0;
        for (int i=0;i<nums.length;i++){
           sunLeft+=nums[i];
           //(i+1<nums.length) 这个条件要注意一下，别搞成数组越界了
           if((i+1<nums.length)&&(sumAll-sunLeft-nums[i+1])==sunLeft){
               return "数组中心下标为"+(i+1);
           }
        }
        return "没找到数组中心下标!";
    }

源码实验：

package com.example.rabbitmq;

import org.junit.jupiter.api.Test;
import org.springframework.boot.test.context.SpringBootTest;

import java.util.Arrays;

@SpringBootTest
/**
寻找数组的中心下标：
 给定一个数组nums, 请编写一个能够返回数组“中心下标”的方法。

 中心下标时数组的一个下标，其左侧相加的和等于其右侧相加的和。
 如果数组不存在中心下标，返回-1，如果存在多个中心下标，返回最左边的那一个。
 注意：中心下标可能出现在数组的两端。

 解法之一（思路）：中心数组下标的左侧的2倍必为 数组总和减去中心下标！
 */
class SuanfaApplicationTests4 {

    // 数组的中心下标
    public static String getCenterPort(int[] nums){
        //先算出数组的总和
        int sumAll = Arrays.stream(nums).sum();
        //数组下标左侧的和
        int sunLeft=0;
        for (int i=0;i<nums.length;i++){
           sunLeft+=nums[i];
           //(i+1<nums.length) 这个条件要注意一下，别搞成数组越界了
           if((i+1<nums.length)&&(sumAll-sunLeft-nums[i+1])==sunLeft){
               return "数组中心下标为"+(i+1);
           }
        }
        return "没找到数组中心下标!";
    }

    @Test
    public void sf0(){
        //定义一个数组
        int[] intArrays=new int[]{1,7,3,6,5,6};
        String countSZZ = getCenterPort(intArrays);
        System.out.println(countSZZ);
    }

}

结果：

在这里插入图片描述

五、求X的平方根

要求：在不适用sqrt(x)函数的情况下，得到x 的平方根的整数部分

重点考察：二分法、牛顿迭代

1、二分查找 ,时间复杂度 logN

public static String binarySearch(int x){
        //定义一个返回值
        int index=-1;
        //左指针
        int l=0;
        //右指针
        int r=x;
        while (l<=r){
            //假如有平方根，则为这个
            int mid=l+(r-l)/2;
            //如果这个指针满足这个条件（证明x 的平方分还没到,还要比这个mid大，L的指针就向右移动）
            if(mid*mid<=x){
                index=mid;
                l=mid+1;
            }else {
                r=mid-1;
            }
        }
        return x+" 的平方根整数部分为："+ index;
    }

重点：假设的平方根公式为

左指针为 L ，右指针为 R

则：L+(R-L)/2

2、牛顿迭代

(抛物线理论的递归查找)，n的平方等于x , n等于 x/n : (n + x/n )/2

 //2.牛顿迭代 (抛物线理论的递归查找)，n的平方等于x , n等于 x/n  :  (x/n + n)/2
    public static int niudun(int x){
        //需要进行排除0
        if(x==0){
            return x;
        }
        return (int) sqrt(x,x);
    }
    private static double sqrt(double n,int x){
        //牛顿迭代的基本公式，记下！
        double mid=(n+x/n)/2;
        if(mid==n){
            return mid;
        }else {
            return sqrt(mid,x);
        }
    }

实验源码：

package com.example.rabbitmq;

import org.junit.jupiter.api.Test;
import org.springframework.boot.test.context.SpringBootTest;

import java.util.Arrays;

@SpringBootTest
/**
 X的平方根
在不适用sqrt(x)函数的情况下，得到x 的平方根的整数部分
重点考察：二分法、牛顿迭代
 */
class SuanfaApplicationTests5 {

    // 1.二分查找,时间复杂度 logN
    public static String binarySearch(int x){
        //定义一个返回值
        int index=-1;
        //左指针
        int l=0;
        //右指针
        int r=x;
        while (l<=r){
            //假如有平方根，则为这个
            int mid=l+(r-l)/2;
            //如果这个指针满足这个条件（证明x 的平方分还没到,还要比这个mid大，L的指针就向右移动）
            if(mid*mid<=x){
                index=mid;
                l=mid+1;
            }else {
                r=mid-1;
            }
        }
        return x+" 的平方根整数部分为："+ index;
    }

    //2.牛顿迭代 (抛物线理论的递归查找)，n的平方等于x , n等于 x/n  :  (x/n + n)/2
    public static int niudun(int x){
        //需要进行排除0
        if(x==0){
            return x;
        }
        return (int) sqrt(x,x);
    }
    private static double sqrt(double n,int x){
        //牛顿迭代的基本公式，记下！
        double mid=(n+x/n)/2;
        if(mid==n){
            return mid;
        }else {
            return sqrt(mid,x);
        }
    }

    @Test
    public void sf0(){
        int x=23;
        String s = binarySearch(x);
        System.out.println("二分查找："+s);

        int nd = niudun(x);
        System.out.println("牛顿迭代："+nd);
    }

}

结果：

在这里插入图片描述

六、整型数组nums ，在数组中找出由三个数字组成的最大乘积，并输出这个乘积

先不考率乘积越界的问题。

整点考察：线性扫描。

经过分析, 一共三种情况：全为正数、全为负数、有正有负数。

1、基于排序的算法

//1、基于排序的算法  时间复杂度主要有排序决定，为 NlogN
    public static int sort(int[] nums){
        Arrays.sort(nums);//对数组进行排序
        int n=nums.length;
        return Math.max(nums[0]*nums[1]*nums[n-1],nums[n-1]*nums[n-2]*nums[n-3]);
    }

2、线性扫描

 //2.线性扫描：基于上面的排序算法，我们知道了只要找出五个数即可：也就是 两个最小值，和三个最大值；
    public static int getMaxMin(int[] nums){
        //min1 最小的值， min2第二小的值
        int min1 = Integer.MAX_VALUE,min2=Integer.MAX_VALUE;
        //max1最大的值， max2第二大， max3第三大
        int max1=Integer.MIN_VALUE,max2=Integer.MIN_VALUE,max3=Integer.MIN_VALUE;
        for (int x : nums) {
            //先找两个最小的值
            if(x<min1){
                min2=min1;
                min1=x;
            }else if(x<min2){
                min2=x;
            }
            //找三个最大的值
            if(x>max1){
                max2=max1;
                max3=max2;
                max1=x;
            }else if(x>max2){
                max3=max2;
                max2=x;
            }else if(x>max3){
                max3=x;
            }
        }
        //其实也就是：Math.max(nums[0]*nums[1]*nums[n-1],nums[n-1]*nums[n-2]*nums[n-3]);
        return Math.max(min1*min2*max1,max1*max2*max3);
    }

实验源码：

package com.example.rabbitmq;

import com.sun.org.apache.regexp.internal.RE;
import org.junit.jupiter.api.Test;
import org.springframework.boot.test.context.SpringBootTest;

import java.util.Arrays;

@SpringBootTest
/**
    整型数组nums ， 在数组中找出由三个数字组成的最大乘积，并输出这个乘积。
  先不考率乘积越界的问题。
 整点考察：线性扫描。
 一共三种情况： 全为正数、全为负数、有正有负数
 */
class SuanfaApplicationTests6 {

    //1、基于排序的算法  时间复杂度主要有排序决定，为 NlogN
    public static int sort(int[] nums){
        Arrays.sort(nums);//对数组进行排序
        int n=nums.length;
        return Math.max(nums[0]*nums[1]*nums[n-1],nums[n-1]*nums[n-2]*nums[n-3]);
    }

    //2.线性扫描：基于上面的排序算法，我们知道了只要找出五个数即可：也就是 两个最小值，和三个最大值；
    public static int getMaxMin(int[] nums){
        //min1 最小的值， min2第二小的值
        int min1 = Integer.MAX_VALUE,min2=Integer.MAX_VALUE;
        //max1最大的值， max2第二大， max3第三大
        int max1=Integer.MIN_VALUE,max2=Integer.MIN_VALUE,max3=Integer.MIN_VALUE;
        for (int x : nums) {
            //先找两个最小的值
            if(x<min1){
                min2=min1;
                min1=x;
            }else if(x<min2){
                min2=x;
            }
            //找三个最大的值
            if(x>max1){
                max2=max1;
                max3=max2;
                max1=x;
            }else if(x>max2){
                max3=max2;
                max2=x;
            }else if(x>max3){
                max3=x;
            }
        }
        //其实也就是：Math.max(nums[0]*nums[1]*nums[n-1],nums[n-1]*nums[n-2]*nums[n-3]);
        return Math.max(min1*min2*max1,max1*max2*max3);
    }

    @Test
    public void sf0(){
        int[] nums=new int[]{2,3,1,6,-8,-9};
        int sort = sort(nums);
        int maxMin = getMaxMin(nums);

        System.out.println("基于排序的算法结果："+sort);
        System.out.println("基于线性扫描的算法结果："+maxMin);

    }

}

结果:

基于排序的算法结果：432
基于线性扫描的算法结果：432

原文链接：https://blog.csdn.net/YL3126/article/details/121155405

文章目录

一、链表反转

1.迭代法

2.递归法

二、统计 n 以内 的 素数个数

1.暴力算法（直接循环无脑开找）

2.埃筛法（重点）

三、删除排序数组中的重复项

双指针算法

四、寻找数组的中心下标

数学逻辑： 2*(中心下标左侧和)+中心下标=总和

五、 求X的平方根

1、二分查找 ,时间复杂度 logN

2、牛顿迭代

六、整型数组nums ， 在数组中找出由三个数字组成的最大乘积，并输出这个乘积

1、基于排序的算法

2、线性扫描

你可能也喜欢

二、统计 n 以内的素数个数

五、求X的平方根

六、整型数组nums ，在数组中找出由三个数字组成的最大乘积，并输出这个乘积