矩阵的条件数
(condition number)是数值分析和线性代数中的一个重要概念,它刻画了矩阵某方面的特性。
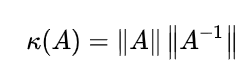
为矩阵 A 的条件数。结合上面提到的几何意义,条件数同时描述了矩阵A 对向量的拉伸能力和压缩能力,换句话说,令向量发生形变的能力。条件数越大,向量在变换后越可能变化得越多。
奇异值分解(SVD)
也是对矩阵进行分解,但是和特征分解不同,SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵,那么我们定义矩阵A的SVD为:
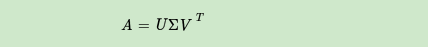
其中 U是一个 m * m 的矩阵,
Σ
\Sigma
Σ
是一个m * n的矩阵,除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值,V是一个n * n的矩阵。
U 和 V都是酉矩阵,即满足
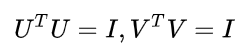
版权声明:本文为qq_40851561原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。