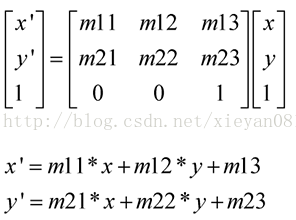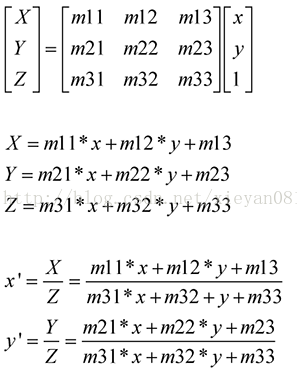仿射变换
1) 用途
旋转 (线性变换),平移 (向量加).缩放(线性变换),错切,反转
2) 方法
仿射变换是一种二维坐标到二维坐标之间的线性变换,它保持了二维图形的“平直性”(直线经过变换之后依然是直线)和“平行性”(二维图形之间的相对位置关系保持不变,平行线依然是平行线,且直线上点的位置顺序不变)。任意的仿射变换都能表示为乘以一个矩阵(线性变换),再加上一个向量 (平移) 的形式.
以上公式将点(x,y)映射到(x’,y’),在OpenCV中通过指定一个2×3矩阵实现此功能(公式中的m矩阵,是线性变换和平移的组合,m11,m12,m21,m22为线性变化参数,m13,m23为平移参数,其最后一行固定为0,0,1,因此,将3×3矩阵简化为2×3)
3) 举例
a) 以原点为中心旋转,2×3矩阵为:
[ cos(theta), -sin(theta), 0 ],
[ sin(theta), cos(theta), 0 ]
则
x’ = x * cos(theta) – sin(theta) * y
y’ = x * sin(theta) + cos(theta) * y
b) 平移,2×3矩阵为
[1,0,tx],
[0,1,ty]
则
x’ = x * 1 + y * 0 + tx = x + tx
y’ = x * 0 + y * 1 + ty = y + ty
4) 具体应用
在OpenCV中,仿射变换通过函数cvWrapAffine(src,dst,mat)实现,其中mat是2×3的仿射矩阵,该矩阵可以利用函数cvGetAffineTransform(srcTri,dstTri,mat)得到,其中mat是被该函数填充的仿射矩阵,srcTri和dstTri分别是由三个顶点定义的平行四边形(由于是平行四边形,只需要指定三个顶点即可确定),即:给出变换前的ABCD和变换后的A’B’C’D’

透视变换(投影变换)
1) 用途
将2D矩阵图像变换成3D的空间显示效果,全景拼接.
2) 方法
透视变换是将图片投影到一个新的视平面,也称作投影映射.它是二维(x,y)到三维(X,Y,Z),再到另一个二维(x’,y’)空间的映射.
相对于仿射变换,它提供了更大的灵活性,将一个四边形区域映射到另一个四边形区域(不一定是平行四边形).它不止是线性变换.但也是通过矩阵乘法实现的,使用的是一个3×3的矩阵,矩阵的前两行与仿射矩阵相同(m11,m12,m13,m21,m22,m23),也实现了线性变换和平移,第三行用于实现透视变换.
以上公式设变换之前的点是z值为1的点,它三维平面上的值是x,y,1,在二维平面上的投影是x,y,通过矩阵变换成三维中的点X,Y,Z,再通过除以三维中Z轴的值,转换成二维中的点x’,y’.
从以上公式可知,仿射变换是透视变换的一种特殊情况.它把二维转到三维,变换后,再转映射回之前的二维空间(而不是另一个二维空间).
3) 具体应用
在OpenCV中,透视变换通过函数cvWrapPerspective(src,dst,mat)实现, 与仿射变换不同的是,透视矩阵是一个3×3的矩阵,在计算矩阵时,可利用函数cvGetPerspectiveTransform(srcQuad,dstQuad,mat),由于不再是平行四边形,需要提供四边形的四个顶点

区别
仿射变换后平行四边形的各边仍操持平行,透视变换结果允许是梯形等四边形,所以仿射变换是透视变换的子集
实例:
1. 仿射变换
https://blog.csdn.net/augusdi/article/details/9022447
2. 透视变换
https://blog.csdn.net/Augusdi/article/details/9022197
转载自: