论文地址:O(ND)差分算法及其变体
寻找两个序列a和B的最长公共子序列以及将a转换为B的最短编辑脚本的问题一直被认为是对偶问题。本文证明了它们等价于在编辑图中寻找最短/最长路径。利用这个观点,我们发展了一个简单的O(N D)时空算法,其中N是a和B的长度之和,D是A和B的最小编辑脚本。当差异很小(序列相似)时,该算法性能良好,因此在典型应用中速度很快。该算法显示为
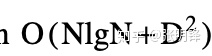
基本随机模型下的期望时间性能。算法的改进只需要yo(N)空间,后缀树的使用导致
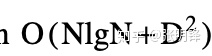
时间变化。
确定两个符号序列之间的差异的问题已经被广泛研究。
该问题的算法有很多应用,包括拼写纠正系统、文件比较工具和形式化的遗传进化研究,问题陈述是
查找最长的公共子序列,或等效地查找将一个序列转换为另一个序列的符号删除和插入的最小“脚本”。最早的算法之一是Wagner&Fischer和用
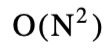
时间和空间来解决一个泛化问题,他们称之为串对串修正问题。稍后
Hirschberg的求精只使用线性空间提供最长的公共子序列。当算法超过任意字母表时,使用“相等-不相等”比较,并根据它们的大小来描述输入,已经表明
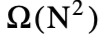
时间是必要的。“四个俄罗斯人”的方法使得任意和有限字母的
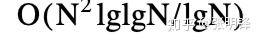
和
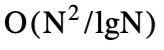
时间算法分别稍好一些。这个
使用其他比较格式的快速算法的存在仍然是开放的。实际上,对于使用“小于等于大于”比较的算法,
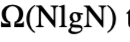
时间是已知的最佳下限.
最近的工作改进了基本的时间
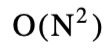
任意字母表算法,对其他问题大小参数敏感。设输出参数L为最长公共子序列的长度,并设对偶参数D=2(N-L)是最短编辑脚本的长度。(在整个介绍过程中,假设两个字符串的长度都是相同的N。)两个对输出敏感的最佳算法是由Hirschberg 使用了O(NL+NlgN)和O(DLlgN)时间。Hunt&Szymanski的一种算法需要O((R+N)lgN)时间,其中参数R是两个输入字符串匹配的有序位置对的总数。请注意仅就N而言,这些算法是Ω(N2)或更差。
在实际情况下,通常是参数D很小。程序员想知道他们是如何改变文本文件的。生物学家想知道一条DNA链是如何变异成另一条的。在这种情况下O(N D)时间算法优于Hirschberg算法,因为当D很小时,L是O(N)。此外,Hunt和Szymanski的方法是基于实践中R很小的假设。显然,必须注意R与输入或输出的大小没有相关性,并且在许多情况下可以是
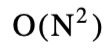
。例如,如果一个文件中有10%的行是空的,并且比较该文件相对于自身,R大于.01N2。对于DNA分子来说,字母表的大小是4,这意味着当任意一个分子与自身或非常相似的分子进行比较时,R至少是
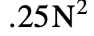
本文提出了一种O(ND)时间算法。我们的算法很简单,并且基于直观的编辑图形形式主义。与其他人不同的是,它采用了“贪婪”的设计范式,并揭示了“长”与“长”的关系将最常见的子序列问题转化为单源最短路径问题。另一个O(ND)算法在别处发表[16]。但是,它使用不同的设计范式,并且不共享以下特性。
该算法可以被改进为只使用线性空间,并且其预期的案例时间行为被证明是
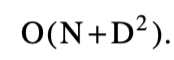
此外,该方法允许
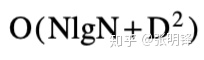
时间最坏情况变化。当D为o(N)时,这与以前的算法[8,16,20]相比是渐近的。
除了
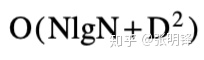
在最坏情况下,本文提出的算法是实用的.基本的O(ND)算法是UNIX diff程序新实现的基础。这个版本通常比基于Hunt和Szymanski的System 5实现快2到4倍算法。但是,当D较大时,有些情况下它们的算法更优(例如,对于完全不同,R=0,D=2N)。线性空间补给的速度大约是基本O(ND)的两倍
算法,但仍然具有竞争力,因为它可以执行超出其他算法范围的非常大的比较算法。例如,两个150万字节的序列在不到两分钟的时间内进行了比较(在VAX 785上运行4.2BSD UNIX),即使差异大于500。
编辑图形
设A=A 1 A 2. . . a N和B=b1 b2. . . b M分别是长度N和M的序列。的编辑图B在网格中的每个点上都有一个顶点(x,y),x∈[0,N]和y∈[0,M]。编辑图的顶点是连续的由水平、垂直和对角有向边连接形成有向无环图。水平边缘将每个顶点连接到其右邻域,即(x-1,y)—(x,y)表示x∈[1,N]和y∈[0,M]。垂直边缘连接每个
顶点到它下面的邻域,即(x,y-1)—(x,y)对于x∈[0,N]和y∈[1,M]。如果
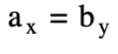
由然后是对角线
边连接顶点(x-1,y-1)到顶点(x,y)。x,y点 x=by称为匹配点。A和B之间的匹配点总数是Hunt&Szymanski算法的参数R。它也是编辑图中对角线边的数目,因为对角线边与匹配点一一对应。图1描述了序列A=abcabba和B=cbabac的编辑图。
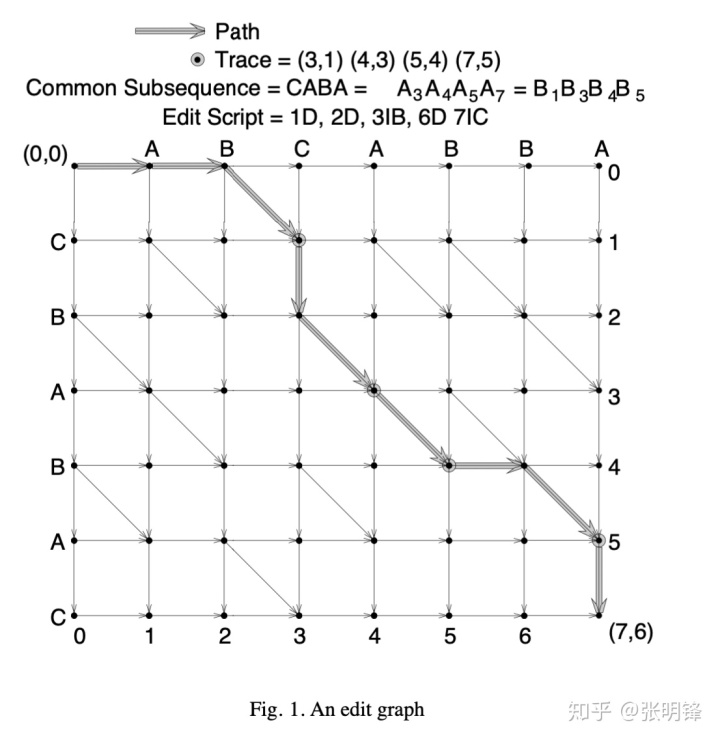
长度L的轨迹是L个匹配点(x1,y1)(x2,y2). . .(x L ,y L ),,使得xi < xi + 1和Yi < Yi+ 1为连续点(xi,yi)和(Xi+ 1,Yi+1),i〔1,L-1〕。每一个痕迹都与编辑图中从(0,0)到(N,M)的路径的对角线边。从开始到结束遍历路径时访问的匹配点序列很容易被验证为跟踪。注意,L是对应的路径。若要从轨迹构造路径,请采用与轨迹匹配点相对应的对角线顺序,并将连续的对角线与一系列水平和垂直边连接起来。 永远可以被实现为xi < xi + 1 和 yi < yi + 1。对于连续的匹配点。注意,有几个路径仅在它们的非对角边可以对应于给定的轨迹。图1说明了路径和跟踪之间的这种关系。
字符串的子序列是通过从给定字符串中删除零个或多个符号而获得的任何字符串。两个字符串A和B的com mon子序列是两者的子序列。每一个轨迹产生一个A和B的公共子序列,反之亦然。具体来说,一个x1一个x2。a x L=by1by2。。。由我是a和B的公共子序列,仅当(x1,y1)(x2,y2)。(x L,y L)是a和B的痕迹。
A和B的编辑脚本是一组将A转换为B的插入和删除命令。删除命令“xD”删除符号A x从A.插入命令”x I b1,b2。bt“插入符号 b1的序列。bt紧跟在x之后。脚本命令是指任何命令之前a内的符号位置已经完成了。必须将脚本中的命令集看作是同时执行的。这个脚本的长度是插入和删除的符号数。
每个跟踪都与编辑脚本唯一对应。设(x1,y1)(x2,y2)…(x L,y L)是一个痕迹。设y0=0,y L+1=M+1。关联的脚本由以下命令组成:x∈/{x1,x2。,x L},和“xkI byk+1。,对于k,byk+1−1”,这样yk+1<yk+1
. 脚本删除N-L个符号并插入M-L个符号。因此,对于长度L的每个跟踪,都有一个长度D=N+M-2L的对应脚本
一个trace,只需对a执行所有delete命令,观察结果是a和B的公共子序列,然后然后将子序列映射到其唯一的跟踪。请注意,反转insert命令的操作将提供一组将B映射到同一公共子序列的delete命令。
编辑图中的公共子序列、编辑脚本、跟踪和从(0,0)到(N,M)的路径都是同构形式。每个路径的边都有以下直接解释,即对应的com mon子序列和编辑脚本。每个以(x,y)结尾的对角线边都给出一个符号,即
子序列;每个水平边到点(x,y)对应于删除命令“x D”;以及从(x,y)到(x,z)的垂直边对应于insert命令,“x I by+1,…”。,bz“。因此,路径中垂直和水平边的数量是其相应脚本的长度,对角线边的数量是其对应子序列的长度,且边的总数为N+M-L。图1说明了这些观察结果。
寻找一个最长公共子序列(LCS)的问题相当于寻找一条从(0,0)到(N,M)具有最大对角线边数的路径。查找最短编辑脚本(SES)的问题相当于找到从(0,0)到(N,M)的路径,且非对角边的数目最小。这些是对偶问题,因为具有最大对角边数的路径具有最小非对角边数(D+2L=M+N)。考虑在每一个边缘增加一个权重或成本。给出对角线边权重0和非对角线边权重1。
LCS/SES问题等价于在加权编辑图中找到从(0,0)到(N,M)的最小代价路径,因而是单源最短路径问题的一个特例。
三。O((M+N)D)贪婪算法
查找最短编辑脚本的问题归结为查找从(0,0)到(N,M)的路径,而水平和垂直边的数目最少。设一个D-路径是从(0,0)开始的路径,该路径正好具有D个非对角线边缘。0-路径必须仅由对角边组成。通过一个简单的归纳,可以得出这样的结论:D-路径必须由一条(D-1)路径、一条非对角边和一个可能为空的对角边序列(称为snake)组成。
对编辑图顶点网格中的对角线进行编号,使对角线k由其对应的点(x,y)组成x-y=k。根据这个定义,对角线的编号范围是从-M到N。请注意,起点在对角线k上的垂直(水平)边的终点在对角线k-1(k+1)上,并且在对角线上保留一条蛇形开始。
引理1:D-路必须以对角k∈{-D,-D+2。D-2,D}。
证明:
0-路径仅由对角线边组成,从对角线0开始。因此它必须以对角线0结束。假设归纳地说,D-路径必须在{-D,-D+2 . . . D-2,D}中的对角线k上结束。每条(D+1)-路径由前缀D-path(以所述对角线k结尾)、非对角线边(以对角线k+1或k-1结尾)和蛇(也必须以对角线k+1或k-1结尾)组成。然后,每个(D+1)-路径必须在{(-D)±1,(-D+2)±1,….D-2)±1,(D)±1}={-D-1,-D+1。D-1,D+1}的对角线上结束。
因此,归纳法的结果是成立的。
引理表明,当D为奇数时,D-路仅在奇数对角线上结束,当D为偶数时,D-路仅在奇数对角线上结束。当且仅当D-路径是以对角线k结尾的D-路径之一时,D-路径在对角线k中到达的最远
点具有所有此类路径中可能最多的行(列)数。非正式地,在所有以对角线k结束的D-路径中,它的结束距离原点最远(0,0)。以下引理给出了最远到达D-路径的归纳刻画,并体现了贪婪原理:最远到达D-路径是通过贪婪地扩展最远到达(D-1)路径来获得的。
引理2:最远到达0的路径在(x,x)处结束,其中x是min(z-1 | | A z≠bz或z>M或z>N)。在不丧失一般性的情况下,可以将对角线k上最远到达的D-路径分解为对角线k-1上最远到达的D-1-路径,接着是水平边,接着是可能的最长蛇形或它可以分解为对角线k+1上的最远到达(D-1)路径,然后是垂直边,最后是可能最长的蛇形。
证明:
0-路径的基础很简单。如前所述,D路径由(D−1)路径、非对角边和蛇组成。如果D-路径在对角线k上结束,则(D-1)-路径必须在对角线k±1上结束取决于垂直边缘还是水平边缘位于最终蛇之前。最后一条蛇必须是最大的,因为如果蛇可以被延伸,D-路径不会是最远的。假设(D-1)-路径不是对角线上最远的。但是,进一步的到达(D-1)路径可以通过适当的非对角移动连接到D路径的最后一条蛇。因此,D-路径总是可以根据需要进行分解。✄
给定对角线k+1和k-1中最远到达(D-1)-路径的端点,分别为(x’,y’)和(x’,y“),引理2给出了计算对角线k中最远到达D-路径端点的过程。即,在对角线k中取(x’,y’+1)和(x“+1,y”)的进一步到达,然后沿着对角线边缘,直到不再可能这样做或直到到达编辑图的边界为止。此外,根据引理1有只有D+1条对角线中D-路径可以结束。这建议计算相关D+1对角线中D-路径的端点,以连续增加D的值,直到对角线N-M中的最远到达路径到达(N,M)。
For D ← 0 to M+N Do
For k ← −D to D in steps of 2 Do
Find the endpoint of the furthest reaching D-path in diagonal k.
If (N,M) is the endpoint Then
The D-path is an optimal solution.
Stop
当遇到最小的D时,上面的步骤将停止,对于最小的D,有一个到达(N,M)的最远的D-路径。
这必须在外部循环终止之前发生,因为D必须小于或等于M+N。通过构造,此路径必须相对于其内部的非对角边数最小。因此,这是解决LCS/SES问题。
在展示下面图2中的详细算法时,使用了一些简单的优化。一个数组V包含元素V[-D]、V[-D+2]、。,V[D-2],V[D]。根据引理1,这组元素与(D+1)路径的端点将被存储的那些元素不相交在外层循环的下一次迭代中。因此,阵列V可以同时保持D-路径的端点,而(D+1)路径的端点是从它们计算出来的。此外,要在对角线k中记录端点(x,y),则只保留x就足够了,因为y是已知的x-k。因此,V是一个整数数组,其中V[k]包含对角线k中最远到达路径端点的行索引。

作为一个实际问题,该算法搜索D≤MAX的D-路径,如果没有这样的路径达到(N,M),则它报告第14行中a和B的任何编辑脚本必须大于MAX。通过将常数MAX设置为M+N。
如上所述,该算法保证能够找到LCS/se的长度。图3说明了将该算法应用于图1的示例时搜索的D 路径。注意一个虚构的端点,(0,-1),在算法的第1行中设置,用于查找最远到达0路径的端点。还要注意的是,随着算法的发展,D-路径从编辑图的左下边界延伸。假设该区域没有对角线,则正确处理该边界位置。
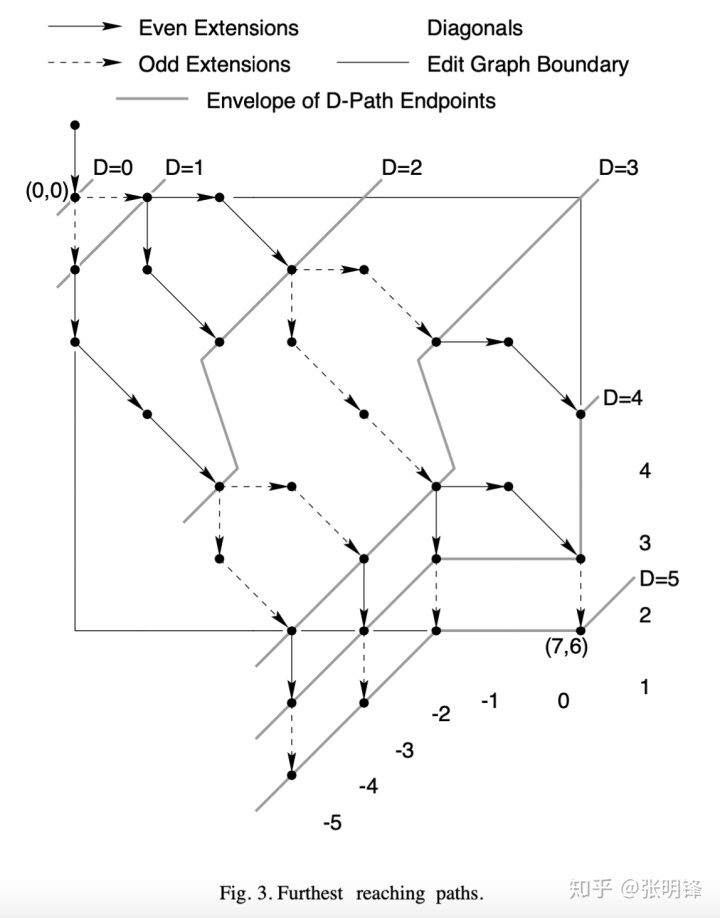
贪婪算法所需时间最多为O((M+N)D)。第1行和第14行消耗O(1)时间。内For循环(第3行)最多重复(D+1)(D+2)/2次,因为外For循环(第3行)重复D+1次,在第k次迭代中,内循环最多重复k次。除While循环(第9行)外,此内部循环中的所有行都需要恒定的时间。因此,O(D2)时间用于执行第2-8行和第10-13行。While循环是在最远到达路径的扩展中遍历的每个对角线迭代一次。但是,由于所有D-路径都位于对角线D和D之间,并且最多有(2D+1)min(N,M)个点,因此最多遍历O((M+N)D)个对角线在这个Band里。因此,该算法总共需要O((M+N)D)时间。注意,只有第9行,蛇行的遍历,才是限制步骤。算法的其余部分是O(D2)。此外,该算法从不需要超过O((M+N)MAX)在阈值MAX设置为远小于M+N的值的实际情况下的时间。
贪婪算法的搜索跟踪最优D-路径等。但V中只保留当前最远到达的端点集。因此,在第12行中只能报告SES/LCS的长度。到显式生成解路径O(D2)空间用于在每次外部循环迭代后存储V的副本。
设Vd为dth迭代后保存的V的副本。要列出从(0,0)到点Vd[k]的最佳路径,首先确定它是在沿着Vd-1[k+1]的垂直边或水平边的最大蛇的末端从Vd-1[k-1]。具体来说,假设是Vd-1[k-1]。递归地列出从(0,0)到这个的最佳路径
点,然后列出垂直边缘和最大蛇形到Vd[k] 是的。当d=0时递归停止,在这种情况下列出了从(0,0)到(V0[0],V0[0])的蛇。因此,在O(M+N)附加时间和O(D2)空间下,一条最优路径可通过将第12行替换为以VD[N-M]作为初始点调用此递归过程来列出。下一节将显示只需要O(M+N)空间的求精度。
如第2节所述,LCS/SES问题可以看作是加权编辑图上的单源最短路径问题的一个实例。这表明一个有效的算法可以通过专门化Dijkstra算法[3]。基本练习[2:207-208]表明,该算法需要O(ElgV)时间,其中E是边数,V是主题图中的顶点数。对于编辑图E<3V,因为每个点最多三个。此外,lgV项来自于管理优先级队列的成本。在当前的情况下,优先级将是[0,M+N]中的整数,因为边缘成本是0或1,并且到任何点的最长可能路径是 M+N.在这些条件下,可以使用“bucket”和链表技术在恒定时间内实现优先级队列操作。因此,Dijkstra的算法可以专门用于在
编辑图中的顶点数,即O(MN)。最后的改进源于注意到所需要的是从源(0,0)到点(M,N)的最短路径。Dijkstra算法确定最小距离 从源的顶点按递增顺序,每次迭代一个顶点。在引理1中,与(0,0)的距离小于(M,N)的O((M+N)D)点最多,并且先前的改进将每次迭代的代价降低到O(1)。
因此,只要确定到(M,N)的最小距离,算法就可以停止,并且只需花费O((M+N)D)时间。
结果表明,Dijkstra算法的一个特殊化也给出了LCS/SES问题的一个O(ND)时间算法。然而,生成的算法包含一个相对复杂的离散优先级队列,队列可能包含多达O(ND)个条目,即使在计算LCS/se的长度时也是如此。有人可能会说,进一步的细化导致了本文的简单算法,但是变得如此脆弱,因此本节中使用的直接且容易激发的推导是可取的。讨论的目的是揭示最短路径与LCS/SES问题及其算法之间的密切关系。
四。改进
基本算法可以通过多种方式进行修饰。首先,该算法的期望性能为
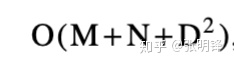
,远优于O(M+N)D的最坏情况预测。尽管这里没有显示,实验结果表明,平均值的方差很小,尤其是当字母表的大小变大时。因此,虽然有些病理病例需要O((M+N)D)时间,但它们是极为罕见的(如O(N2)问题 快速排序)。其次,该算法可以改进为在报告编辑脚本时仅使用线性空间。另一个被证明可以接受这种改进的算法是基本的O(MN)动态规划算法。线性空间算法具有重要的实用价值,因为许多大问题可以在O(D2)时间内合理地求解,而在O(D2)空间则不能。最后,
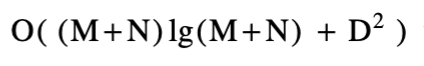
最坏情况的时间变化是通过使用一些先前开发的技术加速蛇的穿越而获得[6,14]。变化是由于这些基本方法的复杂性,这是不切实际的,但其优越的渐近最坏情况复杂性具有理论意义。
4a.概率分析
考虑序列A和序列B在最短编辑脚本问题中的随机模型。A和B是一个字母表∑上的序列,其中每个符号出现的概率为pσ(对于σ∈∑)。A的N个符号是根据概率密度pσ随机独立选择。通过从A中随机删除δ符号并随机插入随机选择的符号,获得M=N-δ+ι符号序列B。这个选择删除和插入位置的概率是一致的。等效模型是生成长度为L=N-δ的随机序列,然后将δ和ι随机生成的符号随机插入到该序列中,分别生成a和B。注意,A和B的LCS必须至少由L个符号组成,但可能更长。
另一种模型是将A和B看作长度为N和M的随机生成序列,该序列被压缩为长度为L的LCS。该模型不等同于上述模型,除非在尺寸of∑变为任意大,每个概率pσ变为零。尽管如此,随后的处理方法也可以应用于该模型,且具有相同的渐近结果。选择第一个模型是因为它反映了SES问题假设的用于将A映射到B的编辑脚本。而其他编辑脚本命令,如“传输”,“移动”和“交换”更能反映实际的编辑会话,它们的包含会导致与本文讨论的SES问题截然不同的优化问题。因此,基于这种编辑过程的随机模型不是考虑过的。
在A和B的编辑图中,有L条对角边对应于A和B的随机生成的LCS、 以(x,y)结尾的任何其他对角线边出现的概率与这些符号出现x=by的概率相同通过独立随机试验获得。因此,非LCS对角线的概率为:
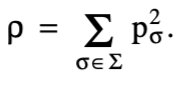
。SES算法通过扩展最远到达路径直到到达点(N,M)进行搜索。每个分机包括一条水平或垂直的边缘,后面跟着可能最长的蛇形。最大的蛇形由许多LCS和非LCS对角线。在一个给定的延拓蛇中有确切的t off LCS对角线的概率是
pt(1-ρ)。因此,扩展中的非LCS对角线的预期数量是
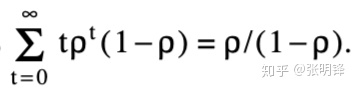
。在SES算法的外For循环的dth迭代中,最多进行d+1扩展。因此最多
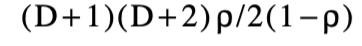
off-LCS对角线在预期情况下被遍历。此外,最多可遍历L LCS图。因此,算法的临界While循环平均执行O(L+D2)。
当ρ从1有界时的次数。算法的其余部分已经被观察到在最坏的情况下
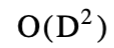
时间。当ρ=1时,字母表∑中只有一个概率为非零的字母,因此A和B由重复那部分字段,概率为1。在这种情况下,算法在O(M+N)时间内运行。因此,在预期情况下,SES算法需要
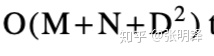
时间。
4b.线性空间优化
LCS/SES问题相对于编辑图边的方向是对称的。考虑反转for序列A和B。A和B的子序列和编辑脚本在此反向编辑图中仍然建模为路径,但现在路径开始于(N,M)并结束于(0,0)。此外,对路径的解释会稍微改变,以反映方向的反转。从(x,y)开始的每一条对角线边都给出一个符号,
在公共子序列中的x(=by);点(x,y)的每个水平边对应于删除命令“x D”等。因此,LCS/SES问题可以通过从(N,M)开始并逐渐扩展到最远的位置来解决到达反向编辑图中的路径,直到到达(0,0)。此后,正向路径将引用编辑图中的路径,反向路径将引用反向编辑图中的路径。因为相反方向的路径精确对应,路径的方向只有在具有操作重要性时才能被区分。
在Hirschberg[7]的线性空间算法中,采用了分而治之的策略。D-路径有D+1条蛇,其中一些蛇可能是空的。分割步骤需要找到最佳D-路径。这样做的目的是同时在正向和反向运行基本算法,直到最远的正向和反向路径从相反的拐角处开始“重叠”。引理3提供了这种方法的形式观察。
引理3:当且仅当存在从(0,0)到某点(x,y)的[D/2]路径和从某点(u,v)到(N,M)的[D/2]路径时,存在从(0,0)到(N,M)的D-路径.

证明:
假设有一条从(0,0)到(N,M)的D-路径。它可以在中间蛇的开始(x,y)处分成从(0,0)到(x,y)的[D/2]路径和从(u,v)到(N,M)的[D/2]路径,其中(u,v)=(x,y)。从(0,0)到(u,v)的路径
最多可以有u+v非对角边,并且存在到(u,v)的[D/2]-路径,这意味着u+v≥[D/2]。从(x,y)到(N,M)的路径最多可以有(N+M)-(x+y)个非对角边,并且存在到(x,y)的[D/2]-路径,这意味着
x+y≤N+M-[D/2]。最后,u-v=x-y且u≤x as(x,y)=(u,v)。
相反,假设存在[D/2]-和[D/2]-路径。但u≤x意味着从(0,0)到(u,v)存在k-路径,其中k≤[D/2]。根据引理1,∏=[D/2]-k是2的倍数,因为k-路径和[D/2]-路径都在同一对角线中结束。此外,当u+v≤[D/2]时,k-路径具有(u+v~-k)/2~∏/2对角线。通过用一对水平边和垂直边替换k-路径中的每一条对角线的∏/2,得到了从(0,0)到(u,v)的[D/2]路径。但是有一个从(0,0)到(N,M)的D-路径,由这个[D/2]-路径到(u,v)和给定的[D/2]-路径从(u,v)到(N,M)组成。注意,[D/2]-路径是这个D-路径的一部分。通过对称参数,[D/2]-路径也是从(0,0)到(N,M)的D-路径的一部分。
下面的概要给出了寻找最优路径中间蛇的过程。对于D的连续值,从(0,0)计算最远到达的正向D-路径的端点,然后从(N,M)计算最远到达的反向D-路径。在V向量中这样做,每个方向一个,如在基本算法中。在计算每个端点时,检查它是否在相同的对角线方向上与路径重叠,但方向相反。需要检查以确保给定对角线中存在相反的路径,因为正向路径位于对角线中心约0处,反向路径位于以∏=N-M为中心的对角线中。此外,根据引理1,最佳编辑脚本长度为奇数或偶数,因为∏为奇数或偶数。因此,当∏为奇数时,仅在延伸时检查重叠正向路径,当∏为偶数时,仅在延伸反向路径时检查重叠。当一对相对的和最远的到达路径重叠时,停止并报告重叠的蛇形为最佳路径。请注意,可以很容易地传递此蛇的端点,因为在上一步中刚刚计算了该蛇形。

这个过程的正确性在很大程度上依赖于引理3。在不丧失一般性的前提下,假设∏为偶数。当遇到最远到达相反方向的D-路径的最小D时,算法立即停止重叠。首先,必须证明重叠路径满足引理3的可行性条件。假设反向最远到达路径在(u,v)处结束,其中u+v=k。始终存在非对角边的k路径(0,0)到(u,v),当与反向D-路径组合时,形成从(0,0)到(N,M)的k+D-路径。这个路径和引理3意味着存在重叠的h-路径,其中h=(k+D)/2(k+D可被2整除,因为∏是偶数)。当然可以存在重叠的最远到达h或更少的路径。如果k<D,则h<D与最远到达的D-路径是最先重叠的事实相矛盾。所以u+v≥D。一个类似的论点表明,最远的距离正向D-路径也满足引理3的可行性约束。现在,可行的,重叠的D-路和引理3意味着有一个长度为2D的解路,如果有2k路,k<D,那么引理意味着有k-路径重叠。但这意味着存在最远到达k或-较少的重叠路径,这与较小D没有重叠路径的事实相矛盾重叠路径是从(0,0)到(N,M)的最优2D路径的一部分。当∏为奇数时,也可以得出同样的结论。仍然需要证明,选择的蛇是最优路径的中间蛇,它是最优路径的一部分。如果∏是奇数(偶数)则此蛇是正向(反向)路径的D+1,该路径是最优2D-1(2D)路径的一部分。无论哪种情况,蛇形都是[k/2]+1st包含它的最优k-路的。
寻找最优D-路径中间蛇的过程需要两个V-向量的总O(D)工作存储器。该过程只需要O((M+N)D)时间,因为正向和反向路径扩展这两个部分通过基本算法使用的相同参数消耗O((M+N)D)时间。事实上,在向前和向后扩展路径时,蛇的数量可以是基本算法的一半,因为只有D/2搜索对角线。实验结果表明,当D=0时,该算法与基本算法相比具有同样的效率,且速度比D快一倍增加。
给出了中间蛇形过程,设计了一种通过N和M大小的a和B的编辑图寻找最优路径的线性空间算法。为了简单起见,下面的分治算法只列出了a和B的一个最长的公共子序列(生成一个最短的编辑脚本作为练习留下)。首先,通过找到一条中间蛇来划分问题,比如说,从最优D-路径的(x,y)到(u,v)。开始克服这个问题,通过
递归地查找从(0,0)到(x,y)的✻D/2✼-路径并列出其LCS。然后列出中间的蛇(如果u<x,则“Output A[x..u]”不列出任何内容)。最后,递归地找到从(u,v)到(N,M)的✽D/2✾路径并列出其LCS。这个
递归以两种方式结束。如果N=0或M=0,则L=0,则无需列出任何内容。在另一种情况下,N>0,M>0,D≤1。如果D≤1,则通过删除或插入至多一个符号从A获得B。但随后A和B中较短的是LCS,应该列出。

设T(P,D)为算法所花费的时间,其中P为N+M。因此T满足递推线质量:
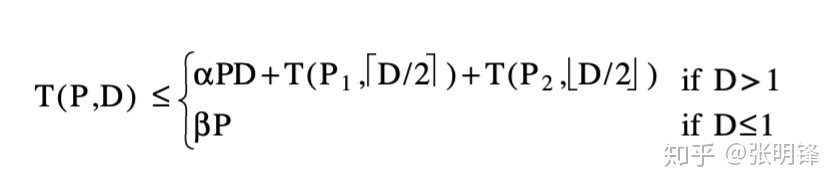
其中P1+P2≤P,α和β是合适的大常数。注意到当D≥2时,[D/2]≤2D/3,一个直接的归纳论证表明T(P,D)≤3αPD+βP,因此分治算法仍然需要O((M+N)D)时间,尽管它通过❈lg D❉递归级别下降。此外,该算法只需要O(D)工作存储器。中间snake过程需要两个O(D)空间V向量。但这一步是在进行递归之前完成的。因此,过程的所有调用只共享一对全局V向量。此外,只遍历O(lgD)级别的递归,这意味着只需要O(lgD)存储
在递归堆栈上。不幸的是,输入序列A和B必须保存在内存中,这意味着总共需要O(M+N)空间。
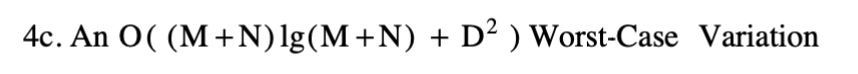
最后一个主题涉及两个先前的结果,每个结果都在这里略述过。首先,后缀树被用来有效地记录被比较序列的公共子列表。术语子列表用作与强调符号必须连续的子序列相反。第二,一种基于RAM的固定V顶点树最低公共祖先点在线查询的算法取O(V+Q)时间。有效的变异集中在快速找到从点(x,y)开始的最大蛇的长度或端点。这被证明是为了找到后缀树中两片叶子的最低共同祖先。这个类别使用上述两种技术,在每个查询的O((M+N)lg(M+N))预处理时间和O(1)时间内完成。接下来的段落修饰了这些想法。
一个长度为L的序列S的后缀树或Patricia树[12,14]具有用S的子列表标记的边、用S的位置标记的叶,并且满足以下三个性质。
1。将从根到叶的路径上遍历的边缘标签连接到位置j,得到从j开始的S的后缀S[j..L],因此树中的每个路径都表示S的子列表。
2。每个内部顶点的向外度都大于1。
3。每个顶点外边缘的标签都以不同的符号开头。
只有当S的最后一个符号与S中的其他符号不同时,才能满足这些属性。通常通过在目标序列中附加一个特殊符号来满足此条件,并且一旦满足,后缀树是唯一的。
属性2保证有少于L个内部顶点。此外,标记边缘的子串可以通过在S中存储其第一个和最后一个字符的索引来表示,因此后缀树可以存储在O(L)中空间。后缀树的有效构造超出了本文的研究范围。读者可以参考McCreight的一篇论文,该论文给出了一个算法,该算法在O(L)步中构造一个后缀树。大多数步骤都很容易完成在O(1)时间内,但有些需要根据第一个符号选择出边。当alpabet是有限的时,顶点的出度是有限的,选择需要O(1)时间。当字母表不受限制时,高度平衡树或其他一些最坏情况下有效的搜索结构允许在O(lgL)时间内进行选择。因此,后缀树的构造对于有限的字母表需要O(L)时间,否则需要O(LlgL)时间。
考虑从S的后缀树的根到叶子i和j的两条路径。从根到i和j的共同祖先的每条路径表示后缀S[i..L]和S[j..L]的共同前缀。从属性3可以看出到i和j的最低共同祖先的路径,表示它们各自后缀的最长前缀。这一观察结果激发了编辑图中从点(x,y)开始的最大蛇的下列后缀树特征长度分别为N和M的A和B。形成序列S=A.$1.B.$2的位置树,其中符号bols$1和$2不相等或A或B中的任何符号。表示从(x,y)开始的最大蛇从S的后缀树的根到位置x和y+N+1的最低公共祖先的路径。这是因为$1和$2都不能作为后缀a[x..N]$1.B.$2的最长公共前缀的一部分。
和B[y..M].$2.。所以要找到一条蛇的终点,从(x,y)开始,找到叶子x和后缀树中的y+N+1,并返回(x+m,y+m),其中m是子列表的长度,由指向该索引的路径表示。在线性预处理过程中,计算每个顶点的子列表长度和辅助结构构造了Harel和Tarjan的O(V+Q)最低共祖算法所需的参数。这种基于RAM的算法需要O(V)的预处理时间,但是可以在O(1)的时间内回答每个在线查询。因此,在O((M+N)lg(M+N))预处理时间(构建后缀树是主要代价)下,对最大snakes端点的在线查询集合可以在每次查询的O(1)时间内得到响应。
修改第3节的基本算法,方法是(a)用最大snake查询所需的预处理对其进行前置,(b)用O(1)查询原语替换第9行。回想一下,除第9行外,最内层循环中的每一行都是O(1),循环重复O(D2)次。现在第9行需要0(1)次
修改后的算法在O((M+N)lg(M+N)+D2)时间内运行。请注意,这种变化主要是理论上的兴趣。算法片段的比例系数要大得多这意味着在变化变得更快之前,问题必须非常大。但是后缀树的空间效率特别低,快速最小共同祖先算法需要两个大小相等的辅助树。因此,对于大到足以节省时间的问题,很可能没有足够的内存来容纳这些额外的结构。