前言

排序是很重要的一个算法，在现实生活中也处处都有它的身影，诸如网上购物按价格排序、学校考试名次的排名……排序应用的场景都很多，本章介绍

插入排序、选择排序、冒泡排序、希尔排序、归并排序、堆排序、快速排序

。

一、冒泡排序

冒泡排序的思想很简单，无非就是分成多趟排序，每一趟排序按照需求（升序或降序）把最大或最小的元素排到最后面，每趟排序从第一个元素开始两两比较，大的或小的往后挪，排完一趟后最后一个元素是有序的了，所以下一趟排序最后一个元素不参与排序。

代码实现：

//交换两个数
void Swap(int* e1, int* e2)
{
	int tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

// 冒泡排序
void BubbleSort(int* a, int n)
{
	//n个元素，需要走n-1趟
	for (int i = 0; i < n - 1; i++)
	{
		//每趟
		for (int j = 0; j < n - 1 - i; j++)
		{
			if (a[j] > a[j + 1])
			{
				Swap(&a[j], &a[j + 1]);
			}
		}
	}
}

这里排的是升序，注意每趟的比较次数，第一趟比较次数为

n-1

次，第一趟排完已经有一个元素是有序了，所以第二趟待排序的个数就是

n-1

个，而

n-1

个比较

n-1-1

次就行了，利用每趟走完

i++

这一点，

j<n-1-i

正正好。

代码优化：

对于冒泡排序还是可以优化一下的，在待排序的数据是有序的状态下，以上代码还是会乖乖的一步一步比较走完，白白浪费了时间，所以我们来优化一下，假设一个变量

flag

为

1

，如果在某一趟中，没有进入交换循环，那也就表示当前数据是有序的了，接下来也就不再需要比较了，如若无序，

flag

变为

0

，则进入下一趟再把

flag

置为

1

。

优化代码如下：

//交换两个数
void Swap(int* e1, int* e2)
{
	int tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

// 冒泡排序
void BubbleSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int flag = 1;
		//判断数组是否已经有序
		for (int j = 0; j < n - 1 - i; j++)
		{
			if (a[j] > a[j + 1])
			{
				Swap(&a[j], &a[j + 1]);
				flag = 0;
			}
		}
		if (flag)
			return;
	}
}

二、选择排序

选择排序的思想也很简单，按照升序或者降序，每次比较选择最小的元素或者最大的元素，然后与第一个元素交换，然后再比较选择次大或是次小的元素，与第二个元素交换，依此直至数据全都排序完成。

代码如下：

//交换两个数
void Swap(int* e1, int* e2)
{
	int tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

// 选择排序
void SelectSort1(int* a, int n)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		//假设第一个元素的下标的最小的
		int mini = begin;
		for (int i = begin + 1; i <= end; i++)
		{
			if (a[i] < a[mini])
				mini = i;
		}
		//最小的元素与最大的元素交换
		Swap(&a[begin], &a[mini]);
		begin++;
	}
}

这里排的是升序，注意end的取值是

n-1

，因为下面

i

是从

begin+1

开始的，

end

如果取

n

的话，当

begin

为最后一个元素的下标时，此时的

i+1

会导致越界，所以

end

取值为

n-1

，当倒数第二个元素有序时，倒数第一个元素也就有序了。

代码优化：

这里如果我们排升序的话，每次只取最小的元素放在最前面，这样效率不高，所以我们每次取最小的元素和最大的元素，也就相当于一次就排好了两个元素，这样效率会高一些。

优化代码如下：

//交换两个数
void Swap(int* e1, int* e2)
{
	int tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

// 选择排序
void SelectSort(int* a, int n)
{
	//每趟选出最小的和最大的
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		//记录该躺最小的值的下标
		int mini = begin;
		//记录该躺最大的值的下标
		int maxi = begin;
		for (int i = begin + 1; i <= end; i++)
		{
			if (a[i] < a[mini])
				mini = i;
			if (a[i] > a[maxi])
				maxi = i;
		}
		Swap(&a[begin], &a[mini]);
		//预防该躺最大的值就在begin
		if (begin == maxi)
			maxi = mini;
		Swap(&a[end], &a[maxi]);
		begin++;
		end--;
	}
}

这里我们需要注意，下面两行代码的作用是为了防止当最大元素的下标与当前

begin

相等时，此时说明最大的元素是在

begin

位置，而我们的交换是先把最小的元素与

begin

位置的元素进行交换，此时最小的元素去到了

begin

位置，而

begin

原本保存了最大的元素，所以最大的元素又与

mini

位置的元素进行了交换，此时如果

maxi

位置要与

end

位置进行交换时，显然是不对的了，因为原本

maxi

位置的值已经被移动到了

mini

的位置，所以当

begin

与

maxi

相等时，在

mini

位置的值与

begin

位置的值进行了交换后，最大的值跑到了

mini

的位置下，那么

maxi

就应该等于

mini

，这样

maxi

再与

end

交换，此时才是正确的

//预防该躺最大的值就在begin
if (begin == maxi)
	maxi = mini;

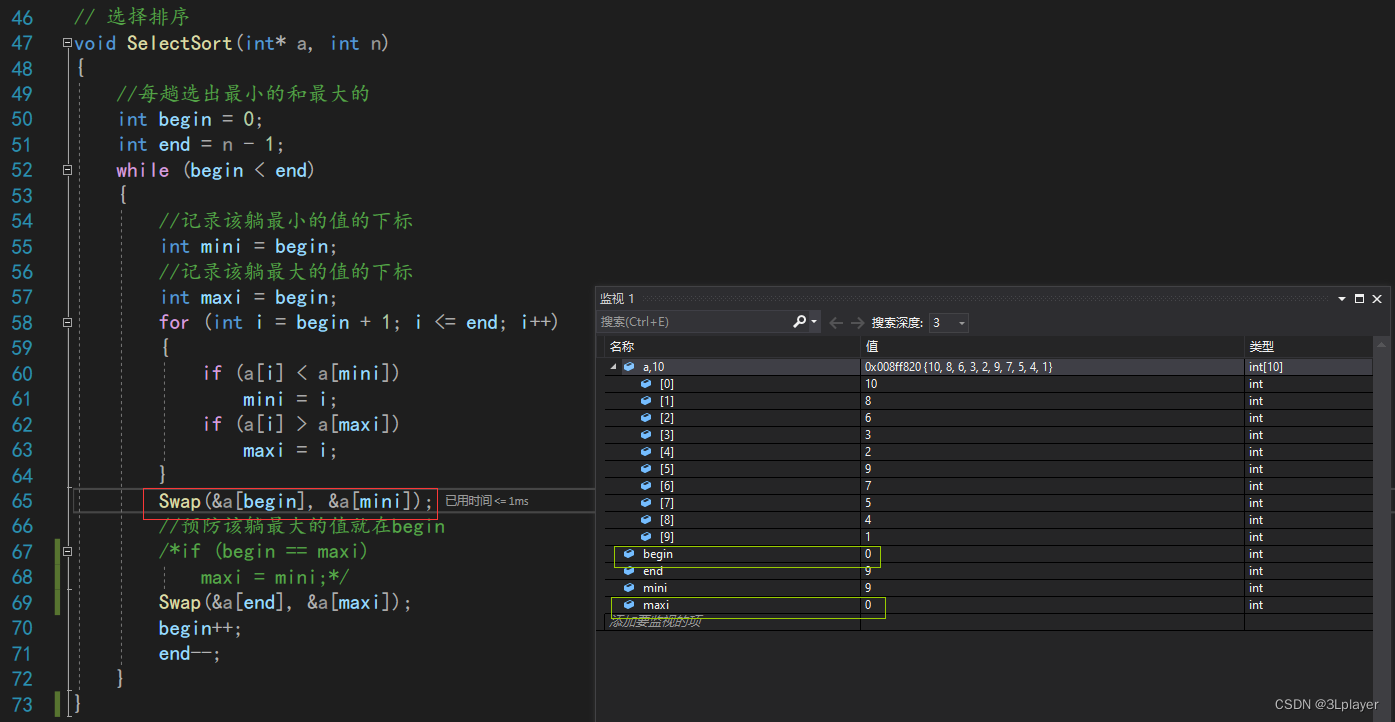
错误举例：

1）此时

begin

与

maxi

是相等的，可以看到最大值是存储在下标为

0

处，然后走到红色框处，执行第一次交换，也就是最小值与

begin

的交换。

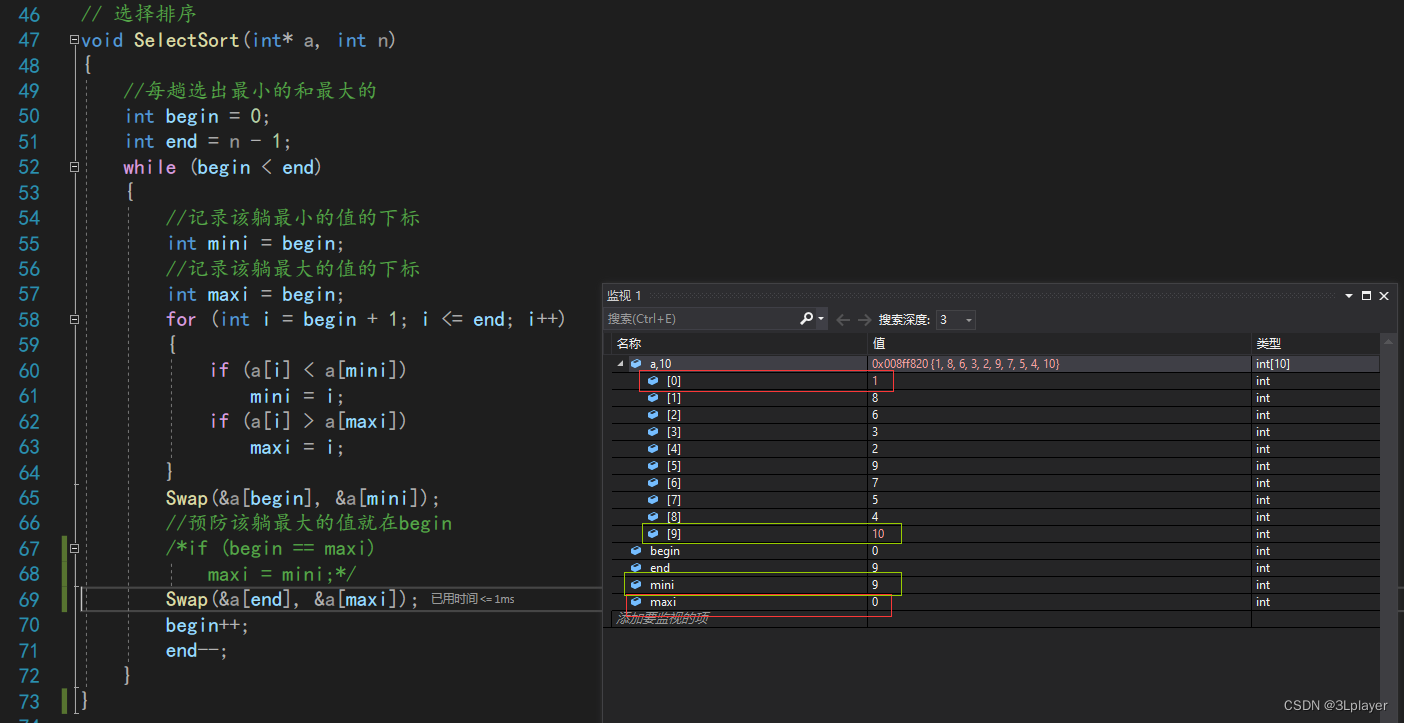
2）此时最小值已经与

begin

交换，可以看到最小值已经移动到了正确的位置，但是原本的最大值却移动到了下标为

9

处，那么此时

maxi

所指向的下标处存储的就不是最大值了，这样就会导致排序出错，所以当

maxi

与

begin

相等时，

maxi

应该等于

mini

，这样排序才正确。

三、插入排序

插入排序的思想并不难，无非就是插入一个数，然后判断该数的前面有多少个大于或小于该数的数，然后挪动这些数，最后将该数再插入到合适的位置即可。

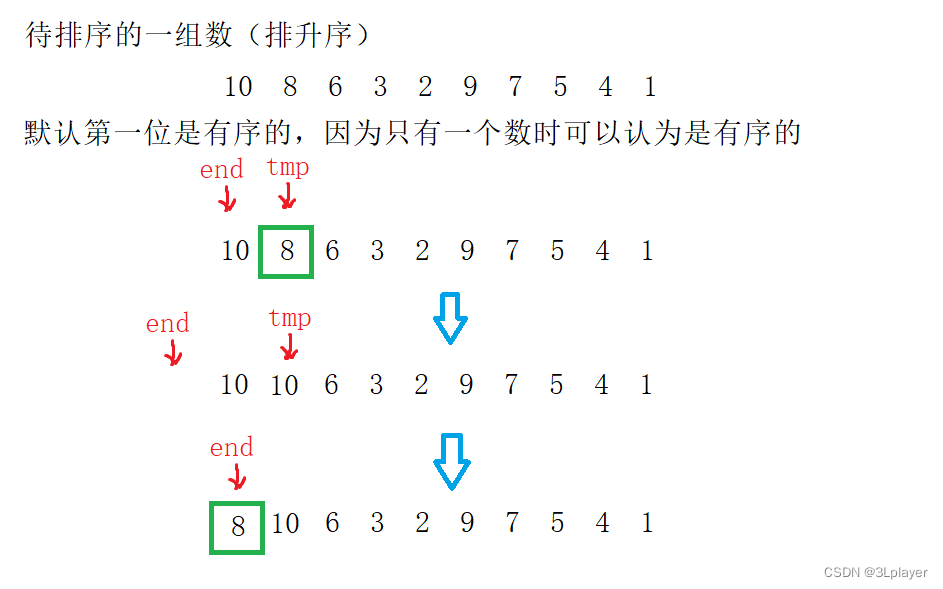
画图举例：

这是第一次排序，结合代码来看很容易理解，我们要排的是升序，循环条件是

end >= 0

，而此次的

end

是

0

，

tmp

存储

end

的下一位，当

tmp < end

时，将

end

移动到

end + 1

处，

end–

，再判断与

tmp

的大小关系，而当有一次

tmp > end

处的值时，该处就是

tmp

此次排序的合适位置，最终

tmp

所处的位置都是当前的

end + 1

处。

代码如下：

// 插入排序
void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				--end;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

四、希尔排序

希尔排序的大体思想是，先进行预排序，让较大的数先尽快的到达后面，而在进行的多趟预排后，数据已经趋近于有序了，最后一趟，也就是相当于插入排序了，但是此时的数据已经趋于有序，所以最后一趟会很快。

图例：

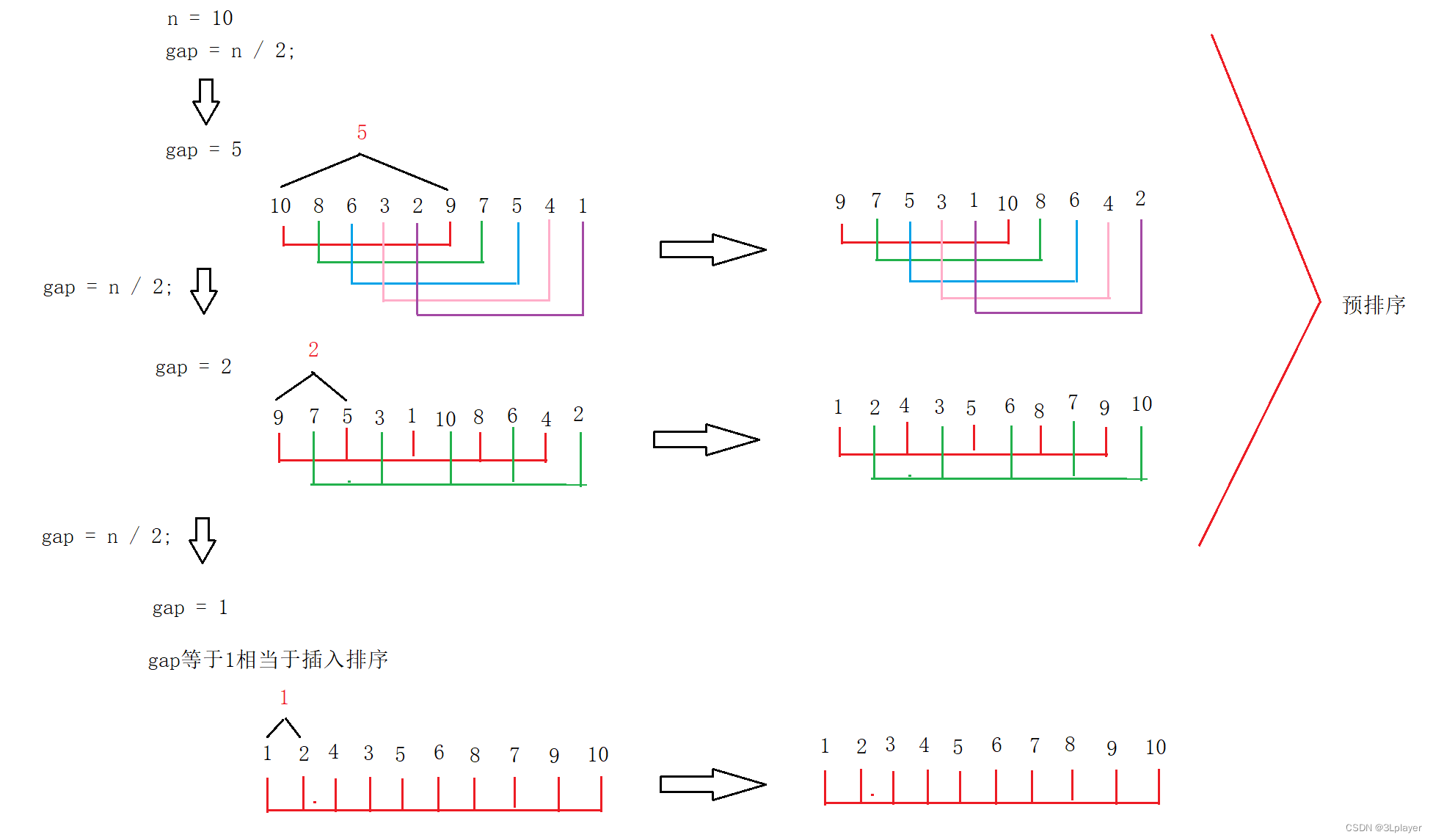
其中

gap

可以理解为间距。

代码如下：

// 希尔排序
void ShellSort(int* a, int n)
{
	int gap = n;
	//gap > 1（预排序）
	//gap == 1（直接插入排序）
	while (gap > 1)
	{
		gap /= 2;
		//gap = gap / 3 + 1; //需要+1才能确保某些情况的最后一次为1
		//单趟排序
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

五、归并排序

归并排序思想大致是这样子的，假设数据的左半部分是有序的，右半部分也是有序的，就对它的左半部分和右半部分比较，每次比较取小的把小的插入到一个数组中，然后当左半部分或者右半部分中的某一部分的元素已经取完了，剩下的直接依次插入数组的后面即可。

递归

递归求解就是把数据分为左半部分和右半部分，而左半部分又分为左半部分和右半部分……依此下去直到当前区间元素只剩一个元素或者一个元素都不剩，一个元素默认有序，然后排好序后往回归，最后回到最开始的左半部分和右半部分，此时左半部分和右半部分就都有序了，那么整体比较之后数据就有序了。

图例：

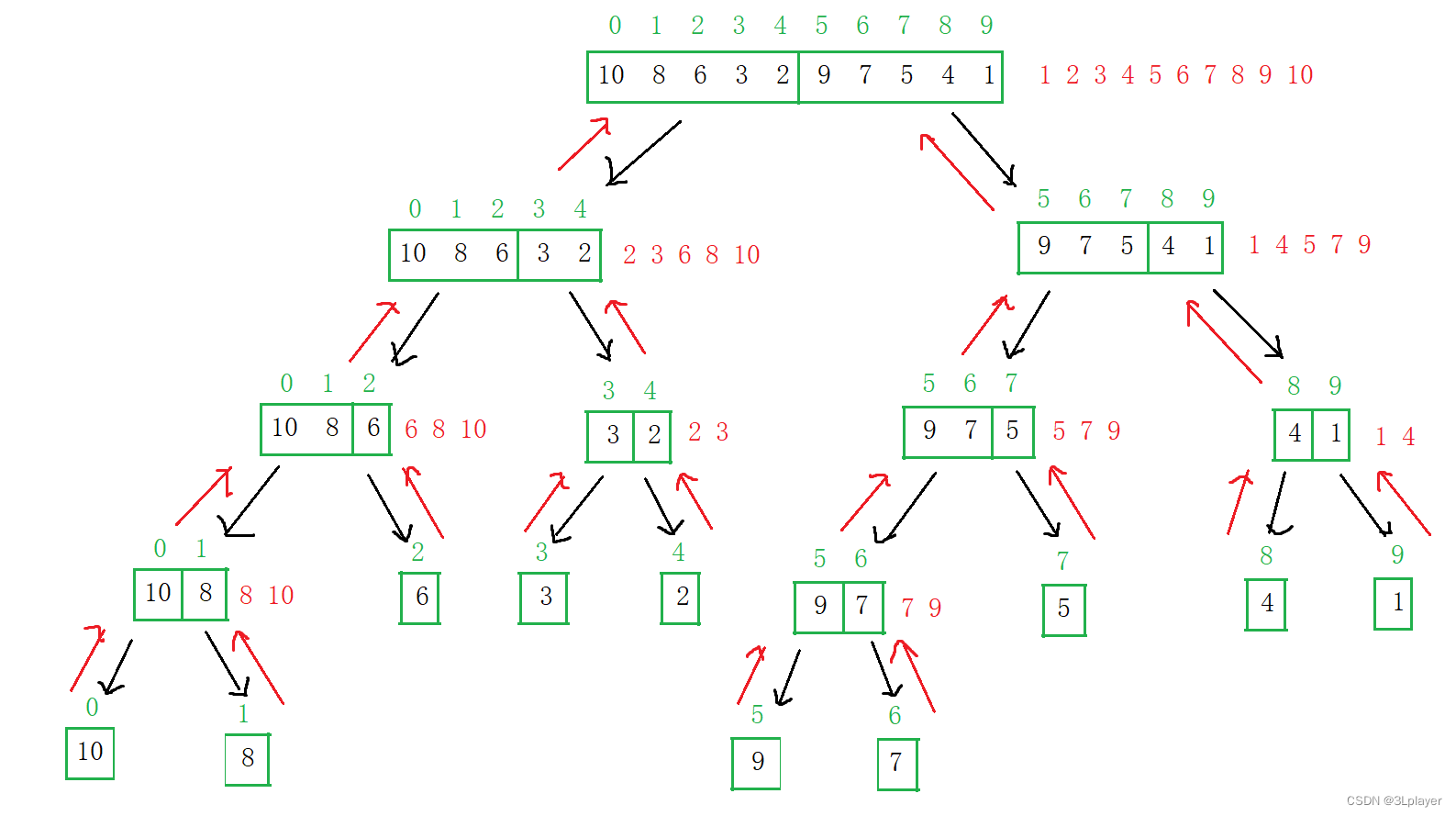
代码如下：

//归并递归
void ReMergeSort(int* a, int begin, int end, int* tmp)
{
	//本次递归只有一个元素
	if (begin >= end)
		return;
	//本次数组的中间下标
	int mid = begin + (end - begin) / 2;
	//递归左
	ReMergeSort(a, begin, mid, tmp);
	//递归右
	ReMergeSort(a, mid + 1, end, tmp);
	//左起点
	int begin1 = begin;
	//左终点
	int end1 = mid;
	//右起点
	int begin2 = mid + 1;
	//右终点
	int end2 = end;
	//记录tmp存储数据下标
	int i = begin;
	//判断两个待比较的有序数组都没走完
	//升序排序
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] <= a[begin2])
			tmp[i++] = a[begin1++];
		else
			tmp[i++] = a[begin2++];
	}
	//没走完的直接赋值
	while (begin1 <= end1)
		tmp[i++] = a[begin1++];
	while (begin2 <= end2)
		tmp[i++] = a[begin2++];
	//有序的部分copy回原数据
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

//归并排序
void MergeSort(int* a, int n)
{
	//tmp数组用于数组的中转
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (!tmp)
	{
		perror("malloc()");
		exit(-1);
	}
	ReMergeSort(a, 0, n - 1, tmp);
	free(tmp);
	tmp = NULL;
}

这里当递归到区间内的元素小于等于

1

时为结束标志，然后把已经比较过的有序的部分存入临时的数组

tmp

，再把

tmp

的数据拷贝回原数组，需要注意每一次存入

tmp

的数据都要拷贝回原数组。

非递归

非递归采用变量

gap

来控制每次左右两组的元素个数，

gap

从

1

开始，即左右两组中每组只有

1

个元素时默认其是有序的，然后归并，此时每两个都是有序的，然后每次

gap 乘等 2

，循环结束条件为

gap

大于等于

n

（元素个数）。

图例：

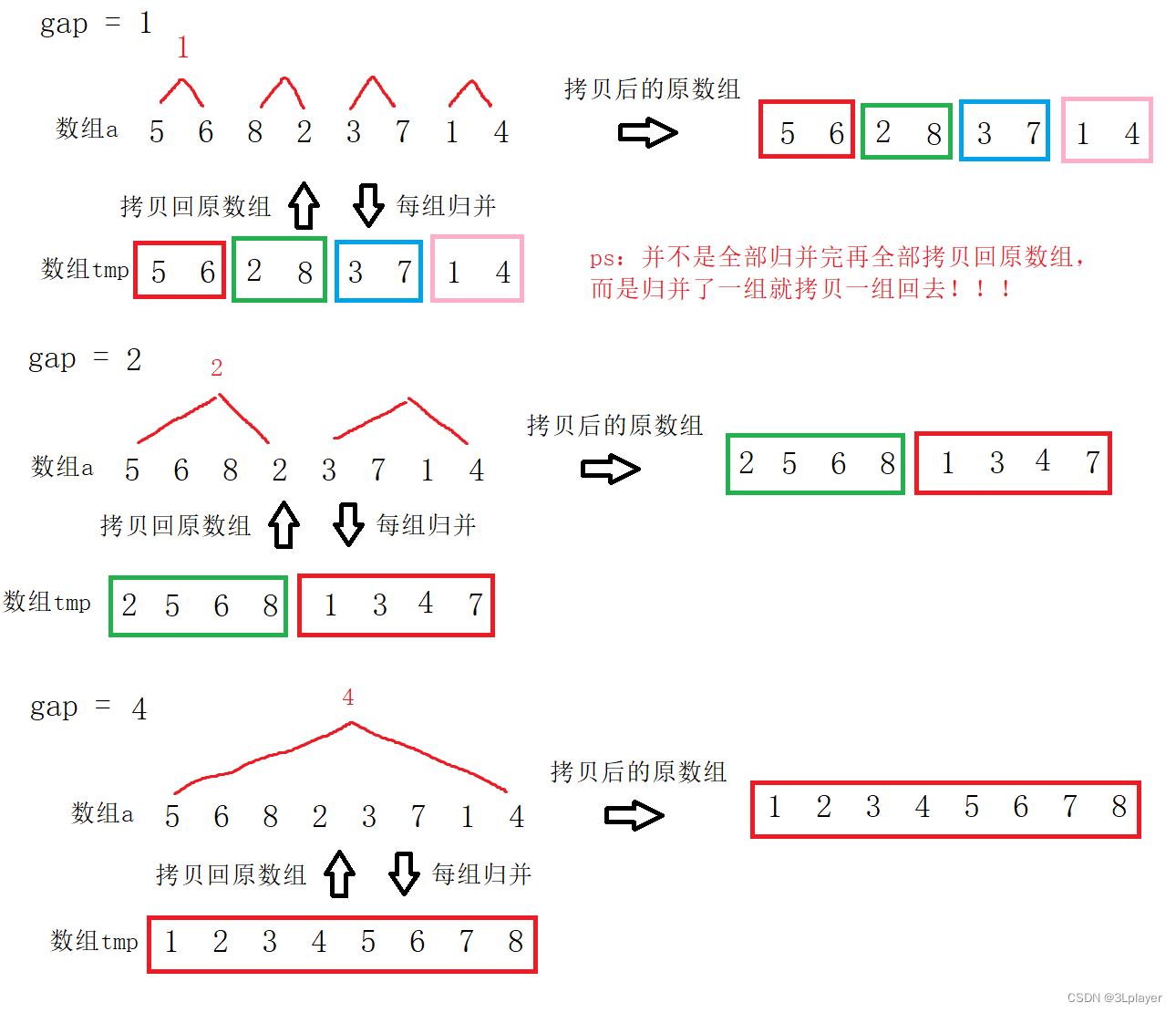
以上是

n

的个数为

2

的次方数时的情况，但如果

n

的个数不是

2

的次方数，则会出现越界情况，如下图所示：

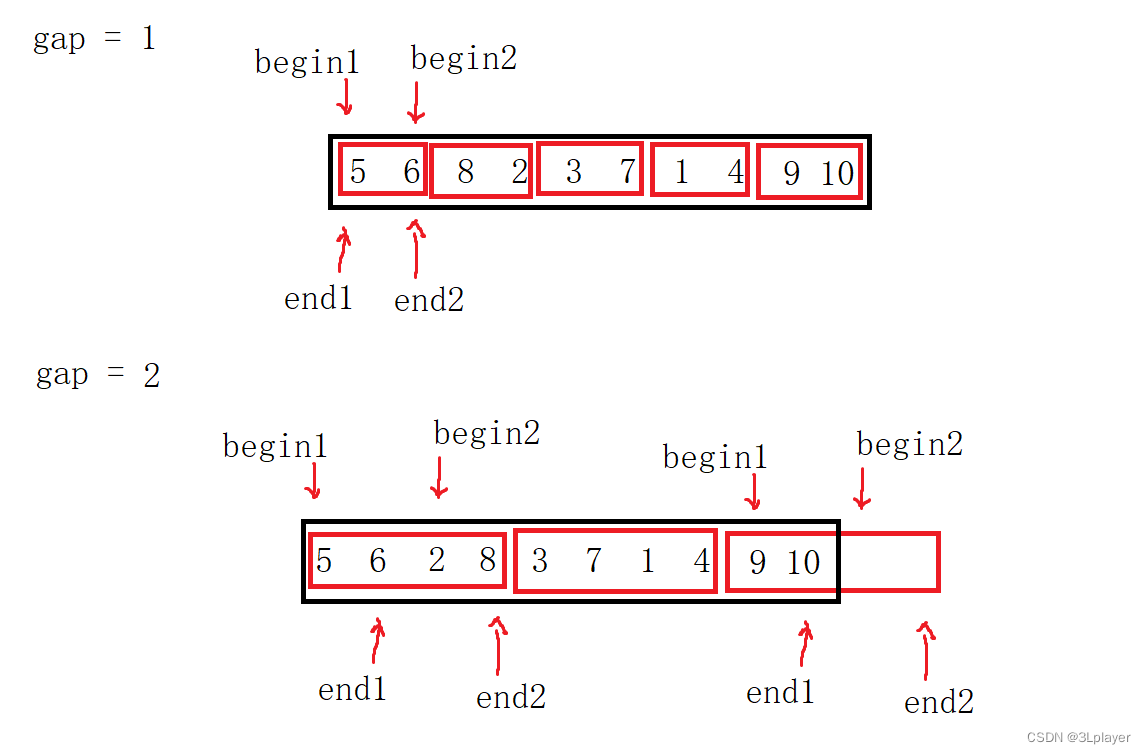
通过上图可以看到，但

n

为

10

时，不是

2

的次方数，此时就出现了越界情况，所以为了避免越界情况的发生，我们通过加上

if

语句即可解决。

代码如下：

//归并非递归
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (!tmp)
	{
		perror("malloc()");
		exit(-1);
	}

	//左右每组待比较的元素个数
	int gap = 1;

	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			//左半部分
			int begin1 = i;
			int end1 = i + gap - 1;
			//右半部分
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;

			//处理越界
			if (end1 >= n)
			{
				break;
			}
			else if (begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}
			
			//判断两个待比较的有序数组都没走完
			//升序排序
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
					tmp[i++] = a[begin1++];
				else
					tmp[i++] = a[begin2++];
			}
			//没走完的直接赋值
			while (begin1 <= end1)
				tmp[i++] = a[begin1++];
			while (begin2 <= end2)
				tmp[i++] = a[begin2++];
			//有序的部分copy回原数据
			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}
		gap *= 2;
	}

	free(tmp);
	tmp = NULL;
}

可能越界的情况有

三

种：

• 
  end1
  
  越界，直接
  
  break
  
  ，不用再比较，已经是有序的了。
• 
  begin2
  
  越界，直接
  
  break
  
  ，不用再比较，已经是有序的了。
• 
  end2
  
  越界，不能直接
  
  break
  
  ，因为
  
  begin2
  
  没有越界，那么
  
  begin2
  
  此区间还是有元素的，要和前面的
  
  begin1-end1
  
  此区间比较，所以
  
  end2
  
  赋值为
  
  n-1
  
  ，即最后一个元素的下标。

越界图示：

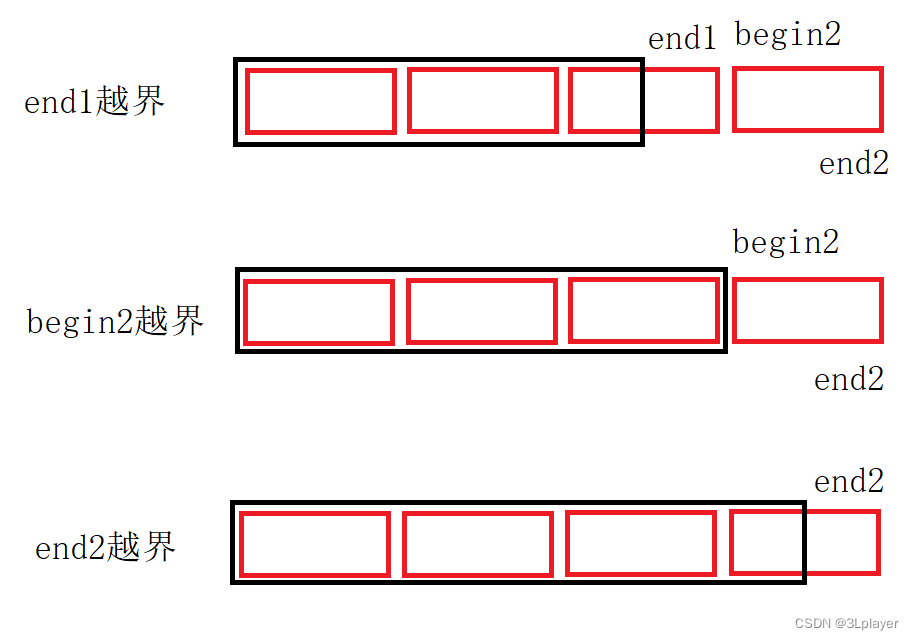
六、堆排序

堆排序的大体思想是，根据情况先建好堆，需要排升序就建大堆，需要排降序就建小堆，建好堆之后，根据堆的性质，堆顶元素是当前堆中最大或者最小的元素（根据建的是大堆还是小堆而定），把堆顶的元素移至最后，除去已经移至最后的元素，用剩下的元素重新建堆，以此往复，直至数据有序。

堆的定义：

//堆
typedef struct Heap
{
	int* data;//本体
	int size;//当前存储元素个数
	int capacity;//总个数
}Heap;

建堆：

这里排升序，所以建的是大堆，这里建堆采用向下调整建堆，代码如下：

//向下建堆
//n -- 堆总大小
//father -- 当前堆中最后一个元素的父节点
void AdjustDwon(Heap* hp, int n, int father)
{
	int child = (father * 2) + 1;
	while (child < n)
	{
		//判断右孩子是否存在，且右孩子小于左孩子
		if (child + 1 < n && hp->data[child + 1] > hp->data[child])
		{
			child++;
		}
		if (hp->data[father] >= hp->data[child])
		{
			break;
		}
		else
		{
			Swap(&hp->data[father], &hp->data[child]);
			father = child;
		}
		child = (father * 2) + 1;
	}
}

// 堆的构建
void HeapCreate(Heap* hp, int* a, int n)
{
	assert(hp);
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (!tmp)
	{
		perror("malloc()");
		exit(-1);
	}
	hp->data = tmp;
	hp->capacity = hp->size = n;
	memcpy(hp->data, a, n * sizeof(int));
	//向下建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDwon(hp, hp->size, i);
	}
}

建堆图示：

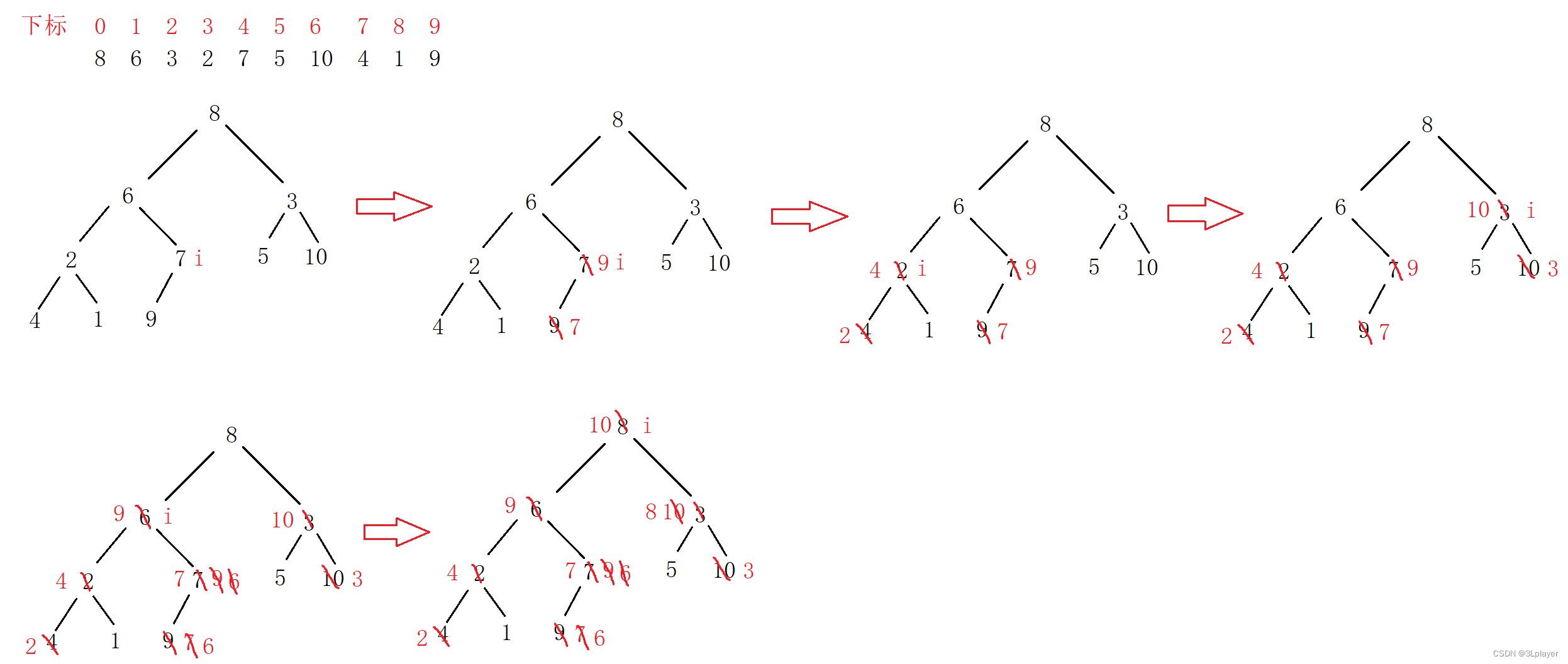
建好堆之后，就把堆顶的元素与堆中的最后一个元素交换，此时堆的总个数减一，剩下的元素再进行建大堆，最后再重复之前的步骤即可。

代码如下：

// 堆排序
void HeapSort(int* a, int n)
{
	Heap heap;
	//建堆
	HeapCreate(&heap, a, n);
	int tmp = n;
	for (int i = tmp; i > 0;)
	{
		Swap(&heap.data[0], &heap.data[i - 1]);
		i--;
		AdjustDwon(&heap, i, 0);
	}
}

七、快速排序

快速排序大体思想是，先定义好一个

key

，

key

的作用是用来分割两段区间，如果排的是升序，那么

key

的左边的数据都是比其小的，

key

的右边都是比其大的，

key

的选择一般是数组中最左边的值或者是最右边的值，这里选最左边的值做

key

，如果选最左边的值做

key

，此时定义两个变量

left

和

right

，

left = begin

，

right = end – 1

（数组中最后一个元素），那么一开始就要

right

先走，反之，

right

先走，遇到比

key

小的值时停下，然后

left

开始走，遇到比

key

大的值时停下，然后交换两值，再继续走，直到

left >= right

时结束，然后此时再让

key

和

left

或者

right

的值交换，此时的

key

就到了合适正确的位置，而

key

也分割出了两段区间，再对这两段区间进行上述的重复操作，最后就排好序了。

递归

hoare版本

图示（单趟）：





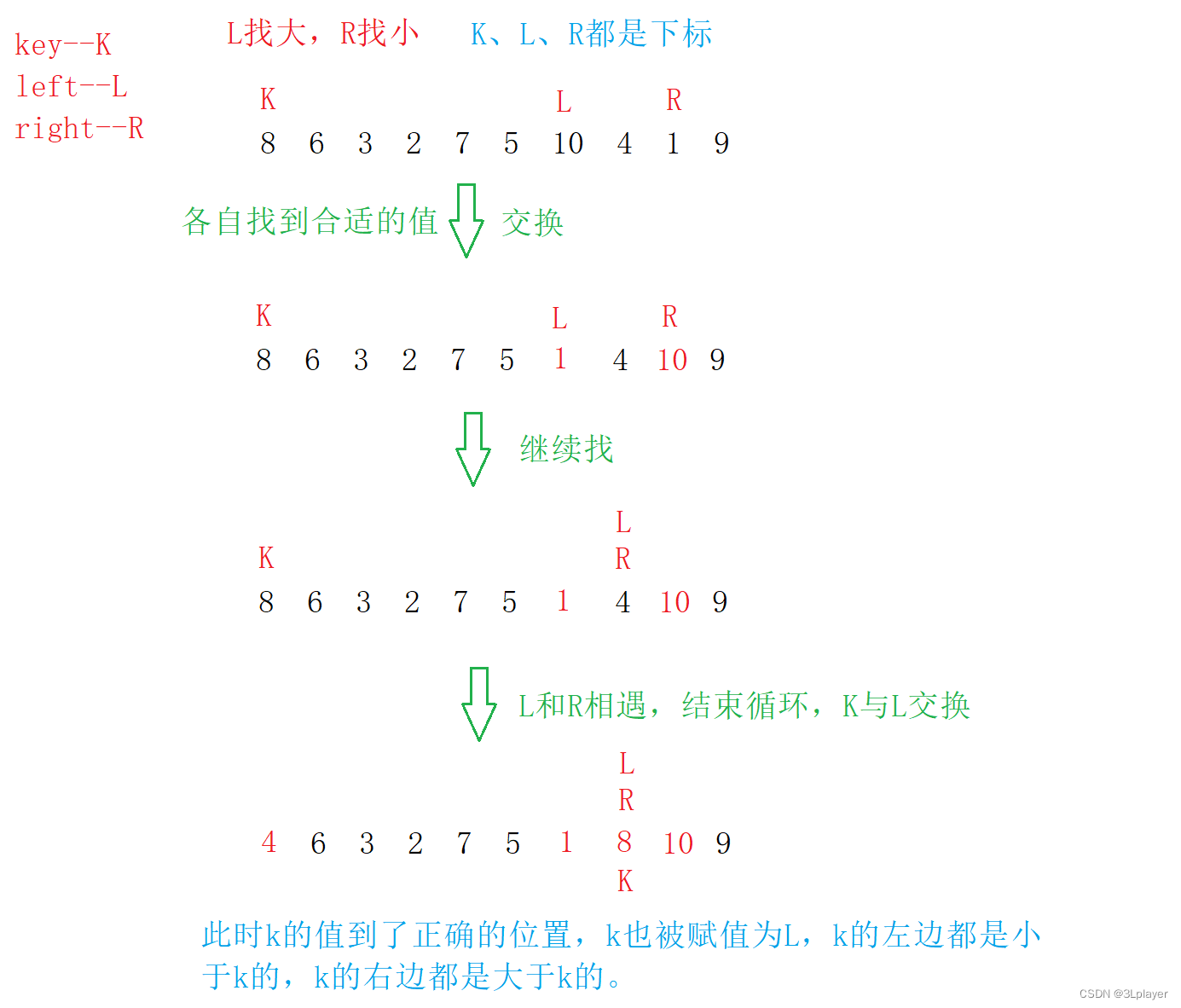
代码如下：

//交换
void Swap(int* e1, int* e2)
{
	int tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{
	int begin = left;
	int end = right;
	//三数取中优化
	int mid = GetMid(a, begin, end);
	Swap(&a[mid], &a[left]);
	int keyi = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi])
			right--;
		while (left < right && a[left] <= a[keyi])
			left++;
		Swap(&a[left], &a[right]);
	}
	Swap(&a[left], &a[keyi]);
	keyi = left;
	return keyi;
}

//快速排序
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	//小区间优化——大幅减少递归次数，大幅减少开辟的栈帧，预防栈溢出
	//到后面的层数运用直接插入排序
	if ((right - left + 1) <= 10)
	{
		//因为每次直接插入排序的起点都一定是0，所以加上left
		//因为left到right为闭区间，所以元素个数要加上1
		InsertSort(a + left, (right - left + 1));
	}
	else
	{
		int keyi = PartSort1(a, left, right);
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
}

挖坑法

图示（单趟）：





代码如下：

//交换
void Swap(int* e1, int* e2)
{
	int tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{
	int begin = left;
	int end = right;
	//三数取中优化
	int mid = GetMid(a, begin, end);
	Swap(&a[mid], &a[left]);
	int keyi = left;
	//坑位
	int hole = left;
	while (begin < end)
	{
		while (left < right && a[right] >= a[keyi])
			right--;
		Swap(&a[hole], &a[right]);
		hole = right;
		while (left < right && a[left] <= a[keyi])
			left++;
		Swap(&a[hole], &a[left]);
		hole = left;
	}
	Swap(&a[hole], &a[left]);
	return hole;
}

//快速排序
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	//小区间优化——大幅减少递归次数，大幅减少开辟的栈帧，预防栈溢出
	//到后面的层数运用直接插入排序
	if ((right - left + 1) <= 10)
	{
		//因为每次直接插入排序的起点都一定是0，所以加上left
		//因为left到right为闭区间，所以元素个数要加上1
		InsertSort(a + left, (right - left + 1));
	}
	else
	{
		int keyi = PartSort2(a, left, right);
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
}

前后指针法

前后指针法与前两种有一点区别，还是最左边做

key

，然后定义

prev

等于

begin

，

cur

等于

begin+1

，当

cur

的值小于

key

时，必须先

prev++

，再交换

prev

和

cur

的值，然后当

cur

的值大于等于

key

时，只让

cur++

即可，最后当

cur >= n

（元素个数）时结束循环。

图示（单趟）：





代码如下：

//交换
void Swap(int* e1, int* e2)
{
	int tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{
	//三数取中优化
	int mid = GetMid(a, left, right);
	Swap(&a[mid], &a[left]);
	int prev = left;
	int cur = left + 1;
	int keyi = left;
	while (cur <= right)
	{
		//找到比a[keyi]小的数，且仅当prev不等于cur时进行交换，因为当prev等于cur时交换同一个数没有意义
		if (a[cur] < a[keyi] && ++prev != cur)
			Swap(&a[prev], &a[cur]);
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	keyi = prev;
	return keyi;
}

//快速排序
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	//小区间优化——大幅减少递归次数，大幅减少开辟的栈帧，预防栈溢出
	//到后面的层数运用直接插入排序
	if ((right - left + 1) <= 10)
	{
		//因为每次直接插入排序的起点都一定是0，所以加上left
		//因为left到right为闭区间，所以元素个数要加上1
		InsertSort(a + left, (right - left + 1));
	}
	else
	{
		int keyi = PartSort3(a, left, right);
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
}

优化：

当前写的快速排序面对两个问题：

• 元素有序或趋于有序的情况下，这样
  
  left
  
  找大、
  
  right
  
  找小时会一骑绝尘，就是停不下来了，可能一直走到头都找不到，或者要走到很后面才找到，这样效率不高，所以第一个优化就是三数取中，分别取当前数据的
  
  begin
  
  、
  
  end
  
  、和
  
  mid
  
  位置的数，取三个数中的中间数做
  
  key
  
  ，这样即使有序或趋于有序也不会出现最坏的情况。
• 因为之前实现的快速排序是递归实现的，所以当元素个数很大时，会产生很深的递归，势必会开辟很多的栈帧，最终导致栈溢出，而快速排序的大部分递归都在后面的几层，所以我们设置当
  
  (right – left + 1) <= 10
  
  时就不再递归了，这里
  
  +1
  
  是因为传参传的是闭区间，开区间不需要
  
  +1
  
  ，当满足条件时，调用插入排序，效率会高些。

优化代码如下：

1）三数取中：

// 快速排序优化——三数取中（规避快排最坏情况，即待排序的数组有序）
// 三数取中即取既不是最大也不是最小的三个数的中间的那一个
int GetMid(int* a, int begin, int end)
{
	//快排——当数据中有大量的重复元素
	//int mid = begin + rand() % (end - begin);
	//正常情况
	int mid = begin + (end - begin) / 2;
	if (a[begin] > a[mid])
	{
		//begin最大，end最小
		if (a[mid] > a[end])
			return mid;
		//end最大，mid最小
		else if (a[end] > a[begin])
			return begin;
		//begin最大，mid最小
		else
			return end;
	}
	//a[mid] >= a[begin]
	else
	{
		//mid最大，end最小
		if (a[begin] > a[end])
			return begin;
		//end最大，begin最小
		else if (a[end] > a[mid])
			return mid;
		//min最大，begin最小
		else
			return end;
	}
}

2）小区间优化

//小区间优化——大幅减少递归次数，大幅减少开辟的栈帧，预防栈溢出
	//到后面的层数运用直接插入排序
	if ((right - left + 1) <= 10)
	{
		//因为每次直接插入排序的起点都一定是0，所以加上left
		//因为left到right为闭区间，所以元素个数要加上1
		InsertSort(a + left, (right - left + 1));
	}

非递归

快速排序的非递归实现需要借助栈这个数据结构的帮助，先把当前的

begin

和

end

入栈，然后第一趟排好后，

key

到了合适的位置，用

key

的下标来分割左右两段区间，分别是左边

[begin，key-1]

，右边

[key+1，end]

，将其分别入栈，每次取栈顶的两个元素来决定此次排序的区间，直至栈为空结束。（

注意栈是先入后出，入栈需注意！

）

栈的代码：

1）头文件

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>

// 支持动态增长的栈

//便于后续栈数据类型的修改
typedef int STDataType;

typedef struct Stack
{
	STDataType* data; //本体
	int top;	   // 栈顶
	int capacity;  // 容量 
}Stack;

// 初始化栈 
void StackInit(Stack* ps);
// 入栈 
void StackPush(Stack* ps, STDataType data);
// 出栈 
void StackPop(Stack* ps);
// 获取栈顶元素 
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数 
int StackSize(Stack* ps);
// 检测栈是否为空
bool StackEmpty(Stack* ps);
// 销毁栈 
void StackDestroy(Stack* ps);

2）源文件

#define _CRT_SECURE_NO_WARNINGS 1
#include"newstack.h"

// 初始化栈 
void StackInit(Stack* ps)
{
	assert(ps);
	STDataType* tmp = (STDataType*)malloc(sizeof(STDataType) * 5);
	if (!tmp)
	{
		perror("malloc()");
		exit(-1);
	}
	ps->data = tmp;
	ps->capacity = 5; 
	ps->top = 0; //top指向栈顶的上一个
}

// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	//空间满了，扩容
	if (ps->top == ps->capacity)
	{
		STDataType* tmp = (STDataType*)realloc(ps->data, sizeof(STDataType) * ps->capacity + 5);
		if (!tmp)
		{
			perror("realloc()");
			exit(-1);
		}
		ps->data = tmp;
		ps->capacity += 5;
	}
	//空间没满，正常入栈
	ps->data[ps->top++] = data;
}

// 出栈 
void StackPop(Stack* ps)
{
	assert(ps);
	assert(ps->top);
	ps->top--;
}

// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(ps);
	assert(ps->top);
	return ps->data[ps->top - 1];
}

// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->top;
}

// 检测栈是否为空
bool StackEmpty(Stack* ps)
{
	assert(ps);
	return ps->top == 0;
}

// 销毁栈 
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->data);
	ps->data = NULL;
	ps->capacity = ps->top = 0;
}

快速排序非递归代码如下：

// 快速排序 非递归实现
// 用栈实现
void QuickSortNonR(int* a, int left, int right)
{
	//创建栈
	Stack stack;
	//初始化栈
	StackInit(&stack);

	//先入最开始的区间下标
	//先入右边的，再入左边的，则出栈时top的数据为begin
	StackPush(&stack, right);
	StackPush(&stack, left);

	//直到栈为空时不存在区间则结束
	while (!StackEmpty(&stack))
	{
		int begin = StackTop(&stack);
		StackPop(&stack);
		int end = StackTop(&stack);
		StackPop(&stack);

		int keyi = PartSort3(a, begin, end);

		//判断区间内是否有至少两个值
		if (keyi + 1 < end)
		{
			//栈先入后出
			//先入end再入begin
			StackPush(&stack, end);
			StackPush(&stack, keyi + 1);
		}
		//判断区间内是否有至少两个值
		if (begin < keyi - 1)
		{
			//栈先入后出
			//先入end再入begin
			StackPush(&stack, keyi - 1);
			StackPush(&stack, begin);
		}
	}
	//销毁栈
	StackDestroy(&stack);
}

总结

至此，本章结束，谢谢观看！