背包问题身为一个非常经典的
动态规划
问题,理清思路很重要,在经过多次观看y总视频和b站解析,加上CSDN的文章辅助,我终于从很多不理解到大彻大悟,下面是我对于背包问题思路的总结,有问题的话欢迎指出。
谈到背包问题,先以下面这最经典的一道背包问题为例子
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第
i
i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
不废话,直接给出两种思路(可以结合看)
-
bilibili表格法
b站中把背包问题转化为一个表格来理解,我觉得特别有用,对于背包问题光是靠说是很难理解的,通过表格总结公式和方法,
对于该题非常有效,入门背包问题必须要看看。
(链接:【【动态规划】背包问题】
https://www.bilibili.com/video/BV1K4411X766/?share_source=copy_web&vd_source=7e63f1b6fa68c511b241d12721f0a4bc
)
先从一个具体例子入手

对于所给定的背包容量和物品状态,我们需要找出价值最大的一个组合,通过画图
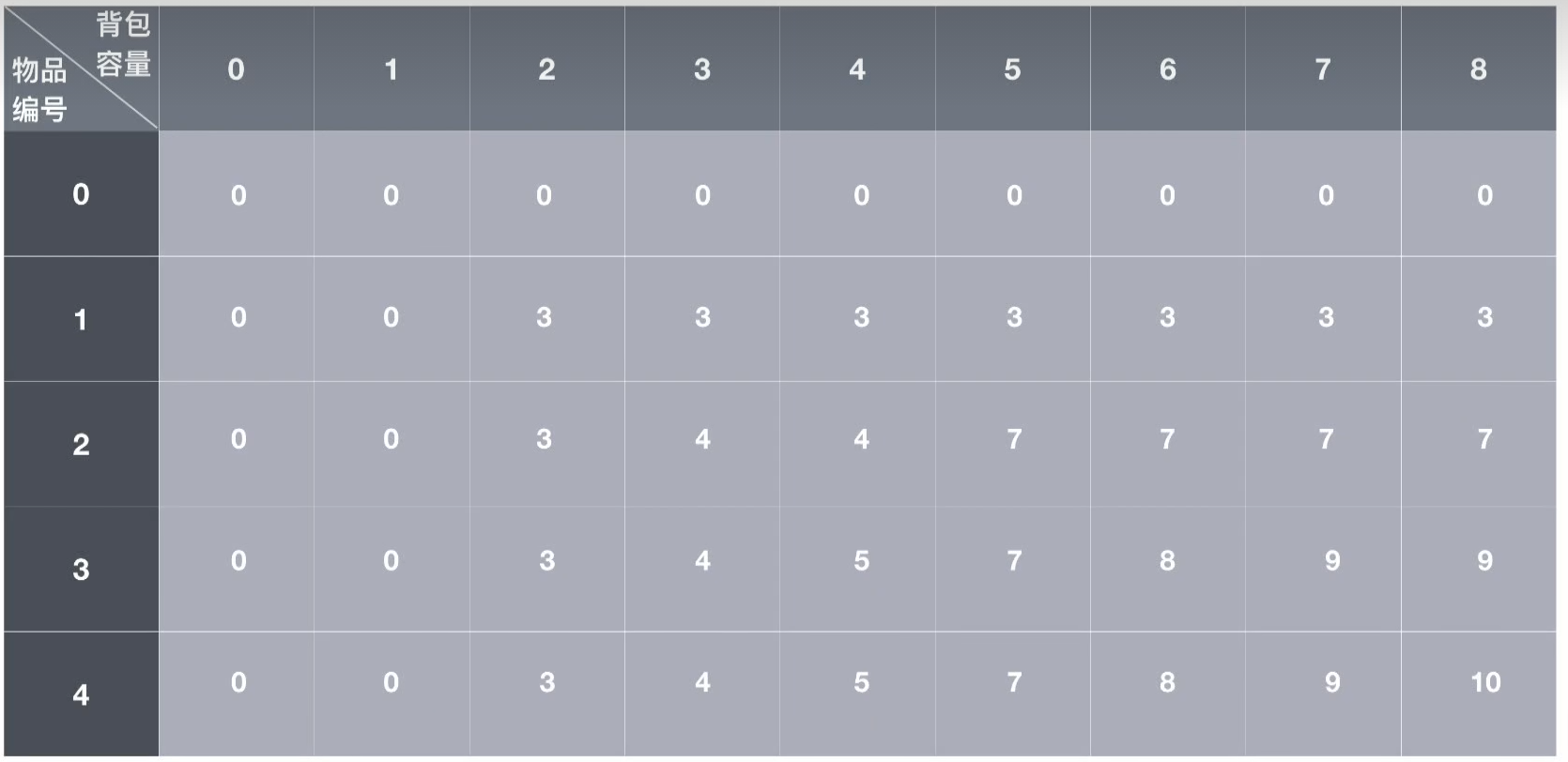
假设这是一个f(i,j)的数组,则
每一个f(i,j)的值都是前i(物品编号)件物品中,不超过j(背包容量)体积下的最大值
注意:
重中之重
,
每个格子是只考虑前i件物品
当时我比较不能理解的是为什么只考虑前i件物品下不超过该体积的值,编号i之后的物品不也可以放入该体积容量,假如该方法价值更高,那不是就不是该背包体积下最大价值了。
当时就是不能理解啊,后面思考之后终于悟了,
表格是所有情况都能考虑到,因为每个格子是在选了和不选的情况下取的最大值,我们只要只考虑前i件物品,后面每一个格子就能由前面的推出来,也能得到一个公式。
比如这题假如我们要算第f(4,8)的值,也就是该条件的最大价值,假设我们不知道该值,前面的数据我们都是知道的,
因此第4件物品有选和不选两种情况,
如果不选
,f(4,8)=f(3,8),本来需要考虑前4个,现在只需要考虑前3个,而f(3,8)前面是已经算出来了。
假如选
,则需要满足一个条件,即此时背包剩余的容量一定大于第四件物品体积,在此前提下,我们选了第4件物品,然后往前找,选了4之后我们表格应该找到f(3,8-第四件物品体积)也就是f(3,3),此时只考虑前3个物品,即f(4,8)=第四件物品价值+f(3,3),因为前面的f都是已经计算出来对应条件的价值最大值了,f(4,8)的值也就出来了。
最后,在选和不选中取一个最大值即使f(4,8)的值。
用表格容易理解,但确定是该方法不容易运用到其他同题型中,下面给出第二种
2.
闫式DP分析法
此方法比较有规律和逻辑,但对于新手不容易理解(nnd当时我看了好多遍才懂),但是第一种懂了,第二种也应该学习,因为该方法会了之后同题型就变得很简单了,后面我也会发类似题目的博客,用该方法来做,会发现简单很多。
大致思路与第一种是差不多的,也是把f(i,j)分为两种情况,这里不多做解释,和第一种同理
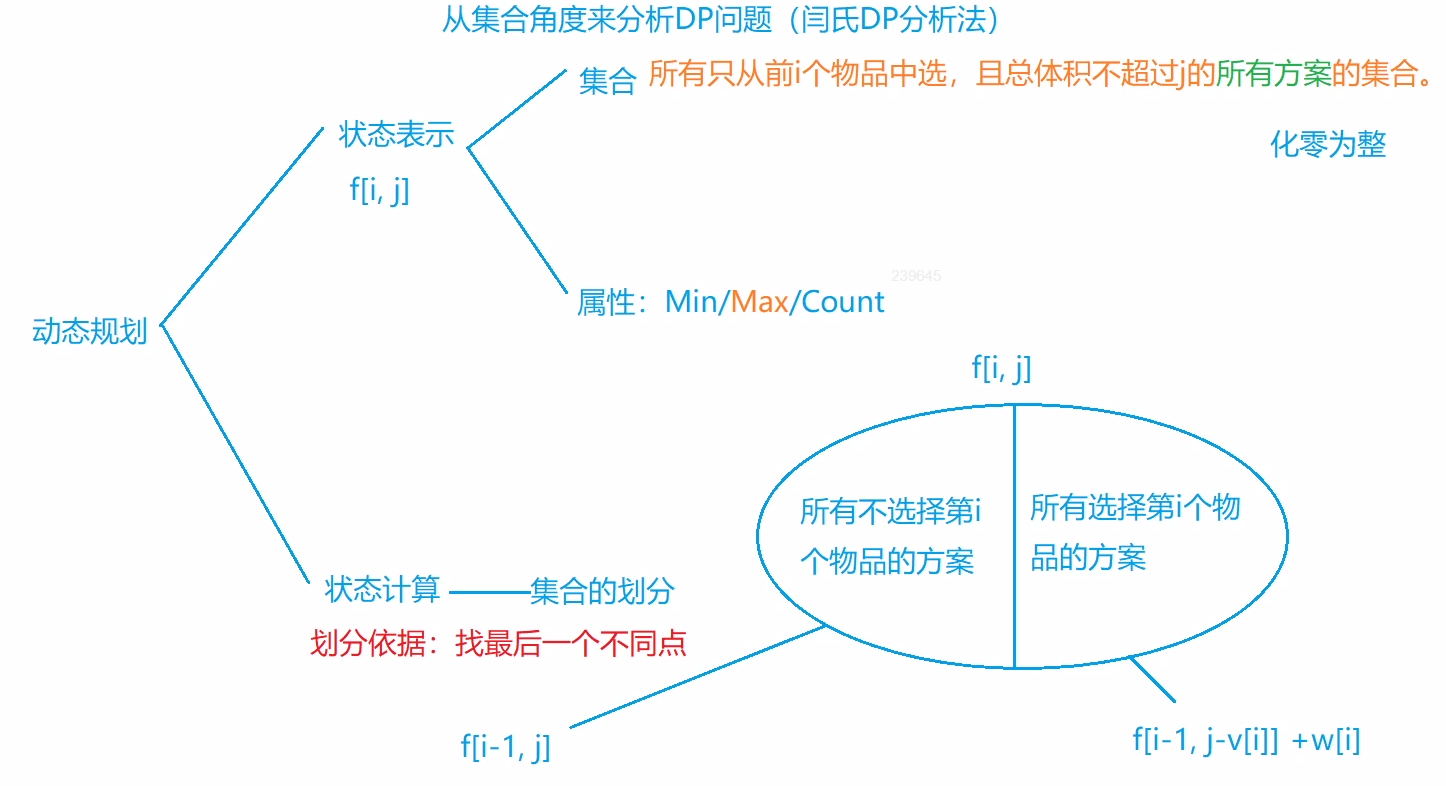
该方法很系统的对于该类题型的做题方法做了一个总结,此时f(i,j)为一个集合,每个f(i,j)的内容需要其属性来判断,背包问题要求我们找最大值,即属性为max,因此f(i,j)为对应条件下的最大值,然后进行状态计算,如何计算f(i,j),找到最后一个不同点进行划分,对于其他题型我们只需要对f(i,j)进行不同情况的划分考虑完就可以了。
状态计算的核心:
如何将现有的集合划分为更小的子集,使得所有子集都可以计算出来
,这是我们需要做的事
说了这么多,没有代码就是空谈
代码如下:(第一种和第二种方法都一样代码)
#include<iostream>
using namespace std;
const int N=1010;
int f[N][N];
int v[N],w[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)//i代表物品,第一件开始考虑
for(int j=0;j<=m;j++)//j代表背包容量,可以为0(一件都不选),因此从0开始
{
f[i][j]=f[i-1][j];//不选第i个物品
if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);//选第i个物品
}
cout<<f[n][m]<<endl;
return 0;
}
对于该代码我们是可以进行优化的,把二维转化为一维可以节省空间和时间,这里也给出优化后的代码,想要了解为什么的这里也给出一个链接
https://www.acwing.com/solution/content/1374/
,里面解释的非常好,这里我就不多阐明
优化后的代码:
#include<iostream>
using namespace std;
const int N=1010;
int f[N];
int v[N],w[N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
for(int j=m;j>=v[i];j--)//这里为什么从后往前遍历,因为为了防止第i层前面先被更新
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
cout<<f[m]<<endl;
return 0;
}最后祝大家早日理解背包问题,把动态规划用的行云流水,以后也会常更新dp的!!!