数据结构和算法(八)之哈希表理论
哈希表是一种非常重要的数据结构,在这一章中,我们通过实现来理解哈希表背后的原理和它的优势
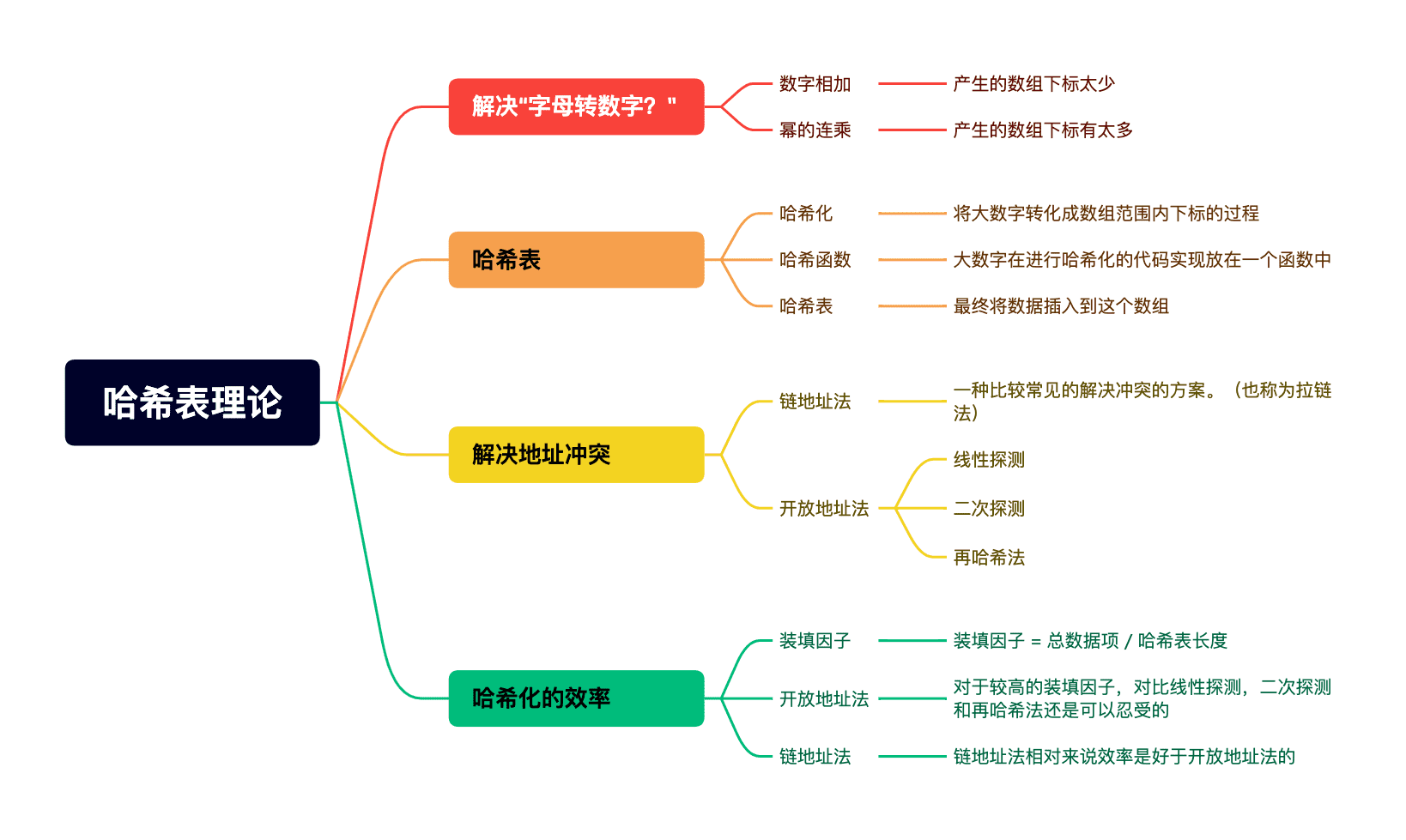
一. 认识哈希表
哈希表介绍
- 哈希表是一种非常重要的数据结构,几乎所有的编程语言都有直接或者间接的应用这种数据结构。
-
哈希表通常是基于数组进行实现的,但是相对于数组,他也很多的优势:
- 他可以提供非常快速的插入 —删除—查找操作
-
无论多少数据,插入和删除值需要接近常量的时间:即
O(1)
的时间级。实际上,只需要几个机器指令即可 - 哈希表的速度比数还要快,基本可以瞬间查找到想要的元素
- 哈希表相对于数来说编码要容易很多。
-
哈希表相对于数组的一些不足:
- 哈希表中的数据是没有顺序的,所以不能以一种固定的方式(比如从小到大)来遍历其中的元素。
-
通常情况下,哈希表中的
key
是不允许重复的,不能防止相同的
key
,用于保存不同的元素
-
那么,哈希表到底是什么呢?
- 似乎还是,没有说他到底是什么。
- 这也是哈希表不好理解的地方,不像数组和链表,甚至是树一样直接画出来你就知道他的结构,甚至是原理了。
-
他的结构就是数组,但是他神奇的地方在于对于下标值得一种变换,这种变换我们可以称之为哈希函数,通过哈希函数可以获得到
HashCode
体会哈希表
-
案例一:公司使用一种数据结构来保存所有员工
-
案例介绍:
- 假如一家公司有1000个员工,现在我们需要将这些员工的信息使用某种数据结构来保存起来
- 你会采用什么数据结构呢?
-
方案一:数组
- 一种方案是按照顺序将所有的员工依次存入一个长度为 1000 的数组中。每个员工的信息都保存在数组的某个位置上。
- 但是我们要查看某个具体员工的信息怎么办呢?一个个找吗?不太好找。
- 数组最大的优势是什么?通过下标值去获取信息。
- 所以为了可以通过数组快速定位到某个员工,最好给员工信息中添加一个员工编号,而编号对应的就是员工的下标值。
- 当查找某个员工的信息时,通过员工编号可以快速定位到员工的信息位置。
-
方案二:链表
- 链表对应插入和删除数据有一定的优势。
- 但是对于获取员工的信息,每次都必须从头遍历到尾,这种方式显然不是特别适合我们这里。
-
最终方案:
- 这样看最终方案似乎就是数组了。但是数组还是有缺点,什么缺点呢?
- 假如我想查看一下张三这位员工的信息,但是我不知道张三的员工都是问一下这个员工的编号,你怎么办呢?
- 当然,你说我可以问他。但是你每查找一个员工都是问一下这个员工的编号吗?不合适。
- 能不能有一种办法,让张三的名字和它的员工编号产生直接的关系呢?
- 也就是通过张三这个名字,我就能获取到它的索引值,而再通过索引值我就能获取到张三的信息呢?
-
这样的方案已经存在了,就是使用哈希函数,让某个
key
的信息和索引值对应起来。
-
案例介绍:
-
案例二:设计一个数据结构,保存联系人和电话。
-
方案一:数组
- 使用数组来存储联系人和电话不是非常合适。
- 因为如果要查询某个联系人,就需要从数组中一个个取出数组和查询的联系人比较。效率非常的低。
-
方案二:链表?
- 链表和数组一样,效率非常低。
-
方案三:有没有一种方案,可以将联系人和数组的下标值对应呢?
- 那么我们就可以让联系人的名字作为下标值,来获取这个联系人对应的电话。
- 但是联系人的名字(字符串)可以作为下标值吗?当然不可以。
- 所以你需要一种方案将字符串转成下标值。
-
方案一:数组
-
案例三:使用一种数据结构存储单词信息,比如有 50000 个单词。找到单词后每个单词有自己的翻译 & 读音 & 应用等等
-
方案一:数组?
- 这个案例更加明显能感觉到数组的缺陷。
-
我拿到一个单词
Python
,我想知道这个单词的翻译/读音/应用。怎么可以从数组中查到这个单词的位置呢? - 线性查找?50000次比较?
- 如果你使用数组来实现这个功能,效率会非常低,而且你一定没有学习过数据结构。
-
方案二:链表?
- 不需要考虑了吧?
-
方案三:有没有一种方案,可以将单词转成数组的下标值呢?
- 如果单词转成数组的下标,那么以后我们要查找某个单词的信息,直接按照下标值一步一步即可访问到想要的元素。
-
方案一:数组?
-
案例四:高级语言的编译器
- 事实上哈希表还有另外一个非常重要的应用场景,就是高级语言的编译器。
- 它通常用哈希表来保留符号表。
- 符号表记录了程序员声明的所有变量和函数名,以及它们在内存中的地址。
- 程序需要快速的访问这些名字,所以哈希表是理想的实现方式。
字母转数字
-
但是,怎样才能将一个字母转成数组的下标值呢?
- 单词转下表值,其实就是字母转数字,怎么转?
-
现在我们需要设计一种方案,可以将单词转成适当的下标:
- 其实计算机中有很多的编码方案就是用数字代替单词的字符。
-
比如
ASCll
编码:
a
是
97
,
b
是
98
,依次类推
122
代表
z
. -
我们也可以设计一个自己的编码系统,比如
a
是
1
,
b
是
2
,
c
是
3
,依次类推,
z
是
26
。当然我们可以加上空格用
0
代替,就是27个字符(不考虑大小写问题) - 但是,有了编码系统后,一个单词如何转成数字呢?
-
方案一:数字相加
-
一个装换单词的简单方案就是把单词每个字符的编码求和。
-
例如单词
cats
转成数字:
3+1+20+19=43
,那么
43
就作为
cats
单词的下标存在数组中。 -
问题:按照这种方案有一个很明显的问题就是很多单词最终的下标可能都是
43
。-
比如
was/tin/give/tend/moan
等等 - 我们知道数组中一个下标值位置只能存储一个数据,如果存入后来的数据,必然会造成数据的覆盖。
- 一个下标存储这么多单词显然是不合理的。
-
比如
-
-
方案二:幂的连乘
-
现在,我们想通过一种算法,让
cats
转成数字后不那么普通。数字相加的方案就有些过于普通了。 - 有一种方案就是使用幂的连乘,什么是幂的连乘呢?
-
其实我们平时使用的大于
10
的数字,可以用一种幂的连乘来表示他的唯一性:比如:
7654=
7
∗
1
0
3
+
6
∗
1
0
2
+
5
∗
10
+
4
7654 = 7*10^3+6*10^2+5*10+4
7
6
5
4
=
7
∗
1
0
3
+
6
∗
1
0
2
+
5
∗
1
0
+
4
-
我们的单词也可以使用这种方案来表示:比如
ca
t
s
=
3
∗
2
7
3
+
1
∗
2
7
2
+
20
∗
27
+
17
=
60337
cats=3*27^3+1*27^2+20*27+17=60337
c
a
t
s
=
3
∗
2
7
3
+
1
∗
2
7
2
+
2
0
∗
2
7
+
1
7
=
6
0
3
3
7
- 这样得到的数字可以几乎保证他的唯一性,不会和别的单词重复。
-
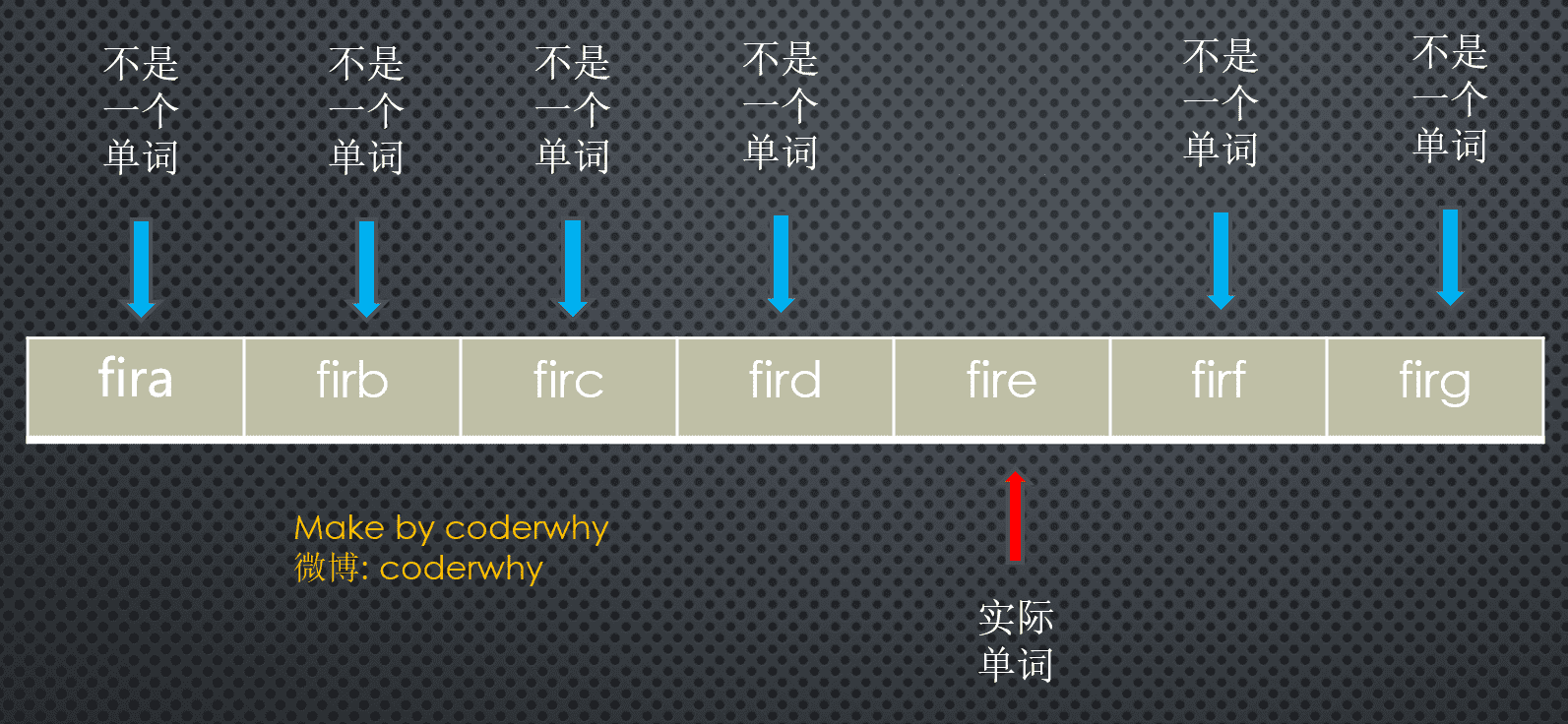
问题:如果一个单词是
zzzzzzzzzz
(一般英文单词不会超过10个字符)。那么得到的数字超过
7000000000000
.数组可以表示这么大的下标值吗? - 而且就算能创建这么大的数组,事实上有很多是无效的单词。创建这么大的数组是没有意义的。
-
现在,我们想通过一种算法,让
-
两种方案总结:
- 第一种方案(把数字相加求和)产生的数组下标太少。
- 第二种方案(与27的幂相乘求和)产生的数组下标有太多。
认识哈希化
- 现在需要一种压缩方法,吧幂的连乘方案系统中得到的巨大整数范围压缩到可接受的数组范围中。
-
对于英文词典,多大的数组才合适呢?
-
如果只有
50000
个单词,可能会定义一个长度为
50000
的数组。 -
但是实际情况中,往往需要更大的空间来存储这些单词。因为我们不能保证单词会映射到每一个位置。(比如两倍的大小:
100000
).
-
如果只有
-
如何压缩呢?
-
现在,就找一种方法,吧
0
到超过
7000000000000
的范围,压缩到
100000
。 - 有一种简单的方法就是使用取余操作符,他的作用得到一个数被另外一个数整除后的余数
-
现在,就找一种方法,吧
-
取余操作的实现:
- 为了看到这个方法如何工作,我们先来看一个小点的数字范围压缩到一个小点的空间中。
-
假如把从
0~199
的数字,使用
largeNumber
代表,压缩为从
0
到
9
的数字,比如使用
smallRange
代表。 -
下标值得结果:
index = largeNumber % smallRange
; -
当一个数被
10
整除时,余数一定在
0~9
之间; -
比如
13%10=3,157%10=7
-
当然,这中间还是会有重复,不过重复的数量明显变小了。因为我们的数组是
100000
,而只有
50000
个单词. -
就好比,你在
0~199
中间选取5个数字,放在这个长度为10 的数组中,也会重复,但是重复的概率非常小。(后面我们会讲到真的发生重复了应该怎么解决)
-
认识了上面的内容,相信你应该懂了哈希表的原理了,我们来看看几个概念:
-
哈希化
:将大数字转化成数组范围内下标的过程,我们就称之为哈希化 -
哈希函数
:通常我们会将单词转成大数字,大数字在进行哈希化的代码实现放在一个函数中,这个函数我们称为哈希函数。 -
哈希表
:最终将数据插入到这个数组,我们就称之为是一个哈希表。
-
二. 地址的冲突
尽管
50000
个单词,我们使用了
100000
个位置来存储,并且通过一种相对比较好的哈希函数来完成。但是依然有可能会发生冲突,比如
melioration
这个单词,通过哈希函数得到它数组的下标值后,发现那个位置上已经存在一个单词
demystify
,因为他经过哈希化后和
melioration
得到的下标是相同的这种情况我们称为冲突
什么是冲突?
-
前面我们已经简要说明了,什么是冲突。虽然我们不希望这种情况发生,当然更希望每个下标对应一个数据项,但是通常这是不可能的。

-
就像之前
0~199
的数字选取5个放在长度为10 的单元格中-
如果我们随机选出来的是
33,82,11,45,90
,那么最终它们的位置会是
3-2-1-5-0
,没有发生冲突。 -
但是如果其中有一个
33
,还有一个
73
呢?还是发生了冲突。
-
如果我们随机选出来的是
-
我们需要针对这种冲突提出一些解决方案,即使冲突的可能性比较小,你依然需要考虑到这种情况,以便发生的时候进行对应的处理代码。
-
如何解决这种冲突呢?常见的情况有两种方案。
-
链地址法
。 -
开放地址法
。
-
链地址法
-
链地址法是一种比较常见的解决冲突的方案。(也称为拉链法)
- 其实,如果你理解了为什么产生冲突,看到图后就可以立马理解链地址法是什么含义了。
-
链地址法图片

-
图片解析:
- 从图片中我们可以看出,链地址法解决冲突的方法是每一个数组单元中存储的不再是的单个数据,而是一个链条。
- 这个链条使用什么数据结构呢?常见的树数组或者链表。
- 比如是链表,也就是每个数组单元中存储着一个链表。一旦发现重复,将重复的元素插入到链表的首端或者末端即可。
- 当查询时,先根据哈希化后的下标值找到对应的位置,再取出链表,依次查询需要的数据。
-
数组还是链表呢?
- 数组或者链表在这里其实都可以,效率上差不多。
-
因为根据哈希化的
index
找出这个数组或者链表时,通常就会使用线性查找,这个时候数组和链表的效率是差不多的。 - 当然在某些实现中,会将新插入的数据放在数组或者链表的最前面,因为觉得新插入的数据用于取出的可能性更大。
- 这种情况下最好采用链表,因为数组在首位插入数据时需要所有其他项后移的,链表就没有这样的问题。
- 当然,我觉得对于这个也看业务需求,不见得新的数据就访问次数会更多:比如我们微信新添加的好友,可能是刚认识的,联系的频率不见得比我们的老朋友更多,甚至新加的只是聊一两句。
- 所以,这里个人觉得选择数据或者链表都是可以的。
开放地址法
-
开放地址法的主要工作方式是寻找空白的单元格来添加重复的数据。
-
我们还是通过图片来了解开放地址法的工作方式。

-
图片解析:
- 从图片的文字中我们可以了解到,开放地址法其实就是要寻找空白的位置来放置冲突的数据项。
-
但是探索这个位置的方式不同,有三种方法:
-
线性探测
-
二次探测
-
再哈希化
-
线性探测
- 线性探测非常好理解:线性的查找空白的单元。
-
插入
32
:-
经过哈希化得到的
index=2
,但是在插入的时候,发现该位置已经有了
82
,怎么办呢? -
线性探测就是从
index
位置 +1 开始一点点查找合适的位置来放置
32
,什么是合适的位置呢? -
空的位置就是合适的位置,在我们上面的例子中就是
index=3
的位置,这个时候
32
就会放在该位置。
-
经过哈希化得到的
-
查询
32
:-
查询
32
和插入
32
比较相似。 -
首先经过哈希化得到
index=2
,比如
2
的位置结果和查询的数值是否相同,相同那么就直接返回。 -
不相同呢?线性查找,从
index
位置 + 1开始查找和
32
一样的。 -
这里有一个特别需要注意的地方:如果
32
的位置我们之前没有插入,是否将整个哈希表查询一遍来确定
32
存不存在吗? -
当然不是,查询过程有一个约定,就是查询到空位置,就停止。(因为查询到这里有空位置,
32
之前不可能跳过空位置去其他的位置)
-
查询
-
删除
32
:- 删除操作和插入查询比较类似,但是也有一个特别注意点。
-
注意
:删除操作一个数据项时,不可以将这个位置下标的内容设置为
null
,为什么呢? -
因为将它设置为
null
可能会影响我们之后查询其他操作,所以通常删除一个位置的数据项时,我们可以将它进行特殊处理(比如设置为
-1
)。 -
当我们之后看到
-1
位置的数据项时,就知道查询时要继续查询,但是插入时这个位置可以防止数据。
-
线性探测的问题:
- 线性探测有一个比较严重的问题,就是聚集。什么是聚集呢?
-
比如我在没有任何数据的时候,插入的是
22-23-24-25-26
,那么意味着下标值:
2-3-4-5-6
的位置都有元素。这种一连串填充单元就叫做聚集。 - 聚集会影响哈希表的性能,无论是插入、查询、删除都会影响。
-
比如我们插入一个
32
,会发现连续的单元都不允许我们放置数据,并且再把这个过程中我们需要探索多次。 - 二次探测可以解决一部分这个问题,我们一起来看一看。
二次探测
-
我们刚才谈到,线性探测存在的问题:就是如果之前的数据是连续插入的,那么新插入的一个数据可能需要探测很长的距离。
-
二次探测在线性探测的基础上进行了优化:
- 二次探测主要优化的是探测时的步长,什么意思呢?
-
线性探测,我们可以看成是步长为
1
的探测,比如从下标值
x
开始,那么线性探测就是
x+1,x+2,x+3
依次探测。 -
二次探测,对比步长做了优化,比如从下标值
x
开始,
x+
1
2
x+1^2
x
+
1
2
,
x+
2
2
x+2^2
x
+
2
2
,
x+
3
2
x+3^2
x
+
3
2
- 这样就可以一次性探测比较长的距离,以避免哪些聚集带来的影响。
-
二次探测的问题:
-
比如我们连续插入的是
32-112-82-2-192
,那么他们依次累加的时候步长是相同的 - 也就是这种情况下会造成步长不一的一种聚集。还是会影响效率。
- 怎么根本解决这个问题呢?让每个人的步长不一样,一起来看看再哈希法吧。
-
比如我们连续插入的是
再哈希法
- 为了消除线性探测和二次探测中无论步长 +1 还是步长 + 平法中存在的问题,还有一种最常用的解决方案:再哈希法。
-
再哈希法:
- 二次探测的算法产生的探测序列步长是固定的:1,4,9,16,依次类推。
- 现在需要一种方法:产生一种依赖关键字的探测序列,而不是每个关键字都一样。
- 那么,不同的关键字即使映射到相同的数组下标,也可以使用不同的探测序列。
- 在哈希化的做法就是:把关键字用另外一个哈希函数,在做一次哈希化,用这次哈希化的结果作为步长。
- 对于指定的关键字,步长在整个探测中是不变的,不过不同的关键字使用不同的步长。
-
第二次哈希化需要具备如下特点:
- 和第一个哈希函数不同。(不要使用上一次的哈希函数了,不然结果还是原来的位置)
-
不能输出为
0
(否则,将没有步长。每次探测都是原地踏步,算法就进入了死循环)
-
其实,我们不用费脑细胞来设计了,计算机专家已经设计出一种工作很好的哈希函数:
-
stepSize = constant - (key - constant)
-
其中
constant
是质数,且小于数组的容量。 -
例如:
stepSize = 5 -(key % 5)
,满足需求,并且结果不可能为
0
-
三. 哈希化的效率
哈希表中执行插入和搜索操作可以达到
O(1)
的时间级,如果没有发生冲突,只需要使用依次哈希函数和数组的引用,就可以插入一个新数据项或找到一个已经存在的数据项。如果发生冲突,存取时间就依赖后来的探测长度。一个单独的查找或插入时间于探测的长度成正比,这里还要加上哈希函数的常量时间。
平均探测长度以及平均存取时间,取决于填装因子,随着填装因子变大,探测长度也越来越大。
随着填装因子变大,效率下降的情况,在不同开放地址法方案中比链地址法更严重,所以我们来对比一下他们的效率,再决定我们选取的方案。
装填因子
-
在分析效率之前,我们先了解一个概念:
装填因子
。 -
装填因子表示当前哈希表中已经包含的数据项和整个哈希白长度的比值。
-
装填因子 = 总数据项 / 哈希表长度
-
-
开放地址法的装填因子最大是多少呢?
1
,因为他必须寻找到空白的单元才能将元素放入。 -
链地址法的装填因子呢?可以大于
1
,因为拉链法可以无限的延伸下去,只要你愿意。(当然后面效率就变低了)
开放地址法
-
线性探测
-
下面的等式显示了线性探测时,探测序列
(P)
和装填因子
(L)
的关系-
对成功的查找:
P=
(
1
+
1
/
(
1
−
L
)
)
/
2
P=(1+1/(1-L))/2
P
=
(
1
+
1
/
(
1
−
L
)
)
/
2
-
对不成功的查找:
P=
(
1
+
1
/
(
1
−
L
)
2
)
/
2
P=(1+1/(1-L)^2)/2
P
=
(
1
+
1
/
(
1
−
L
)
2
)
/
2
-
对成功的查找:
-
公式来自于Knuth(算法分析领域的专家,现代计算机的先驱人物)
-
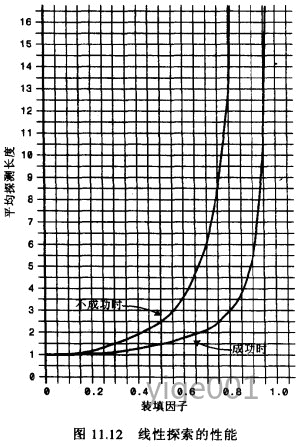
图解算法的效率:
-
图片解析:
-
当装填因子是
1/2
时,成功的搜索需要
1.5
次比较,不成功的搜索需要
2.5
次 -
当装填因子为
2/3
时,分别需要
2
次和
5
次比较 - 如果装填因子更大,比较次数会非常大。
-
应该使用装填因子保持在
2/3
以下,最好在
1/2
以下,另一方面,装填因子越低,对于给定数量的数据项,就需要越多的空间。 - 实际情况中,最好的装填因子取决于存储效率和速度之间的平衡,随着装填因子变小,存储效率下降,而速度上升。
-
当装填因子是
-
-
二次探测和再哈希法
-
二次探测和再哈希法的性能相当。他们的性能比线性探测略好。
-
对成功的搜索,公式是:
−l
o
g
2
(
1
−
l
o
a
d
F
a
c
t
o
r
)
/
l
o
a
d
F
a
c
t
o
r
-log2(1-loadFactor)/loadFactor
−
l
o
g
2
(
1
−
l
o
a
d
F
a
c
t
o
r
)
/
l
o
a
d
F
a
c
t
o
r
-
对于不成功的搜索,公式是:
1/
(
1
−
l
o
a
d
F
a
c
t
o
r
)
1/(1-loadFactor)
1
/
(
1
−
l
o
a
d
F
a
c
t
o
r
)
-
对成功的搜索,公式是:
-
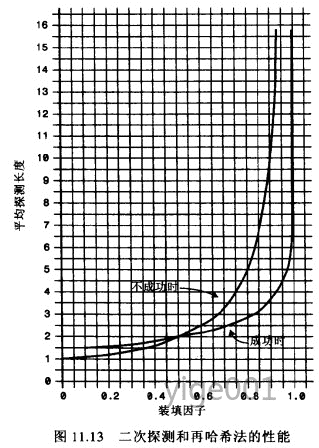
对应的图:
-
图片解析:
-
当装填因子是
0.5
时,成功和不成功的查找平均需要
2
次比较 -
当装填因子为
2/3
时,分别需要
2.37
和
3.0
次比较 -
当装填因子为
0.8
时,分别需要
2.9
和
5.0
次。 - 因此对于较高的装填因子,对比线性探测,二次探测和再哈希法还是可以忍受的。
-
当装填因子是
-
链地址法
-
链地址法的效率分析有些不同,一般来首比开放地址法简单。我们来分析一下这个公式应该是怎么样的。
-
假设哈希表包含
arraySize
个数据项,每个数据项有一个链表,在表中一共包含
N
个数据项。 -
那么,平均起来每个链表有多少个数据项呢?非常简单,
N/arraySize
。 - 有没有发现这个公式有点眼熟?其实就是装填因子。
-
假设哈希表包含
-
OK,那么我们现在就可以求出查找成功和不成功的次数了
-
成功可能只需要查找链表的一半即可:
1+
l
o
a
d
F
a
c
t
o
r
/
2
1+loadFactor/2
1
+
l
o
a
d
F
a
c
t
o
r
/
2
-
不成功呢?可能需要将整个链表查询完才知道不成功:
1+
l
o
a
d
F
a
c
t
o
r
1+loadFactor
1
+
l
o
a
d
F
a
c
t
o
r
-
成功可能只需要查找链表的一半即可:
-
对应的图
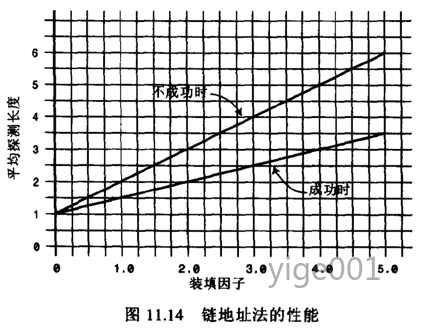
效率的结论
- 经过上面的比较我们可以发现,链地址法相对来说效率是好于开放地址法的
-
所以在真实开发中,使用链地址法的情况下较多,因为它不会因为添加某元素后性能急剧下降
-
比如在
Java
的
HashMap
中使用的就是链地址法。
-
比如在