1.

1.1题目分析:
1.1.1题干分析:
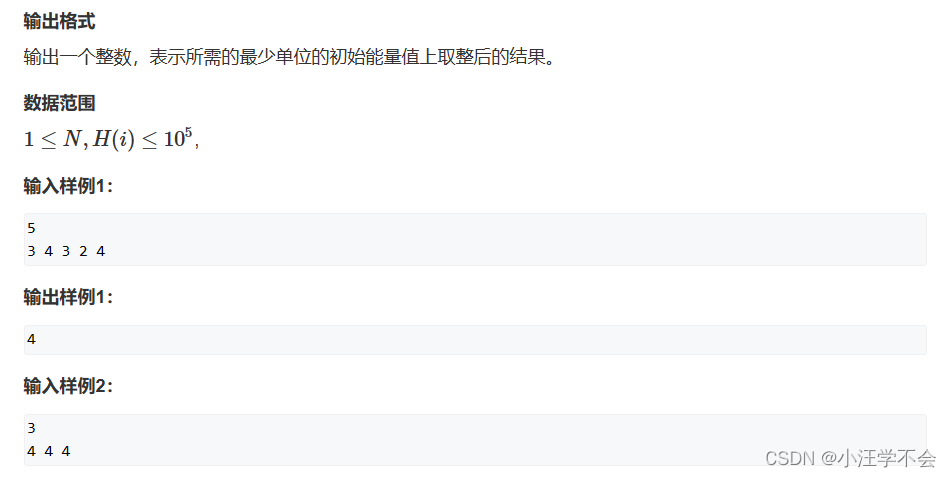
输出结果:能量E
输出范围:[1,1e5]
当h>E E = E – (h – E) = 2E – h
当h<=E E = E + E – h = 2E – h
无论h与E的大小关系,都有
E = 2E – h
1.1.2.方法选用分析:
求最大最小问题
,依次考虑
二分
、
dfs
、
Dp
、
贪心
二分要考虑结果是否有
二段性
和
单调性
二段性:
能量
E
= mid 时 , 能否使E保持大于零
单调性
:E_k成立时, E_k+1也成立
可以采用二分法解题
1.1.3.方法结题分析:
边界:L = 0 , R = 1e5
判断条件 :能量E能否跳过,即为E始终大于0
当E = mid 可以跳过 , 则最小值在左侧,所以
R=mid
,则
mid = (l+r)>> 1
当E = mid 不能跳过 , 则最小值在右侧,且最小值不是mid,则
L = mid +1

1.2程序设计:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010 ;
int n;
int h[N];
//判断E能否跳过
bool check(int e){
bool fleg = true ;
for(int i=1;i<=n;i++)
{
e = 2*e - h[i] ; //能量表达式
if(e>=1e5) { //能量大于边界,肯定能跳过。防止爆掉,break结束循环
fleg = true;
break;
}
if(e<0) { //能量跳不过
fleg=false;
break;
}
}
return fleg ;
}
int main(){
scanf("%d",&n); //读取楼个数
for(int i=1;i<=n;i++) scanf("%d",&h[i]); //读取楼高度
//二分法
int l =0 ,r= 1e5; //左右区间
while(l<r) //循环条件
{
int mid = (l+r)>>1; //二分
if(check(mid)) r = mid ; //判断条件
else l = mid + 1 ;
}
printf("%d\n",r); //输出结果
return 0;
}
2.

2.1题目分析:
2.1.1.题干分析:
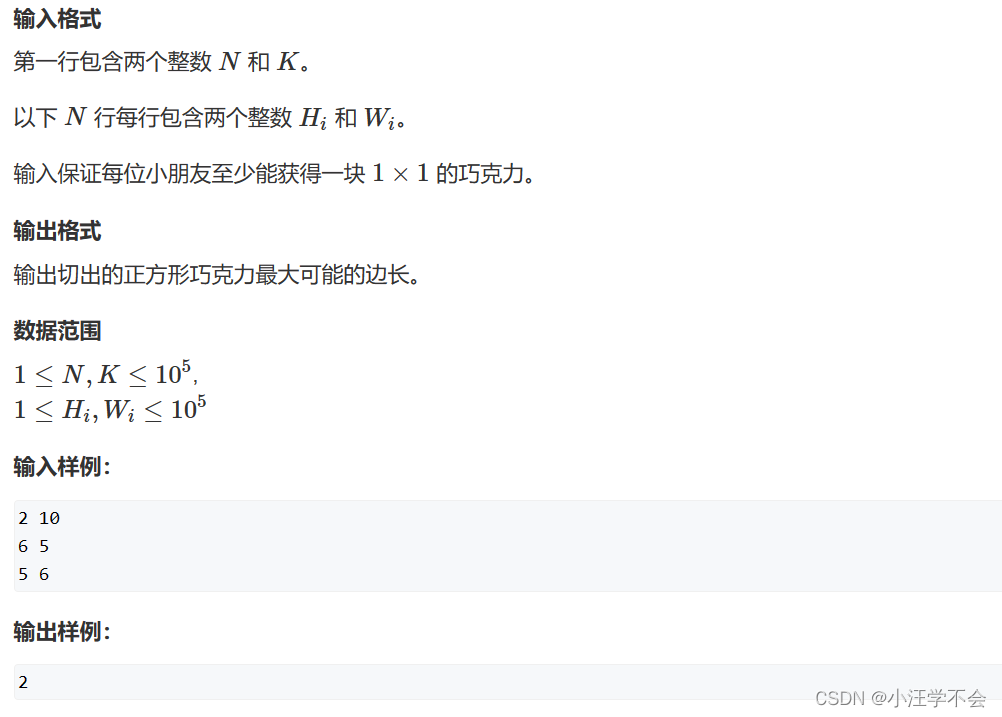
输出结果:切分正方形巧克力的边长
输出范围:[1,1e5]
分巧克力只能切割,不能拼接!!!
一块边长为H[i] 和 K[i] 的巧克力,分为边长为z的正方形,可分
( H[i] / z ) * ( K[i] / z )
块(向下取整)。
2.1.2.方法选用分析:
求最大最小问题
,依次考虑
二分
、
dfs
、
Dp
、
贪心
二分要考虑结果是否有
二段性
和
单调性
单调性
:边长为z的正方形成立时, z-1 的正方形也成立
二段性:
边长 z
= mid ,判断能否成立
可以采用二分法解题
2.1.3.方法结题分析:
边界:L = 1 (至少分成1 * 1的巧克力) , R = 1e5
判断条件 :按照边长为z的正方形切割得到的块数sum能否大于小朋友个数
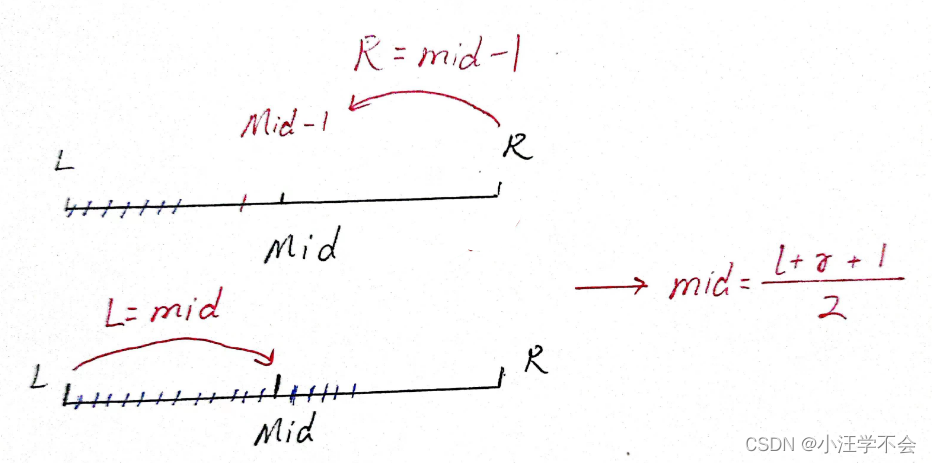
当 z = mid 成立 , 则最大值在右侧,所以
L
= mid
,则
mid =(l + r + 1 )>> 1
当 z = mid 不成立 , 则最大值在左侧,且最大值不是mid,则
R = mid -1
2.2.程序设计:
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 100010;
int n, f ; //n:巧克力个数 f:小朋友个数
int H[N], W[N] ; //巧克力边长H[N],W[N]
int z ; //正方形边长
bool check(int z)
{
int sum=0 ;
for(int i=0;i<n;i++)
{
sum = sum + ( H[i] / z ) * ( W[i] / z ) ; //分巧克力块数
if(sum >= f) return true; //足够分给f个小朋友
}
return false;
}
int main()
{
scanf("%d %d",&n,&f); //读取n块巧克力 ,f个小朋友
for(int i=0;i<n;i++) scanf("%d %d",&H[i],&W[i]); //n块巧克力的边长H和W
//二分
int mid;
int l = 1 , r = N ;
while(l < r)
{
mid = l + r + 1 >> 1;
if(check(mid)) l = mid ;
else r = mid - 1 ;
}
printf("%d\n",r);
return 0;
}
3.


3.1题目分析:
3.1.1.题干分析:

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdio>
using namespace std ;
const int N = 2500010;
struct Sum {
int s, c, d;
bool operator< (const Sum &t) const
{
if(s != t.s) return s < t.s;
if(c != t.s) return c < t.c;
return d < t.d;
}
}sum[N];
int n , m;
int main()
{
cin >> n ;
for(int c = 0; c*c <=n; c++){
for(int d=c; c*c + d*d <=n; d++)
sum[m ++] = {c*d + d*d,c,d};
}
sort(sum,sum + m); //排序
for(int a=0; a*a<=n ; a++){
for(int b=a; a*a + b*b <= n;b++)
{
int t = n - a*a - b*b ;
//二分
int l =0 ,r =m-1;
while(l<r)
{
int mid= l+r >> 1;
if(sum[mid].s >= t) r=mid;
else l = mid+1;
}
if(sum[l].s == t)
{
printf("%d %d %d %d\n", a, b, sum[l].c, sum[l].d);
return 0;
}
}
}
return 0;
}