博客

前言

与普通的二分查找不同，本周的题目基本都是运用到

二分法来找结果

的思路。我把这类题归类为

二分法猜结果

。

• 从小到大，我们经历无数多的数学题目，也掌握了一种方法：如果我们不知道这道题答案是什么时，我们可以猜一个答案套进去，如果符合题目，则答案正确。
• 在算法中，我们也可以用到这种思路。我们只要已知的区间，就能通过区间找到答案。
• 但假如区间是 int 类型，如果顺序查找的话，就得遍历 2^31 次，但如果用二分法，时间就降低到 31 次。

敲黑板：二分法猜结果大部分应用在求最值问题。

① 69. x 的平方根

https://leetcode-cn.com/problems/sqrtx/

这道题的思路可以用

二分法猜结果

来计算。因为满足条件：已知区间，求最值。

已知区间是 [1 ~ x]，且要求最接近 sqrt(x) 的整数。

• 先用二分法得到一个值，将其带入平方中，如果大于 x，则要减小，如果小于 x，则要增大。
• 但此题还要注意当x =
  
2^31-1

  时，如果求中位数，直接用
  
(left + right) / 2

  会造成溢出，所以要分解下式子为
  
left + (right-left) / 2

  。

class Solution {
    public int mySqrt(int x) {
        int left = 1, right = x;
        while(left <= right){
            int mid = left + (right-left) / 2;
            if((long)mid * mid == x)
                return mid;
            if((long)mid * mid < x)
                left = mid+1;
            else
                right = mid-1; 
        }
        return right;
    }
}

② 374. 猜数字大小

https://leetcode-cn.com/problems/guess-number-higher-or-lower/

此题也是二分法猜结果。思路跟上面一致。

public class Solution extends GuessGame {
    public int guessNumber(int n) {
        int left = 0, right = n;
        while(left < right){
            int mid = left + (right - left) / 2;
            if(guess(mid) == 0)
                return mid;
            if(guess(mid) == 1)
                left = mid + 1;
            else
                right = mid - 1; 
        }
        return right;
    }
}

④ 475. 供暖器

https://leetcode-cn.com/problems/heaters/

思路一：二分法猜结果

这道题对应题目第四道题，由于已知范围（整个地域的长度） 0 ~ max(房屋的最大位置，供暖器的最大位置），求最值，故可以用

二分法猜结果

来做。

• 从距离区间中得到中位数
• 用这个中位数进行判断：遍历供暖器，看当前的供暖范围能否覆盖到每一个房间，如果能覆盖每一个，则返回 true，否则返回 false。
• 根据判断中位数函数的返回结果来处理
  
  + 如果为 true，则结果值可以再小，二分法缩小区间
  
  + 如果为 false，则结果值要大一点，二分法缩小区间

时间复杂度：O(nlogn)，n 粗略为房屋的数量。

class Solution {
    int[] houses;
    int[] heaters;

    public int findRadius(int[] houses, int[] heaters) {
        Arrays.sort(houses);         // 房屋需要排序
        Arrays.sort(heaters);        // 供暖器需要排序
        this.houses = houses;        // 设为全局变量
        this.heaters = heaters;   

        int left = 0, right = Math.max(heaters[heaters.length-1], houses[houses.length-1]) - houses[0];  // 区间范围

        while (left < right){
            int mid = left + (right - left) / 2;
            if (checkＲadius(mid)){      // 判断这个中位数是否满足
                right = mid;             // 满足值要更小，不 -1 是由于这个值可能为最终结果
            }else{
                left = mid + 1;          // 满足值要更大，+1 是这个数确定不是结果了
            }
        }
        return right;
    }

    public boolean checkＲadius(int radius){     // 判断一个值能否满足结果
        int k = 0;
        for (int i=0; i < heaters.length; i++){
            while (k < houses.length && houses[k] >= heaters[i] - radius && houses[k] <= heaters[i] + radius){
                k++;         // 这个房屋能够被覆盖
            }
            if (k == houses.length)      // 全部房屋都能被覆盖
                return true;
        }
        return false;         // 还有些房屋不能被覆盖
    }
}

思路二：二分查找

看了别人的题解，大多数的思路是遍历 houses，然后用二分法找到离这个 house 最近的供暖期，每次都维护 res，使其能满足全部供暖的最小值。时间复杂度也是 O(nlogn)。

class Solution {
    public int findRadius(int[] houses, int[] heaters) {
        int res = 0;                  		// 结果
        int n = heaters.length;       		// 供暖器的数量
        Arrays.sort(heaters);         		// 供暖期排序
        for (int house : houses){        	// 遍历每个房间
            int left = 0, right = n;
            while (left < right){       	// 找到这个房间距离最小的供暖器
                int mid = left + (right - left) / 2;
                if (house > heaters[mid])
                    left = mid + 1;
                else
                    right = mid;
            }
            // 得到的 right 对应在房子的右边
            // 如果 right 为0，则说明房子左边每供暖器，right 为 n，则说明房子右边没供暖器
            int dist1 = (right == 0) ? Integer.MAX_VALUE : Math.abs(house - heaters[right - 1]);
            int dist2 = (right == n) ? Integer.MAX_VALUE : Math.abs(house - heaters[right]);
            res = Math.max(res, Math.min(dist1, dist2));
        }
        return res;
    }
}

③ 378. 有序矩阵中第 K 小的元素

https://leetcode-cn.com/problems/kth-smallest-element-in-a-sorted-matrix/

这道题一开始没什么思路。如果是一维数组的话则可以参考快排的思路。看了下题解，也是用到了

二分法猜结果

。

范围：[martix[0][0] ~ matrix[n-1][n-1]]，最值：最接近第 k 小（最接近nums[k]的值）：例如数组中的第 k，k+1 小的值分别为 5， 8，则在范围内第 k 小的值可以是 5， 6，7，则我们继续求最接近 5 的，故可以继续缩小范围。

思路：

• 从范围中找到中位数，判断其中位数排在数组的第几位
  • 若排的位数大于等于 k，则减小值
  • 若排的位数小于 k，则增大值
• 判断中位数排第几位的思路：
  
  
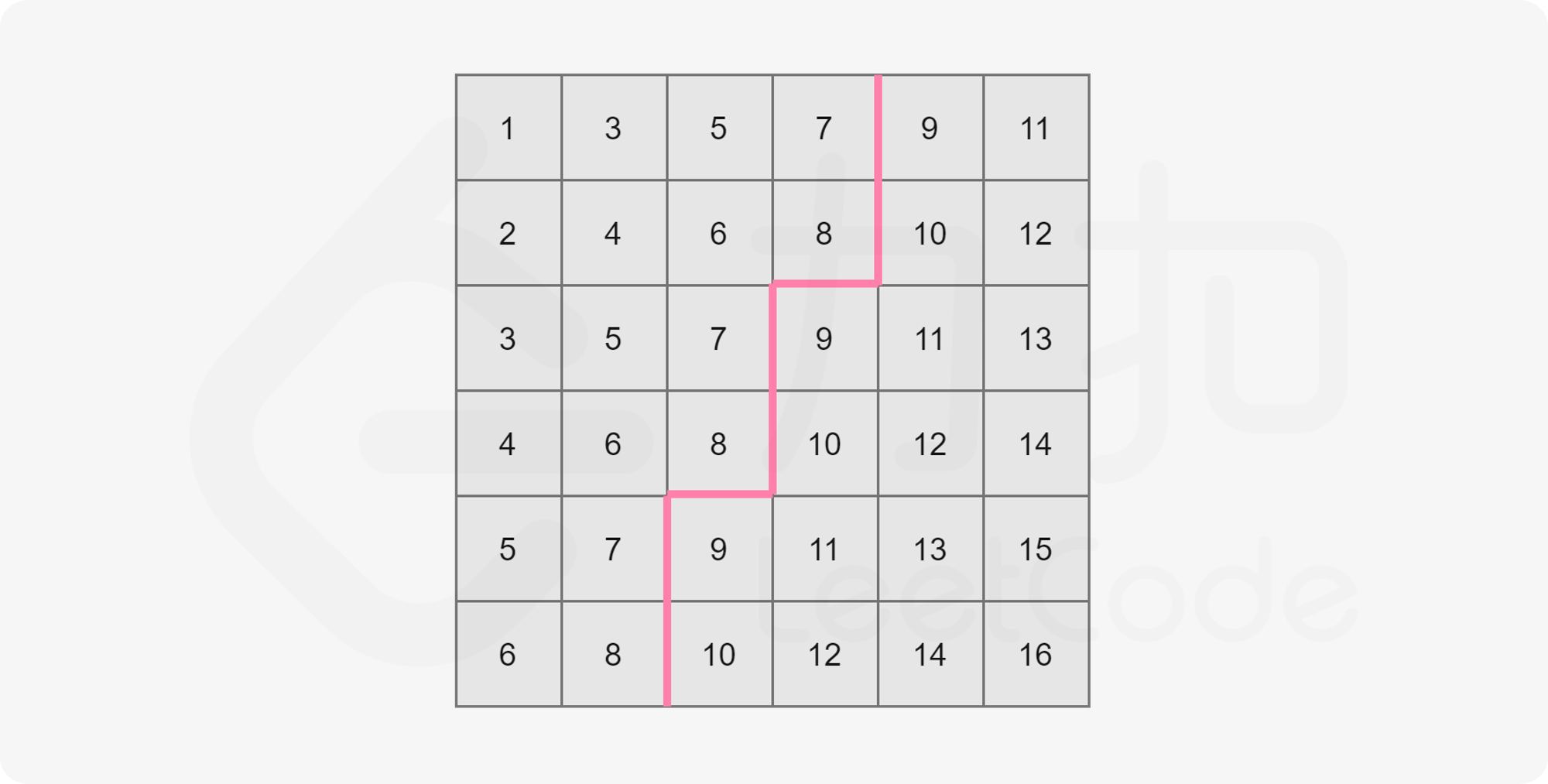
  • 可以看出从左下到右上是呈阶梯状的，即当 matrix[i][j] > mid，则 matrix[i][j+1] 必然 > k

class Solution {
    int[][] matrix;

    public int kthSmallest(int[][] matrix, int k) {
        this.matrix = matrix;         // 设为全局变量
        int n = matrix.length;
        int left = matrix[0][0], right = matrix[n-1][n-1];    // 找出范围

        while (left < right){
            int mid = left + (right - left) / 2;    
            if (checkNum(mid, k))      // 判断这个值是否大于第 k 小
                right = mid;
            else
                left = mid+1;
        }
        return right;
    }

    public boolean checkNum(int mid, int k){
        int n = matrix.length;
        int i = n - 1, j = 0;
        int res = 0;
        while (i >= 0 && j < n){
            if (matrix[i][j] <= mid){       // 当前列（到i）小于 mid，则直接加，在判断下一列
                res += i+1;
                j++;
            }else{
                i--;      // 当前列（到i）大于 mid，则减少一个单元，再判断
            }
        }
        return res >= k;     // 个数是否大于 k
    }
}

总结

这周的题目很有质量，集中一个点重拳出击。而且还是

二分法猜结果

这种进阶题。爆赞👍！！