点集Q的凸包(ConvexHull)就是一个最小的凸多边形,满足Q中的每个点都在P的边界上或者在P的内部。我们常常用CH(Q)来表示点集Q的凸包。
(CH即convex hull的缩写)
得到的输出一般来讲都是按照逆时针顺序输出的凸包的各个顶点
。
首先从算法角度审视一下这个问题吧,这个问题的时间复杂度得下界到底是多少呢
我们使用规约法,首先将排序问题归约到求凸包的问题,即通过映射将序列x
1
,x
2
,x
3
…x
n
,变成凸包中的点(x
1
,x
1
2
),(x
2
,x
2
2
)…(x
n
,x
n
2
)

从序列规约到点集,只需要对每一个数据做平方操作,总体时间复杂度为O(n)。而由于凸包求解出的数据是按照顺/逆时针输出的,所以,从凸包求解好的问题得到排序复杂度也是O(n)

我们已经知道了排序算法的时间复杂度的下界是Θ(nlogn),所以可以得到凸包算法的复杂度下界一定是高于排序的,也就也是Θ(nlogn)
这里面介绍两种算法

1、Graham扫描法
基本思想:通过设置一个关于候选点的堆栈s来解决凸包问题。
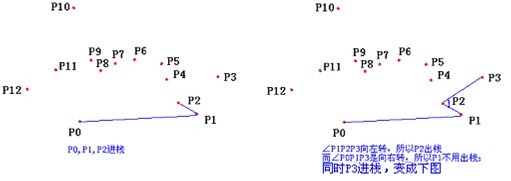
操作:输入集合Q中的每一个点都被压入栈一次,非CH(Q)(表示Q的凸包)中的顶点的点最终将被弹出堆栈,当算法终止时,堆栈S中仅包含CH(Q)中的顶点,其顺序为个各顶点在边界上出现的逆时针方向排列的顺序。
注:下列过程要求|Q|>=3,它调用函数TOP(S)返回处于堆栈S 顶部的点,并调用函数NEXT-TO –TOP(S)返回处于堆栈顶部下面的那个点。但不改变堆栈的结构。
GRAHAM-SCAN(Q)
1 设P
0
是Q 中Y 坐标最小的点,如果有多个这样的点则取最左边的点作为P
0
;
2 设< P
1
,P
2
,……,P
m
>是Q 中剩余的点,对其按逆时针方向相对P0 的极角进行排序,如果有数个点有相同的极角,则去掉其余的点,只留下一个与P0 距离最远的那个点;
3 PUSH(p
0
, S)
4 PUSH(p
1
, S)
5 PUSH(p
3
, S)
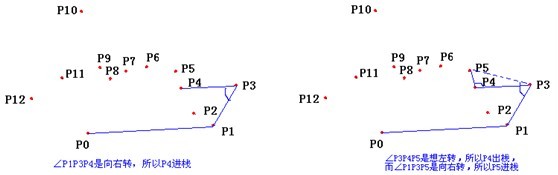
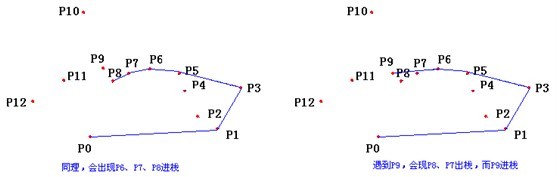
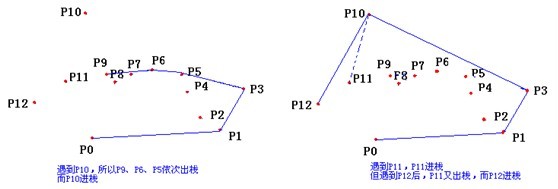
6 for i ← 3 to m
7 do while 由点NEXT-TOP-TOP(S),TOP(S)和Pi 所形成的角形成一次非左转
8 do POP(S)
9 PUSH(p
i
, S)
10 return S
图解如下


2、Jarvis March算法,又称gift wrapping算法
概述:也可称为卷包裹法,思路是先找到一个在凸包上的点,然后卷过去,由于每次确定凸包上的一个点需要遍历所有的点,因此时间复杂度为O(N*H),其中N为全部点的数目,H为凸包上的点数目;
方法和步骤:(下述采用固定两点的方式)
(1)找到位于最低最左边的点p0,最高最右边的点pk,则此两点必为凸包上的点;
(2)对逆时针方向排列的顶点序列按p0pk构造右链,左链;
(3)右链构造:设定一个栈,先将p0入栈,对其他的点依据相对于栈顶元素的最小极角,并距离最远的点入栈,左链同理;
(4)核心:如何求相对于栈顶元素的最小极角?
设pk为最高点,p0位栈顶元素;
只要栈顶元素不是pk,循环做以下工作:
pm=pk;
for(int i=0;i<n;i++)//依次考查其他的点p[i],是否有相对于p[top]的最小极角
if((p[top]p[i]×p[top]pm>0)
pm=p[i];
经过上述一次遍历,得到的pm为相对于当前p[top]的具有最小极角的顶点,即右链中连接p[top]的下一个凸包的顶点;
左链同理,即可实现