经常在目标检测,分割的paper中看到mAP这样的评价标准,
那么mAP到底是什么呢?
AP(Average precision)是评价目标检测和分割的标准,有box mAP, mask mAP.
看名称Average precision, 就能猜到是计算precision的均值。
它其实计算的是大家熟知的precision, recall图中,不同recall对应的precision的均值(ROC curve下面积)。
所以要从precision, recall, IOU入手。
IOU
如果是目标框,计算的就是目标框的intersection / union

如果是mask, intersection计算的是点积(mask拉成一维,再点积)
上代码比较容易明白。
def mask_iou(masks_a, masks_b, iscrowd=False):
"""
Computes the pariwise mask IoU between two sets of masks of size [a, h, w] and [b, h, w].
The output is of size [a, b].
"""
masks_a = masks_a.view(masks_a.size(0), -1)
masks_b = masks_b.view(masks_b.size(0), -1)
intersection = masks_a @ masks_b.t()
area_a = masks_a.sum(dim=1).unsqueeze(1)
area_b = masks_b.sum(dim=1).unsqueeze(0)
return intersection / (area_a + area_b - intersection) if not iscrowd else intersection / area_a
precision, recall
直接上公式了

简单地说,
precision就是在目前为止你预测的样本里面,预测正确的比例
。
而
recall就是目前为止你预测正确的个数,占总的正样本个数的比例
。
一个是目前预测的范围里面的正确率,一个是总的正确率。
如果想提高recall, 就拼命多预测,总能把正确的都揪出来,但是预测越多错的越多,precision就会降低。
如果想提高precision, 那么就保守点,预测对了就不预测了,但是这样就没法把所有的都预测出来,recall会降低。
而怎么判断你预测的是positive还是negative呢,这时候就需要IOU登场了,
计算IOU,然后根据不同的阈值(COCO AP标准中,阈值从0.5~0.95),
IOU > 阈值,那就是positive, 否则是negative.
前面说过了,precision是你预测的一堆positive里面,真正的positive的比例。
那你预测的时候肯定是一个一个预测的,不是一下子预测一堆的,
所以precision需要一个一个来。
而recall,正样本的个数是已知的,所以需要根据一个一个预测出的正确的positive除以这个正样本个数。
举个例子:
假设IOU阈值是0.5, 根据这个阈值来判断positive和negative.
假设正样本一共有5个苹果,把图像中所有的对苹果的预测按score降序排列。
下面来看看precision和recall怎么计算的。
预测是一个一个预测的,所以要一行一行看,
第1行,预测对了一个positive, 总共也就预测了这一个,所以precision = 1/1 = 1.0,
而正样本一共有5个,所以recall = 1/5 = 0.2
跳到第3行,现在已经预测了3个,其中预测正确的占俩,所以precision=2/3=0.67,
而正样本一共有5个,目前为止预测正确的有俩,所以recall = 2/5 = 0.4.
后面依次类推。

下面要说到AP了
AP
AP(Average Precision)定义为precision-recall曲线下的面积。
先看看precision-recall曲线吧,
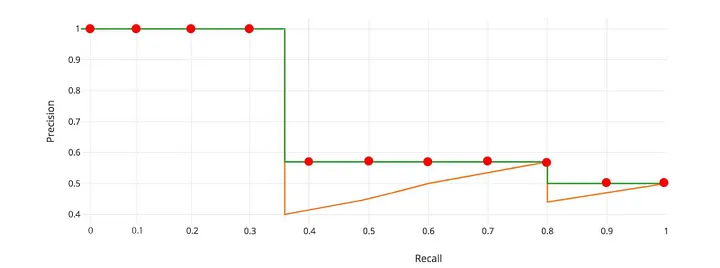
把上面的每对(precision, recall) 画成一个点,然后把这些点连线,就得到下图。
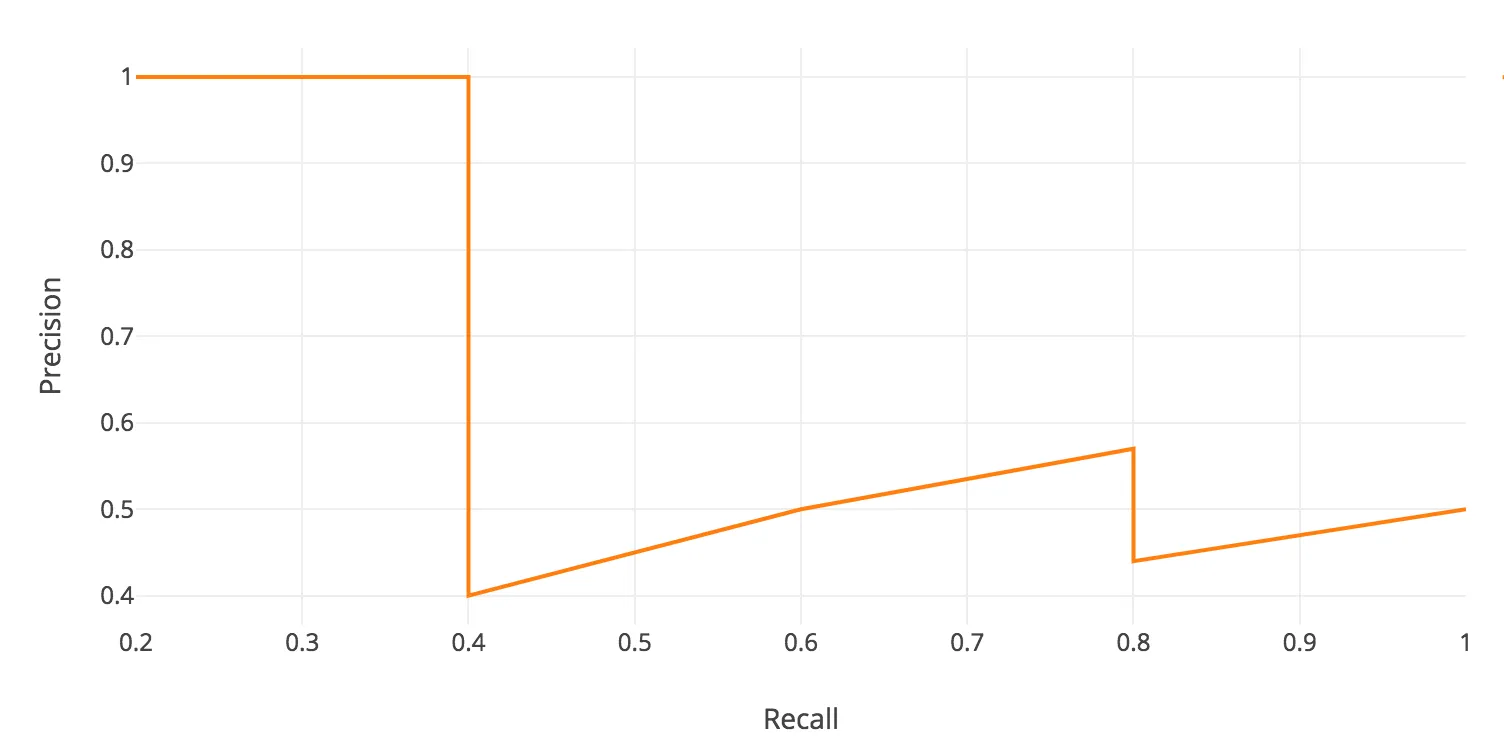
precision-recall都是0~1的,所以
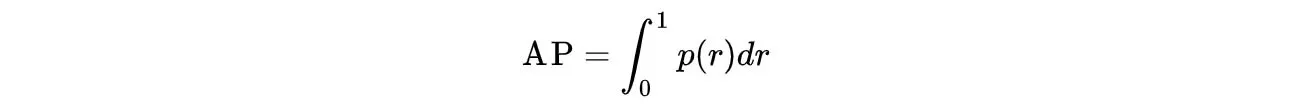
这个曲线不够平滑,需要先做平滑,
一般,是从右到左,当左边一格比右边一格的值小时,换成右边一格的值。
i : n ~ 0, precision[i] = max(precision[i], precision[i+1]),
所以平滑成如下绿色的曲线。
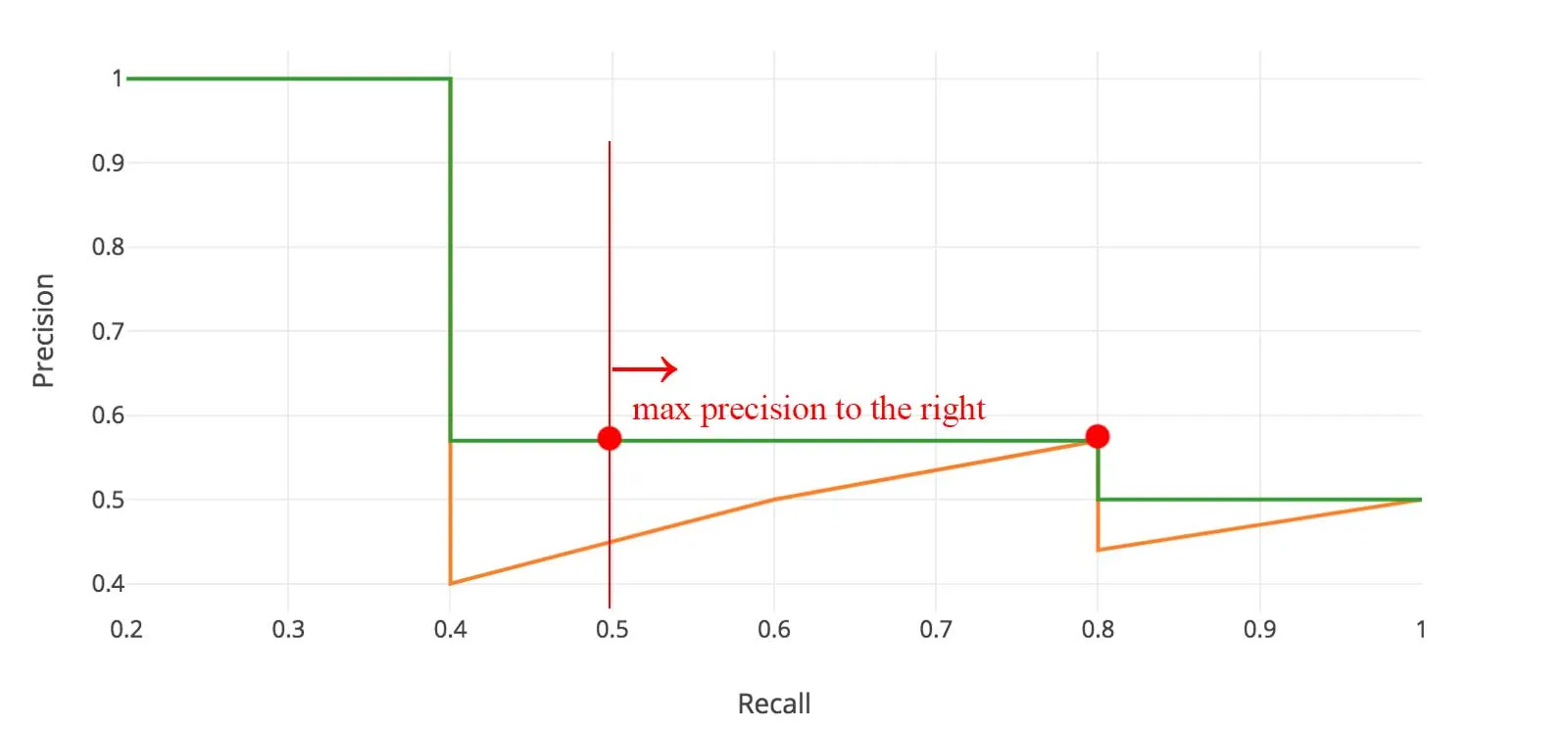
插值法AP
在Pascal VPC2008中,用的是11点插值法计算AP,
也就是在recall值的0~1.0中取11个点:0, 0.1, 0.2, …, 0.9, 1.0
然后把每个recall值对应的precision值加起来,再求平均
可以看到有precision中有5个1,4个0.57, 2个0.5,
所以AP = (5 × 1.0 + 4 × 0.57 + 2 × 0.5)/11
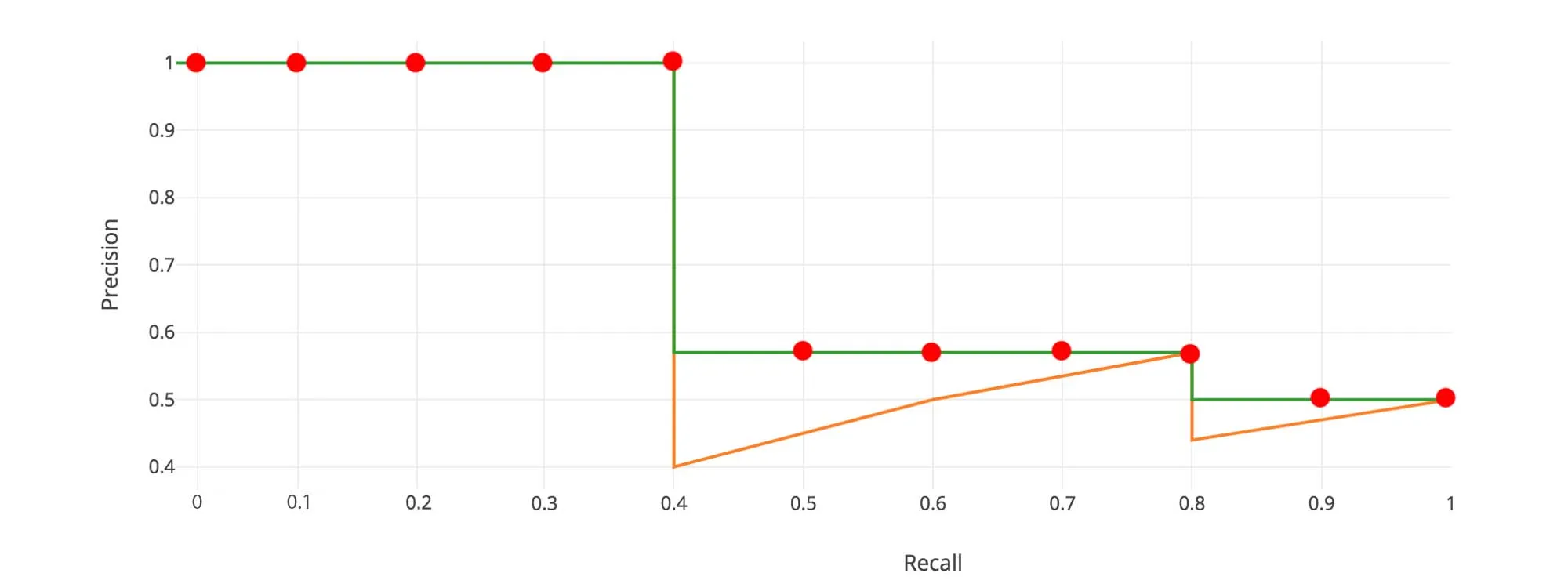
如果AP变得很小了,那么剩余项就不需要再加上求平均了,假设剩余项都是0,因为加上的还不够平均的。不需要非要加到recall=1.0的地方。
也就是说precision降到可忽略的程度,就可以不用再加了。
PASCAL VOC中有20个不同的classes, 那么就对每一个class计算AP,最后计算20个AP的平均值。
为什么是11点插值呢?
The intention in interpolating the precision/recall curve in this way is to
reduce the impact of the “wiggles” in the precision/recall curve, caused by
small variations in the ranking of examples.
插值法AP有2个缺点:
1.不够precise
2.如果是low AP的情况,这种方法就不能很好地区分不同的methods.
所以,在PASCAL VOC 2008之后又有了不同的AP计算方法。
AP(AUC曲线下的面积)
在VOC2010 ~ 2012中,每当precision值下降,都会采样对应的unique recall值,
根据precision值,和r2 – r1, 就能计算对应区域的面积,
这些面积加起来,就是AUC曲线下的面积。
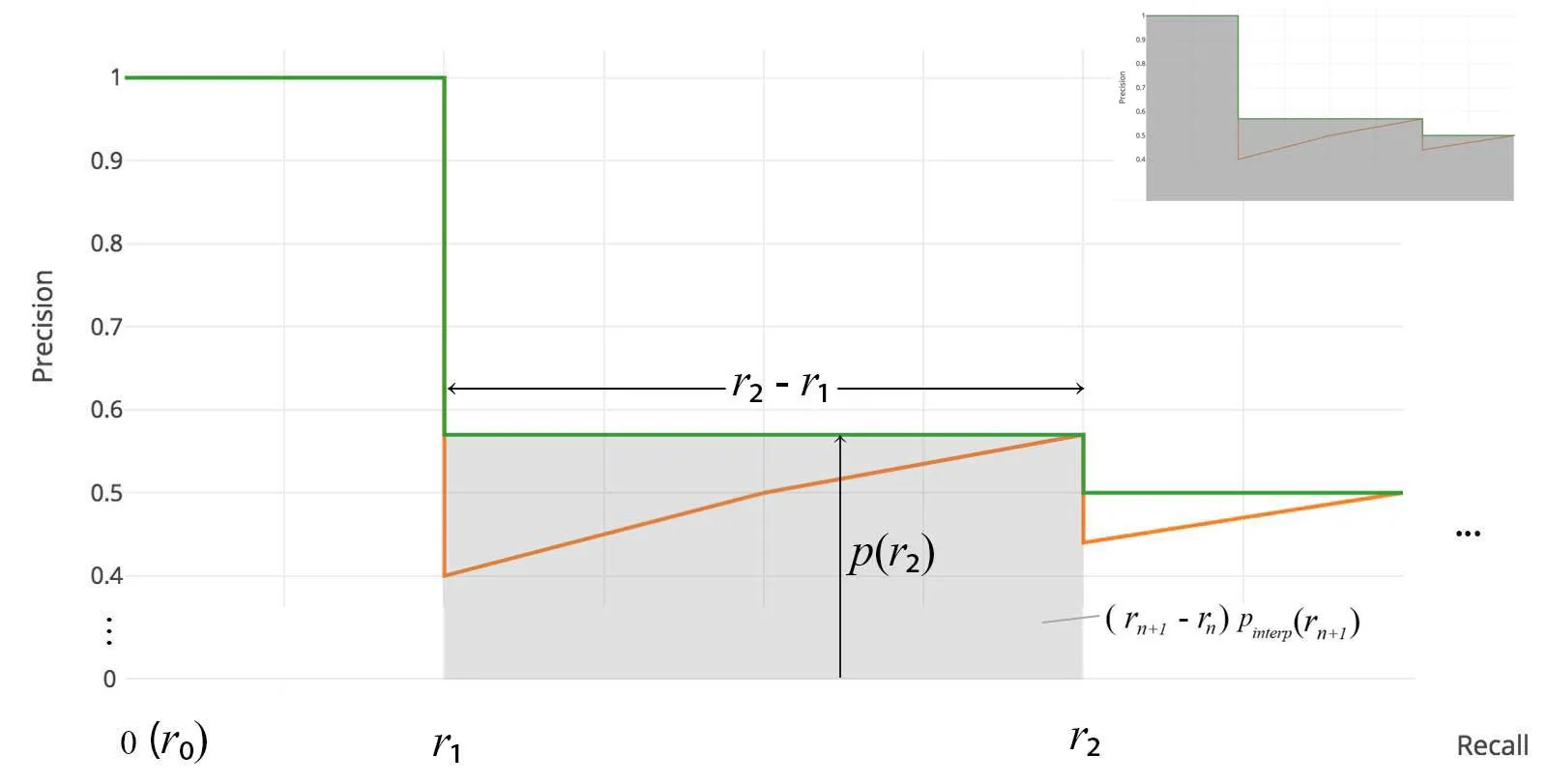
所以不需要插值,也不是固定地采样11个点,而是每当precision下降,就采样对应的recall值,
计算对应矩形的面积。
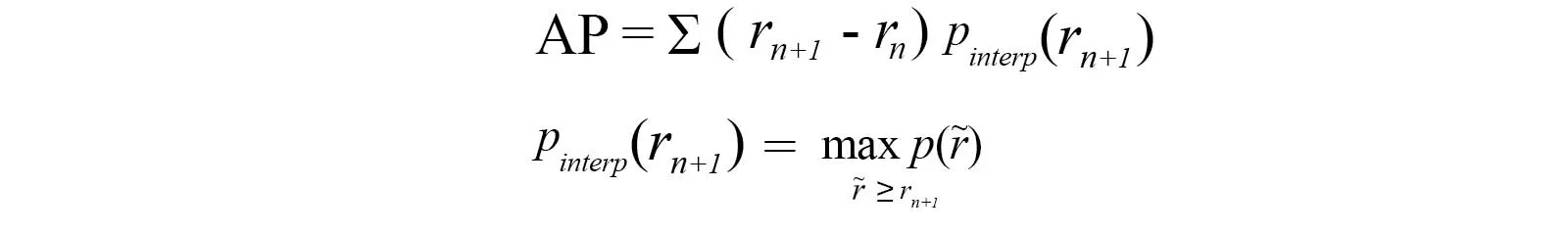
看下面的例子,11点插值法没有捕捉到第一个precision下降的地方,所以两种方法会有不同。
插值法AP = (4 * 1 + 5 * 0.57 + 2 * 0.5) / 11 = 0.7136
AUC法AP = 1*(0.36-0)+0.57*(0.8-0.36)+0.5*(1-0.8) = 0.7108
COCO mAP
对于COCO数据集,COCO mAP用的是101个点的插值来计算的。
且AP是对多个IOU的平均,例如AP[0.5:0.95]就是把IOU阈值在[0.5, 0.95]之间每隔0.05取值(一共10个阈值),
算出来10个阈值下的AP,那么COCO数据集有80个class,
所以计算的是10个IOU阈值下,每个class的AP,最后的mAP,就是这10×80个AP的平均值。
看下COCO数据集的其他metrics。
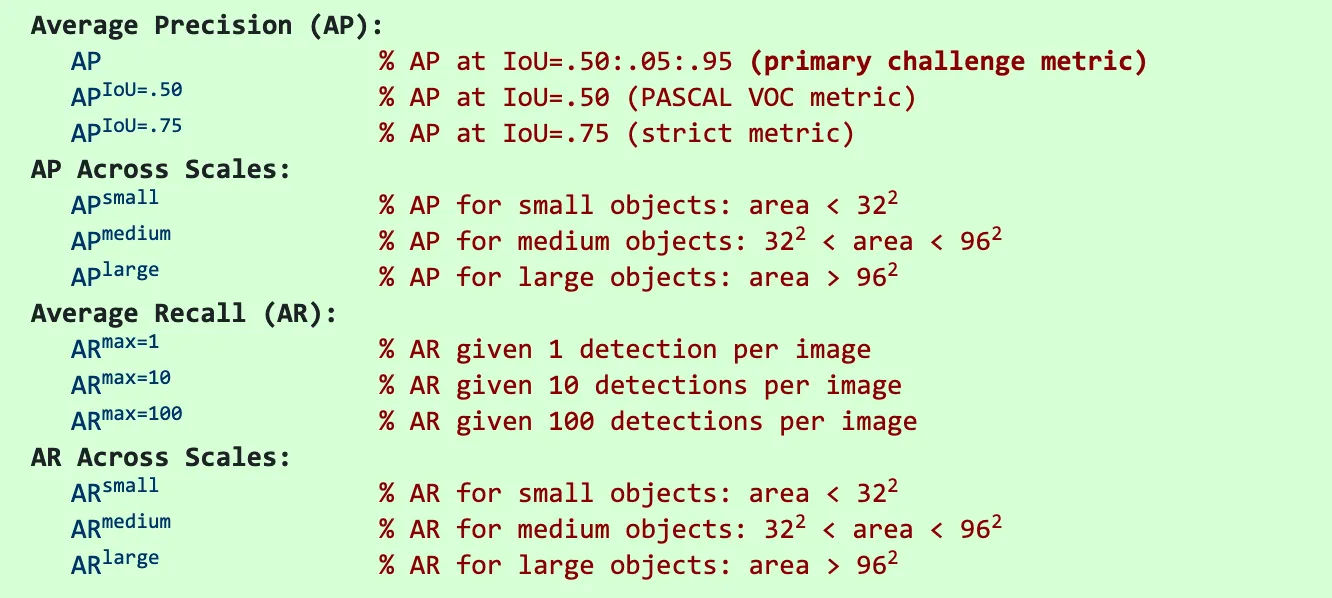
下面两个图分别是yolov3的AP和yolact的AP。
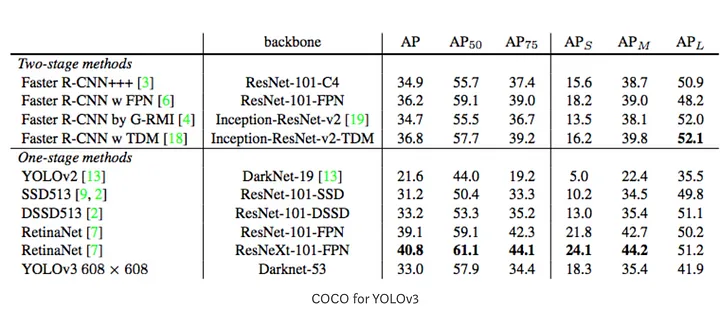

最后说下,mAP(mean average precision) 就是AP的均值,计算每个class的AP然后取平均值。
有时候,mAP和AP是一个东西。例如在COCO中,它们就是一样的。
AP is averaged over all categories. Traditionally, this is called “mean average precision” (mAP).
We make no distinction between AP and mAP (and likewise AR and mAR) and assume
the difference is clear from context.