题目链接:
PTA | 程序设计类实验辅助教学平台
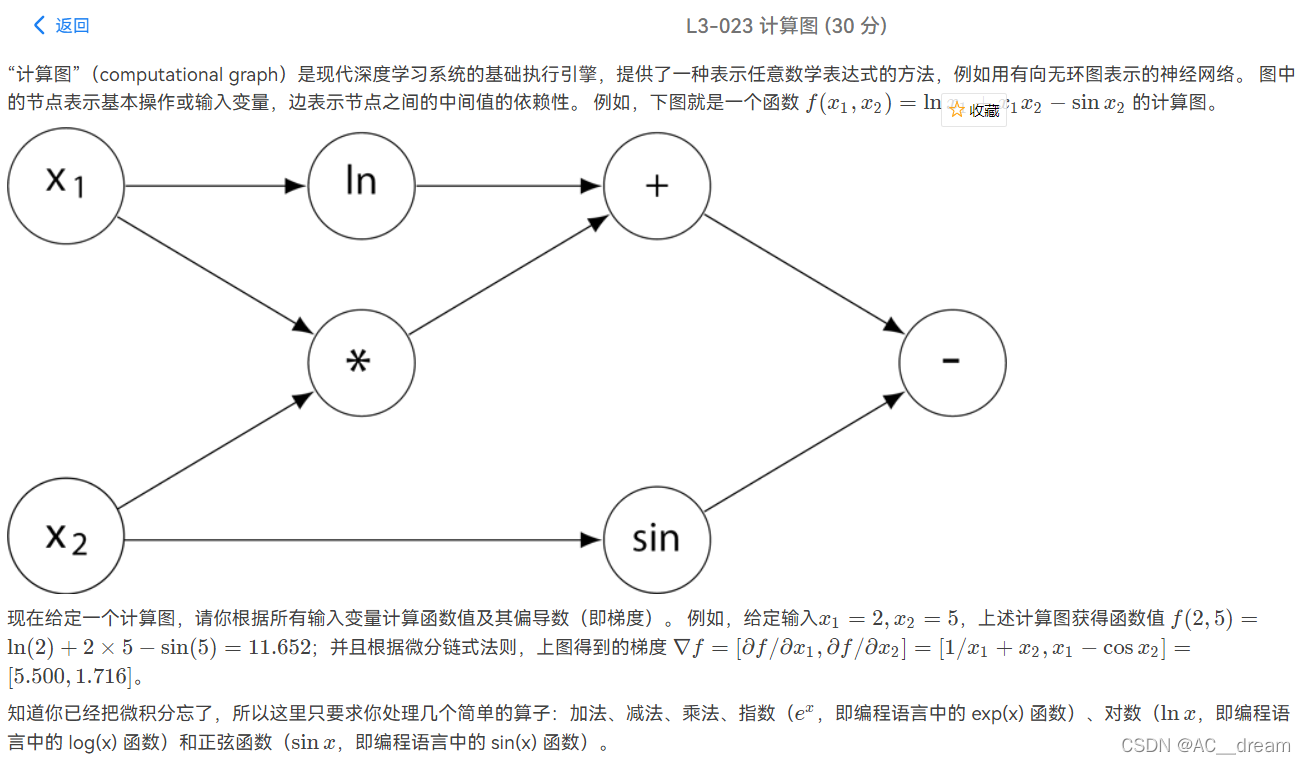

输入样例:
7
0 2.0
0 5.0
5 0
3 0 1
6 1
1 2 3
2 5 4
输出样例:
11.652
5.500 1.716分析:这道题就是一个基本的搜索:
先来说一下怎么计算图的函数值:
假如
有x号节点u和y号节点v要进行z号运算,我们就从z号节点向x号节点和y号节点各连一条边
,由于图一定是个拓扑图,
假如我们递归到z号节点,就必须要把x号节点和y号节点的值全算出来
,所以这显然是一个递归搜索的过程,
终止条件就是我们遍历到类型为0的点,也就是叶子节点,直接返回叶子节点的值
即可。
下面来说一下如何计算梯度的值:
这个就是模拟复合函数求导的方法,类似于上面计算图的函数值的方法,但是又要加上求导这个过程,举个例子来说,5号节点是乘法运算,其中连着3号和4号节点,那么我们对5号节点求导运算按照乘法的求导法则就相当于对4号节点求导并乘以3号节点的函数值再加上对3号节点求导并乘以4号节点的函数值,其他求导过程也是分别按照各自的求导法则来进行。
求导运算的终止条件就不是单纯地遍历到叶子节点了,还需要判断叶子节点的编号是不是我们要求导的变量,如果是就返回1(x的导数为1),不是就返回0
.
最后说一个坑,就是这道题目对精度要求比较严格,我一开始把e按照2.71828来算,也就是用pow函数来求e^x,但总无法过第3个测试点,后来
直接用exp函数就过了
,希望大家也注意一下这一点。
下面是代码:
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
const int N=1e6+10;
int h[N],ne[N],type[N],e[N],idx;
int chu[N],st[N];
double w[N];
void add(int x,int y)
{
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
double cal(int x)
{
if(fabs(w[x]+999999999)>0.1) return w[x];//记忆化搜索
if(type[x]==0) return w[x];
else if(type[x]==1)
w[x]=cal(e[ne[h[x]]])+cal(e[h[x]]);
else if(type[x]==2)
w[x]=cal(e[ne[h[x]]])-cal(e[h[x]]);
else if(type[x]==3)
w[x]=cal(e[ne[h[x]]])*cal(e[h[x]]);
else if(type[x]==4)
w[x]=exp(cal(e[h[x]]));
else if(type[x]==5)
w[x]=log(cal(e[h[x]]));
else
w[x]=sin(cal(e[h[x]]));
return w[x];
}
double der(int x,int t)//对t求导
{
if(x==t) return 1;//对x求导为1
if(type[x]==0) return 0;//对常数求导为0
else if(type[x]==1)
return der(e[ne[h[x]]],t)+der(e[h[x]],t);
else if(type[x]==2)
return der(e[ne[h[x]]],t)-der(e[h[x]],t);
else if(type[x]==3)
return der(e[ne[h[x]]],t)*cal(e[h[x]])+der(e[h[x]],t)*cal(e[ne[h[x]]]);
else if(type[x]==4)
return exp(cal(e[h[x]]))*der(e[h[x]],t);//注意这个地方不能将e按2.71828算,精度损失比较严重
else if(type[x]==5)
{
if(cal(e[h[x]]))
return der(e[h[x]],t)/cal(e[h[x]]);
return 0;
}
else
return cos(cal(e[h[x]]))*der(e[h[x]],t);
}
int main()
{
memset(h,-1,sizeof h);
int n;
cin>>n;
for(int i=1;i<=n;i++) w[i]=-999999999;
int tt=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&type[i]);
if(type[i]==0)
{
scanf("%lf",&w[i]);//记录对哪些数进行求导
st[++tt]=i;
}
else if(type[i]==1||type[i]==2||type[i]==3)
{
int u,v;
scanf("%d%d",&u,&v);
u++;v++;//使编号从1开始
add(i,u);add(i,v);
chu[u]++;chu[v]++;
}
else if(type[i]==4||type[i]==5||type[i]==6)
{
int u;
scanf("%d",&u);
u++;add(i,u);chu[u]++;
}
}
int root;
for(root=1;root<=n;root++)
if(!chu[root]) break;
printf("%.3lf\n",cal(root));
printf("%.3lf",der(root,st[1]));
for(int i=2;i<=tt;i++)
printf(" %.3lf",der(root,st[i]));
return 0;
}