1、概念
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
2、基本思想
在包含问题的所有解的解空间树中,按照
深度优先搜索的策略
,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。
若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。
而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
3、用回溯法解题的一般步骤:
(1)针对所给问题,确定问题的解空间:
首先应明确定义问题的解空间,问题的解空间应至少包含问题的一个(最优)解。
(2)确定结点的扩展搜索规则
(3)以
深度优先方式搜索
解空间,并在搜索过程中用剪枝函数避免无效搜索。
4、算法框架
(1)问题框架
设问题的解是一个n维向量(a1,a2,………,an),约束条件是ai(i=1,2,3,…..,n)之间满足某种条件,记为f(ai)。
(2)非递归回溯框架
int a[n],i;
初始化数组a[];
i = 1;
while (i>0(有路可走) and (未达到目标)) // 还未回溯到头
{
if(i > n) // 搜索到叶结点
{
搜索到一个解,输出;
}
else // 处理第i个元素
{
a[i]第一个可能的值;
while(a[i]在不满足约束条件且在搜索空间内)
{
a[i]下一个可能的值;
}
if(a[i]在搜索空间内)
{
标识占用的资源;
i = i+1; // 扩展下一个结点
}
else
{
清理所占的状态空间; // 回溯
i = i –1;
}
}
}(3)递归的算法框架
回溯法是对解空间的深度优先搜索,在一般情况下使用递归函数来实现回溯法比较简单,其中i为搜索的深度,框架如下:
int a[n];
try(int i)
{
if(i>n)
输出结果;
else
{
for(j = 下界; j <= 上界; j=j+1) // 枚举i所有可能的路径
{
if(fun(j)) // 满足限界函数和约束条件
{
a[i] = j;
... // 其他操作
try(i+1);
回溯前的清理工作(如a[i]置空值等);
}
}
}
}
五 八皇后问题
(1)问题介绍
八皇后问题是一个以国际象棋为背景的问题:如何能够在 8×8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。

转化规则:其实八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅
当 n = 1 或 n ≥ 4
时问题有解。令一个一维数组a[n]保存所得解,其中a[i] 表示把第i个皇后放在第i行的列数(注意i的值都是从0开始计算的),下面就八皇后问题的约束条件。
(1)因为所有的皇后都不能放在同一列,因此任意两个a[0]…..a[7]的值不能存在相同的两个值。
(2)所有的皇后都不能在对角线上,那么该如何检测两个皇后是否在同一个对角线上?我们将棋盘的方格成一个二维数组,如下:

假设有两个皇后被放置在(i,j)和(k,l)的位置上,明显,当且仅当|i-k|=|j-l| 时,两个皇后才在同一条对角线上。
法一 穷举法
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
int n; //n皇后问题,当n为8时,就是八皇后问题
int a[9];
bool chongtu(int a[])
{
for(int i=1;i<8;i++)
{
for(int j=i+1;j<=8;j++)
{
if(a[i]==a[j]||abs(a[i]-a[j])==(j-i))
return true;
}
}
return false;
}
int main()
{
int count_=0;
memset(a,0,sizeof(a));
for(a[1]=1;a[1]<=8;a[1]++)
for(a[2]=1;a[2]<=8;a[2]++)
for(a[3]=1;a[3]<=8;a[3]++)
for(a[4]=1;a[4]<=8;a[4]++)
for(a[5]=1;a[5]<=8;a[5]++)
for(a[6]=1;a[6]<=8;a[6]++)
for(a[7]=1;a[7]<=8;a[7]++)
for(a[8]=1;a[8]<=8;a[8]++)
{
if(chongtu(a))
continue;
else
{
++count_;
cout<<"第"<<count_<<"个八皇后排列为:";
for(int i=1;i<=8;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
}
}
return 0;
}

但是时间复杂度太高了。。。。当过程中某一个节点已经不满足时,继续往下走。这种方法会穷举所有的情况。。。
法二 回溯法的递归解法
#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
using namespace std;
const int maxn=100; //最多为100皇后
int a[105];
int n; //n皇后,当n为8时,就是八皇后问题
int cnt;
bool chongtu(int a[],int n)
{
for(int i=1;i<n;i++)
{
for(int j=i+1;j<=n;j++)
{
if(a[i]==a[j]||abs(a[i]-a[j])==(j-i))
return true;
}
}
return false;
}
void Question(int a[],int k) //开始安置第k个皇后
{
if(k>n) //说明已经放置完毕
{
cnt++;
cout<<"第"<<cnt<<"个皇后排列为:";
for(int i=1;i<=n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
}
else
{
for(int i=1;i<=n;i++) //枚举所有可能
{
a[k]=i;
if(!chongtu(a,k)) //提前判断是否与前面冲突,如果不冲突,放置第k+1个皇后
Question(a,k+1);
}
}
return ;
}
int main()
{
cin>>n;
memset(a,0,sizeof(a));
cnt=0;
Question(a,1); //从第一个皇后开始放置
return 0;
}可以看出,当放置第k个皇后时,枚举所有可能出现的位置,然后马上判断是否冲突,如果不冲突,再安置第k+1个皇后,如果冲突,就回溯。。

可以看出没有3皇后。。

答案一样。。。
法三 回溯法的非递归解法
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
const int maxn=105;
int a[maxn];
int n;
int cnt;
bool chongtu(int a[],int n)
{
for(int i=1;i<n;i++)
{
for(int j=i+1;j<=n;j++)
{
if(a[i]==a[j]||abs(a[i]-a[j])==(j-i))
return true;
}
}
return false;
}
void Question()
{
int k=1;
while(k>0) //k==0时,表示找完了所有的情况
{
a[k]+=1; //第k行第一列放一个皇后
while(a[k]<=n&&chongtu(a,k)) //若没有超出列范围且摆放冲突
a[k]+=1; //摆放到下一列
if(a[k]<=n)
{
if(k==n) //全部摆放完成
{
cout<<"第"<<++cnt<<"个皇后排列为:";
for(int i=1;i<=n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
}
else //未摆放完成
k+=1;
}
else //说明目前所有位置都冲突了,需要回溯
{
a[k]=0; //清除之前的
k-=1;
}
}
return ;
}
int main()
{
cin>>n;
cnt=0;
memset(a,0,sizeof(a));
Question();
return 0;
}

法四 排列组合的方法
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
int n;
int cnt;
void swap_int(int *a,int*b)
{
int temp=*a;
*a=*b;
*b=temp;
}
bool chongtu(int a[],int n)
{
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++)
{
if(abs(a[i]-a[j])==(j-i))
return true;
}
}
return false;
}
void permutation(int a[],int b[])
{
if(b>a+(n-1)) //一个排列已经出来
{
if(!chongtu(a,n))
{
cout<<"第"<<++cnt<<"个皇后排列为: ";
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
cout<<endl;
return ;
}
}
for(int *s=b;s<=a+(n-1);s++)
{
swap_int(s,b);
permutation(a,b+1);
swap_int(s,b);
}
return;
}
int main()
{
cin>>n;
int a[n];
cnt=0;
for(int i=0;i<n;i++)
{
a[i]=i;
}
permutation(a,a);
return 0;
}
六 N个数选取K个数使其和等于M,输出所有方案
(1)如果每个数可以被选择无数次
典型的回溯法应用。
对数组里面的每个数,用递归的方式相加,每次递归将和sum与target作比较,若相等则加入结果vector,sum>target则舍弃,并返回false,若sum<target,则继续进行递归。若sum>target,则回溯到上一层,重新以数组中的下一个数开始递归。
第一种sum=target的情况下,在加入结果vector后回溯(此时不应再累加),要将当前一种结果最后加入的元素pop_back(),并继续对后面的元素进行递归;
第二种sum>target的情况下,则需要将当前结果的最后加入的元素pop_back(),并继续对后面的元素进行递归。
第三种sum<target的情况下,直接以当前数继续递归。
注意元素可以重复,所以下一次递归总是从当前递归元素开始。
#include <cstdio>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int m;
int k;
vector<vector<int> > res; //最终的组合
//从ori中(从index开始)选取一个数据到subres中,目标是subres中所有元素和为target,处理第index元素之前和是sum
void dfs(vector<int> &ori,vector<int> &subres,int index,int sum,int target)
{
if(sum==target) //已经满足条件,回溯
{
res.push_back(subres);
return;
}
for(int i=index;i<ori.size();i++)
{
if(ori[i]>target||(sum+ori[i])>target) //这个路径不对,回溯
return;
subres.push_back(ori[i]);
dfs(ori,subres,i,sum+ori[i],target); //执行一个深度上的组合,并计算和
subres.pop_back(); //没执行完一个深度的组合就弹掉末尾元素
}
}
int main()
{
cin>>m>>k; //从m个元素中选择元素,使其和为k,每个元素可以使用多次
vector<int> ori;
for(int i=0;i<m;i++)
{
int temp;
cin>>temp;
ori.push_back(temp);
}
//先排序
sort(ori.begin(),ori.end());
vector<int> subres; //每一个组合
dfs(ori,subres,0,0,k); //第一个0代表起始元素的下标,第二个0代表当前和为0
//输出所有组合
for(int i=0;i<res.size();i++)
{
for(int j=0;j<res[i].size();j++)
{
if(j!=res[i].size()-1)
cout<<res[i][j]<<" ";
else
cout<<res[i][j]<<endl;
}
}
return 0;
}
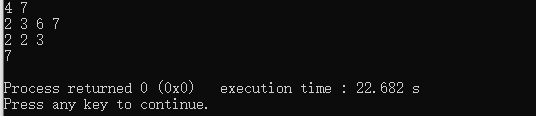
其实代码可以再优化,因为已经排好序了,所以当出现ori[i]>target||(sum+ori[i])>target可以直接break,因为之后的肯定也都满足啊。下面的例子同理
(2)如果每个元素只可以被选择一次
把上述代码稍微改下就可以了,每次选择元素都是从下一个开始即可,不能重复选择。注意有个去重问题。。。
#include <cstdio>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int m;
int k;
vector<vector<int> > res; //最终的组合
//从ori中(从index开始)选取一个数据到subres中,目标是subres中所有元素和为target,处理第index元素之前和是sum
void dfs(vector<int> &ori,vector<int> &subres,int index,int sum,int target)
{
if(sum==target) //已经满足条件,回溯
{
res.push_back(subres);
return;
}
for(int i=index;i<ori.size();i++)
{
if(ori[i]>target||(sum+ori[i])>target) //这个路径不对,回溯
return;
//重复的情况
if(i&&(ori[i]==ori[i-1])&&i>index)
continue;
subres.push_back(ori[i]);
dfs(ori,subres,i+1,sum+ori[i],target); //执行一个深度上的组合,并计算和
subres.pop_back(); //没执行完一个深度的组合就弹掉末尾元素
}
}
int main()
{
cin>>m>>k; //从m个元素中选择元素,使其和为k,每个元素只可以使用一次
vector<int> ori;
for(int i=0;i<m;i++)
{
int temp;
cin>>temp;
ori.push_back(temp);
}
//先排序
sort(ori.begin(),ori.end());
vector<int> subres; //每一个组合
dfs(ori,subres,0,0,k); //第一个0代表起始元素的下标,第二个0代表当前和为0
//输出所有组合
for(int i=0;i<res.size();i++)
{
for(int j=0;j<res[i].size();j++)
{
if(j!=res[i].size()-1)
cout<<res[i][j]<<" ";
else
cout<<res[i][j]<<endl;
}
}
return 0;
}
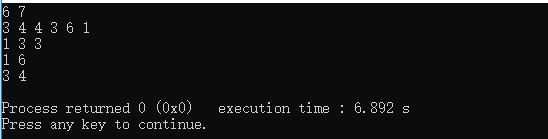
其实也可以直接用dfs解决,更简单理解,但可能时间复杂度更高。。。
案例
题目一


#include <cstdio>
#include <iostream>
using namespace std;
int n;
//当处理第i个元素之前,武力值和金币值分别已经为sumd,sump,最小金币值一直在变化,所以用引用。
//其他不加引用,因为递归会自动修改。。。
void solve(int d[],int p[],int i,int sump,int sumd,int &min_sump)
{
//如果已经处理完,就去检查当前金币与最少金币数的比较,然后选择是否更新最小金币值。
if(i>=n)
{
if(sump<min_sump)
min_sump=sump;
return;
}
//买。。
solve(d,p,i+1,sump+p[i],sumd+d[i],min_sump);
//不买,只有当前武力值大于等于怪兽武力值时,才可以不买,因此不必每次都回溯,可以剪枝
if(sumd>=d[i])
solve(d,p,i+1,sump,sumd,min_sump);
return;
}
int main()
{
cin>>n;
int d[n];
int p[n];
for(int i=0;i<n;i++)
{
cin>>d[i];
}
for(int i=0;i<n;i++)
{
cin>>p[i];
}
int res=0;
int sump=0; //当前金币
int sumd=0; //当前武力值
int min_sump=100; //最小金币数目
solve(d,p,0,sump,sumd,min_sump);
cout<<min_sump<<endl;
return 0;
}
回溯加剪枝
题目二 矩形中的矩阵

class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param matrix char字符型vector<vector<>>
* @param word string字符串
* @return bool布尔型
*/
int m,n;
bool isFind = false;
vector<vector<bool>> isVisited;
void backTrace(vector<vector<char>>& matrix,string& word,int i,int j,int w){
if(isFind) return;
else if(w==word.size()-1) {
isFind = true;
} else{
isVisited[i][j] = true;
if(i+1<m&&!isVisited[i+1][j]&&(matrix[i+1][j]==word[w+1])){
backTrace(matrix,word,i+1,j,w+1);
}
if(i-1>=0&&!isVisited[i-1][j]&&(matrix[i-1][j]==word[w+1])){
backTrace(matrix,word,i-1,j,w+1);
}
if(j+1<n&&!isVisited[i][j+1]&&(matrix[i][j+1]==word[w+1])){
backTrace(matrix,word,i,j+1,w+1);
}
if(j-1>=0&&!isVisited[i][j-1]&&(matrix[i][j-1]==word[w+1])){
backTrace(matrix,word,i,j-1,w+1);
}
isVisited[i][j] = false;
}
}
bool hasPath(vector<vector<char> >& matrix, string word) {
// write code here
m = matrix.size();
n = matrix[0].size();
isVisited = vector<vector<bool>>(m,vector<bool>(n,false));
for(int i=0;i<m;i++){
if(isFind) break;
for(int j=0;j<n;j++){
if(isFind) break;
if(matrix[i][j]==word[0]){
backTrace(matrix,word,i,j,0);
}
}
}
return isFind;
}
};