文章目录
AM调制和DSB-SC调制都属于双边带调制,因此已调信号带宽为基带信号带宽的两倍。那么,我们有没有可能使得调制之后的信号,带宽与基带信号相同呢?这就是所谓的单边带(single sideband, SSB)调制。如图1所示,DSB-SC信号可以看作是下边带信号(LSSB)与上边带信号(USSB)的叠加。

图1 双边带信号与下边带以及上边带信号
1、滤波法产生SSB信号
那么如何产生SSB信号呢?从图1中不难看出,我们可以采用滤波的方法,从双边带信号中将下边带以及上边带信号分离出来。图(2)中(a)为SSB调制器,其中
h
S
S
B
(
t
)
h_{\rm SSB}(t)
h
S
S
B
(
t
)
可以为下边带滤波器(图b)或者上边带滤波器(图c),因此单边带信号的波形表达式为
s
S
S
B
(
t
)
=
A
c
m
(
t
)
cos
2
π
f
c
t
∗
h
S
S
B
(
t
)
,
(1)
\tag{1} s_{\rm SSB}(t)=A_cm(t)\cos 2\pi f_ct*h_{\rm SSB}(t),
s
S
S
B
(
t
)
=
A
c
m
(
t
)
cos
2
π
f
c
t
∗
h
S
S
B
(
t
)
,
(
1
)
其傅立叶变换为
S
S
S
B
(
f
)
=
A
c
2
[
M
(
f
−
f
c
)
+
M
(
f
+
f
c
)
]
H
S
S
B
(
f
)
.
(2)
\tag{2} S_{\rm SSB}(f)=\frac{A_c}{2}[M(f-f_c)+M(f+f_c)]H_{\rm SSB}(f).
S
S
S
B
(
f
)
=
2
A
c
[
M
(
f
−
f
c
)
+
M
(
f
+
f
c
)
]
H
S
S
B
(
f
)
.
(
2
)
图3为用滤波法产生下边带(图a)以及上边带(图b)信号示意图。
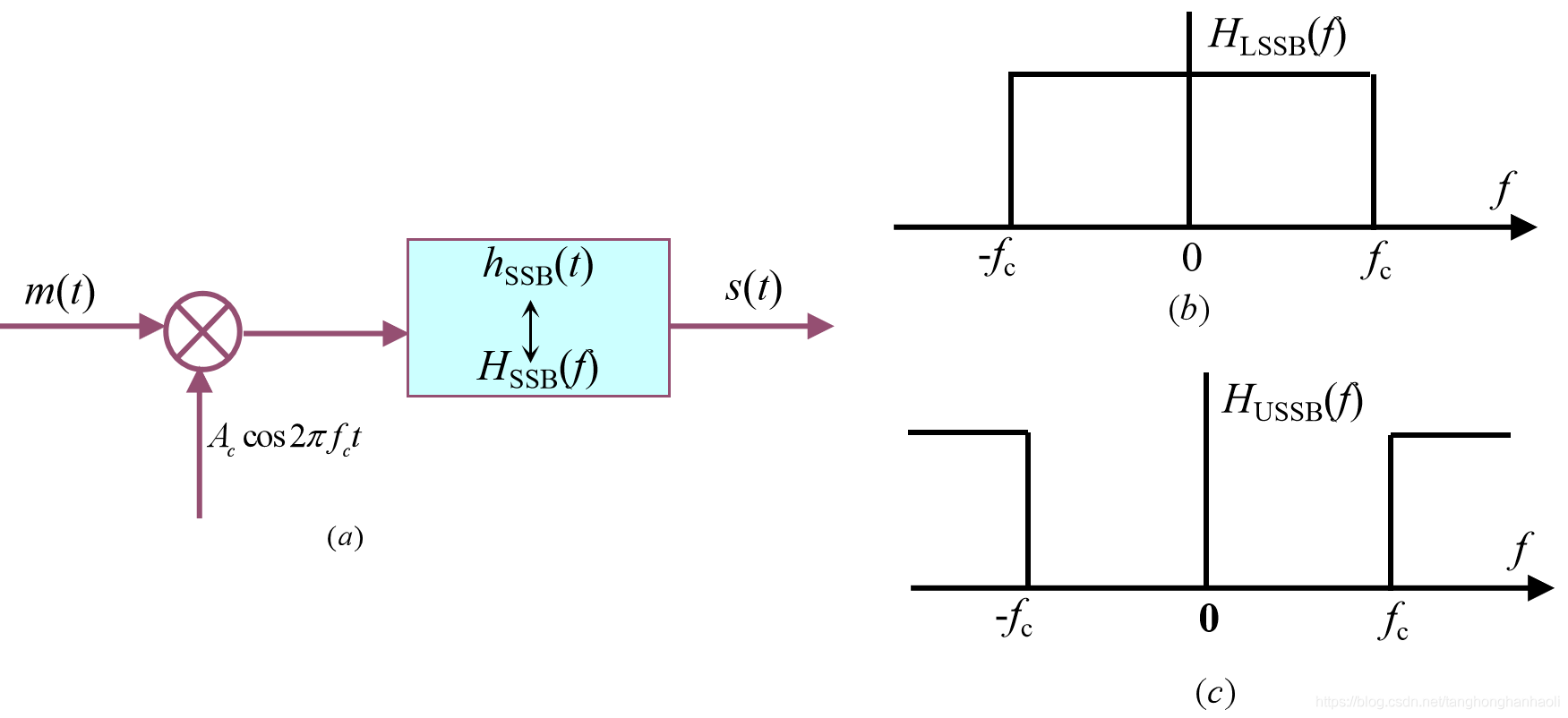
图2 SSB调制器模型

图3 滤波器产生单边带信号示意图
2、相移法产生SSB信号
显然,滤波法是从信号的频谱特性出发,从双边带信号中去掉上或者下边带频率成分,从而产生单边信号。那么是否还有其它方法可以产生单边带信号呢?
我们先来看下边带信号,图2(b)中的下边带滤波器可以表示为
H
L
S
S
B
=
1
2
[
s
g
n
(
f
+
f
c
)
−
s
g
n
(
f
−
f
c
)
]
,
(3)
\tag{3} H_{\rm LSSB}=\frac{1}{2}[{\rm sgn}(f+f_c)-{\rm sgn}(f-f_c)],
H
L
S
S
B
=
2
1
[
s
g
n
(
f
+
f
c
)
−
s
g
n
(
f
−
f
c
)
]
,
(
3
)
带入(2)得到下边带信号频谱密度为
S
L
S
S
B
(
f
)
=
A
c
2
[
M
(
f
−
f
c
)
+
M
(
f
+
f
c
)
]
H
L
S
S
B
(
f
)
=
A
c
4
[
M
(
f
−
f
c
)
+
M
(
f
+
f
c
)
]
+
A
c
4
[
M
(
f
+
f
c
)
⋅
s
g
n
(
f
+
f
c
)
−
M
(
f
−
f
c
)
⋅
s
g
n
(
f
−
f
c
)
]
.
(4)
\tag{4}\begin{aligned} S_{\rm LSSB}(f)&=\frac{A_c}{2}[M(f-f_c)+M(f+f_c)]H_{\rm LSSB}(f)\\ &=\frac{A_c}{4}[M(f-f_c)+M(f+f_c)]+\frac{A_c}{4}[M(f+f_c)\cdot {\rm sgn}(f+f_c)-M(f-f_c)\cdot {\rm sgn}(f-f_c)]. \end{aligned}
S
L
S
S
B
(
f
)
=
2
A
c
[
M
(
f
−
f
c
)
+
M
(
f
+
f
c
)
]
H
L
S
S
B
(
f
)
=
4
A
c
[
M
(
f
−
f
c
)
+
M
(
f
+
f
c
)
]
+
4
A
c
[
M
(
f
+
f
c
)
⋅
s
g
n
(
f
+
f
c
)
−
M
(
f
−
f
c
)
⋅
s
g
n
(
f
−
f
c
)
]
.
(
4
)
我们可以求得(4)的傅立叶反变换为
s
L
S
S
B
(
t
)
=
A
c
2
[
m
(
t
)
cos
2
π
f
c
t
+
m
^
(
t
)
sin
2
π
f
c
t
]
.
(5)
\tag{5} s_{\rm LSSB}(t)=\frac{A_c}{2}[m(t)\cos 2\pi f_ct+\hat m(t)\sin 2\pi f_ct].
s
L
S
S
B
(
t
)
=
2
A
c
[
m
(
t
)
cos
2
π
f
c
t
+
m
^
(
t
)
sin
2
π
f
c
t
]
.
(
5
)
同理,我们可以推得上边带信号时域表达式为
s
U
S
S
B
(
t
)
=
A
c
2
[
m
(
t
)
cos
2
π
f
c
t
−
m
^
(
t
)
sin
2
π
f
c
t
]
.
(6)
\tag{6} s_{\rm USSB}(t)=\frac{A_c}{2}[m(t)\cos 2\pi f_ct-\hat m(t)\sin 2\pi f_ct].
s
U
S
S
B
(
t
)
=
2
A
c
[
m
(
t
)
cos
2
π
f
c
t
−
m
^
(
t
)
sin
2
π
f
c
t
]
.
(
6
)
下边带信号的傅立叶变换如图4所示。从图中不难看出,
m
(
t
)
sin
2
π
f
c
t
m(t)\sin 2\pi f_ct
m
(
t
)
sin
2
π
f
c
t
是将上边带频率部分反相,与双边带信号叠加后,上边带部分被正负抵消,因而被消除掉,只保留下边带部分。
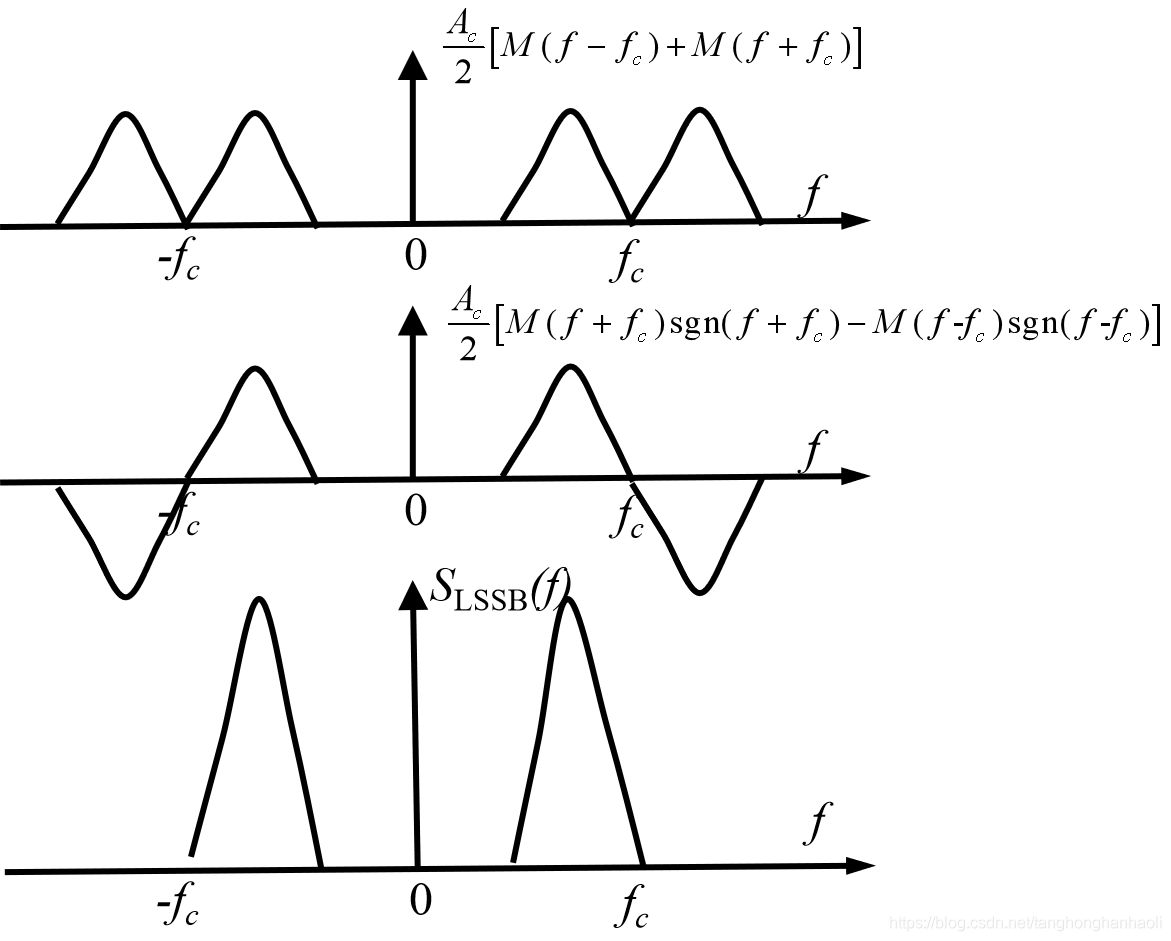
图4 相移法产生下边带信号频谱示意图
根据(5)和(6),我们可以画出相移法模型如图5所示。
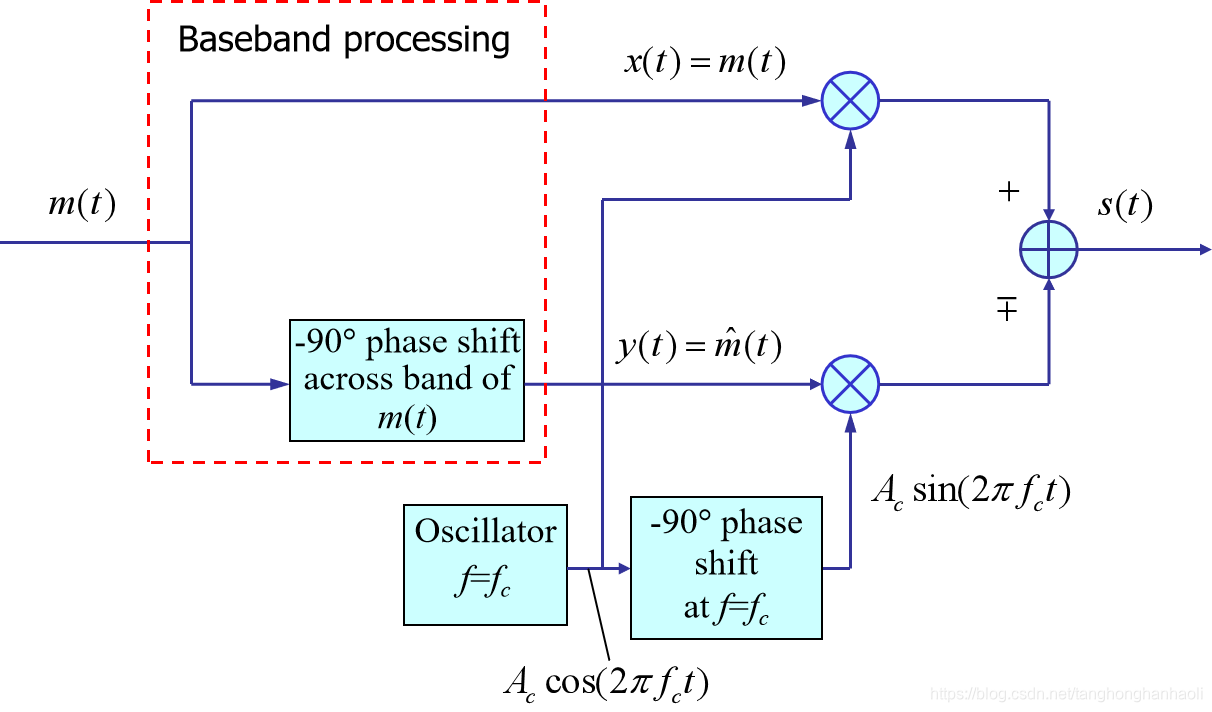
图5 相移法产生单边带信号模型