一、集成学习
AdaBoost是集成学习的一种。集成学习的目的是通过结合几个由给定的算法组成的模型,去提高单个模型的准确率。就是俗话说的三个臭皮匠顶一个诸葛亮的意思。对于多个简单的模型,集成学习有两种结合算法的方式,一种是平均的方式,例如Bagging方法,随机森林法。另一种是提升的方法,例如:Adaboost,GBDT等。
二、AdaBoost
根据上面集成学习的定义,AdaBoost算法需要回答两个问题。一个问题是在每一轮如何改变训练数据的权值,另一个问题是如何将弱分类器组合成强分类器。对于第一个问题,AdaBoost的做法是提高那些前一轮被错误分类样本的权值,降低那些被正确分类样本的权值。第二个问题,AdaBoost采取的是加权多数表决。加大分类误差率小的弱分类的权值,使其在分类中起决定性的作用。
三、AdaBoost算法过程
以李航的统计学习为例,结合例子,一步一步详细说明AdaBoost算法流程。
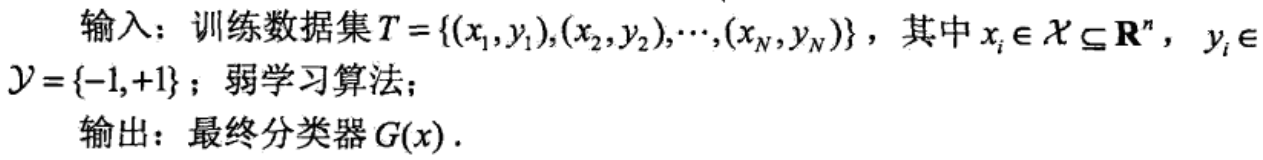
以如下训练数据为例:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |





到此第一个分类器训练完毕,然后就是训练第二个分类器,过程和第一个分类器一样,唯一不同的是,权值不再是0.1。
下面展示一下1/2*log((1-e)/e)的函数图像

可以看到,当e为0.5的时候函数值为0,当误分类的概率越小,则权重越大,否则权重越小。
四、AdaBoost算法的误差分析

五、AdaBoost算法代码实现
算法实现为GitHub源码,我阅读了源码又添加了一下注释。源代码地址为:
https://github.com/wzyonggege/statistical-learning-method
class AdaBoost:
def __init__(self, n_estimators=50, learning_rate=1.0):
#clf_num是要设置几个分类器
#learning_rate是选择最佳阈值时的间隔
self.clf_num = n_estimators
self.learning_rate = learning_rate
def init_args(self, datasets, labels):
self.X = datasets
self.Y = labels
#M为数据的个数,N为数据的特征
self.M, self.N = datasets.shape
# 弱分类器数目和集合
self.clf_sets = []
# 初始化weights,[1]*3 的结果是[1,1,1]
self.weights = [1.0/self.M]*self.M
# G(x)系数 alpha
self.alpha = []
def _G(self, features, labels, weights):
m = len(features)
error = 100000.0 # 无穷大
best_v = 0.0
# 单维features
features_min = min(features)
features_max = max(features)
n_step = (features_max - features_min + self.learning_rate) // self.learning_rate
# print('n_step:{}'.format(n_step))
direct, compare_array = None, None
#一个一个尝试,找出误分类最小的那个值
for i in range(1, int(n_step)):
v = features_min + self.learning_rate * i
if v not in features:
# 误分类计算
compare_array_positive = np.array([1 if features[k] > v else -1 for k in range(m)])
weight_error_positive = sum([weights[k] for k in range(m) if compare_array_positive[k] != labels[k]])
compare_array_nagetive = np.array([-1 if features[k] > v else 1 for k in range(m)])
weight_error_nagetive = sum([weights[k] for k in range(m) if compare_array_nagetive[k] != labels[k]])
if weight_error_positive < weight_error_nagetive:
weight_error = weight_error_positive
_compare_array = compare_array_positive
direct = 'positive'
else:
weight_error = weight_error_nagetive
_compare_array = compare_array_nagetive
direct = 'nagetive'
# print('v:{} error:{}'.format(v, weight_error))
if weight_error < error:
error = weight_error
compare_array = _compare_array
best_v = v
return best_v, direct, error, compare_array
# 计算alpha
def _alpha(self, error):
return 0.5 * np.log((1-error)/error)
# 计算规范化因子
def _Z(self, weights, a, clf):
return sum([weights[i]*np.exp(-1*a*self.Y[i]*clf[i]) for i in range(self.M)])
# 权值更新
def _w(self, a, clf, Z):
for i in range(self.M):
self.weights[i] = self.weights[i]*np.exp(-1*a*self.Y[i]*clf[i])/ Z
# G(x)的线性组合
def _f(self, alpha, clf_sets):
pass
def G(self, x, v, direct):
if direct == 'positive':
return 1 if x > v else -1
else:
return -1 if x > v else 1
def fit(self, X, y):
#初始化参数
self.init_args(X, y)
#要确定几个分类器,就要循环几次
for epoch in range(self.clf_num):
best_clf_error, best_v, clf_result = 100000, None, None
# 根据特征维度, 选择误差最小的
for j in range(self.N):
features = self.X[:, j]
# 分类阈值,分类误差,分类结果
v, direct, error, compare_array = self._G(features, self.Y, self.weights)
if error < best_clf_error:
best_clf_error = error
best_v = v
final_direct = direct
clf_result = compare_array
axis = j
# print('epoch:{}/{} feature:{} error:{} v:{}'.format(epoch, self.clf_num, j, error, best_v))
if best_clf_error == 0:
break
# 计算G(x)系数a
a = self._alpha(best_clf_error)
self.alpha.append(a)
# 记录分类器
self.clf_sets.append((axis, best_v, final_direct))
# 规范化因子
Z = self._Z(self.weights, a, clf_result)
# 权值更新
self._w(a, clf_result, Z)