支持向量机 算法
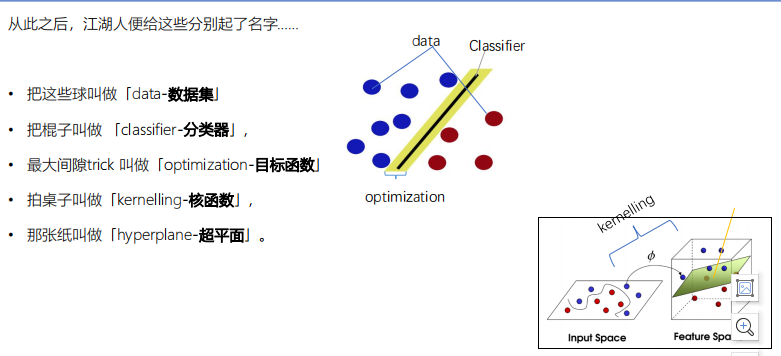
支持向量机概述
-
在机器学习领域,
SVM是一个有监督的学习模型,通常用来进行模式识别、分类以及回归分析
-
全名:Support Vector Machine(支持向量机),
支持向量是指和超平面相平行的支持平面相切的向量点
,机是指算法 -
SVM就是基于统计学习理论的一种机器学习方法,简单来说就是
将数据单元表示在多维空间中,然后对这个空间做划分的算法
-
支持向量机(Support Vector Machine, SVM)是一类按监督学习方式对数据进行
二元分类的广义线性分类器
,其决策边界是对学习样本求解的最大边距超平面。 -
SVM使用铰链损失函数计算经验风险并在求解系统中加入了正则化项以优化结构风险,是一个具有稀疏性和稳健性的分类器。
-
SVM可以通过核方法进行非线性分类,是常见的核学习方法之一。
支持向量机应用场景
-
SVM在⼿写识别数字和⼈脸识别中应⽤⼴泛
, 在⽂本和超⽂本的分类中举⾜轻重,因为SVM可以⼤量减少标准归纳和转换设 置中对标记训练实例的需求。 - 同时,SVM也被⽤来执⾏图像的分类,并⽤于 图像分割系统。实验结果表明,在仅仅三到四轮相关反馈之后,SVM就能实现⽐传统的查询细化⽅案⾼出⼀⼤截的搜索精度。
- 除此之外,⽣物学和许多其他科学都是SVM 的⻘睐者,SVM现在已经⼴泛被⽤于蛋⽩质分类,现在化合物分类的业界平均⽔平可以达到90%以上的 准确率。
支持向量机的作用
SVM用于分类,要求,在数据量增加之后,仍然适用(一般用于二分类)
支持向量机算法原理
分割超平面
- 设C和D为两个不想交的凸集,则存在超平面P,P可以将C和D分离

任意一个属于C中的数,都很高小于等于b,任意一个属于D中的数,都能大于等于b
-
两个集合的距离,定义为两个集合间元素的最短距离
-
做集合C和集合D最短线段的垂直平分线,中间的垂直线就是分类器
<
分割超平面的思考
-
如何定义两个集合的“最优”分割超平面?
- 找到集合“边界”上的若干点,以这些点为“基础”计算超平面的方向;以两个集合边界上的这些点的平均作为超平面的“截距”。
- 支持向量:support vector
-
若两个集合有部分相交,如何定义超平面,使得两个集合“尽量”分开?

输入数据
- 假设给定一个特征空间上的训练数据集

-
Xi为第i个实例(若n>1,Xi为向量 )
-
Yi为Xi的类标记
- 当Yi=+1时,称Xi为正例
- 当Yi=-1时,称Xi为负例;
-
(Xi, Yi)称为样本点
-
给定线性可分训练数据集,通过间隔最大化得到的分离超平面为:


如果y(x)算出来是大于0的,就把它当作y=+1类,如果y(x)算出来小于0,就把它当作y=-1类
-

是某个确定的特征空间转换函数,它的作用是将X映射到(更高的)维度
最简单直接的:


整理的符号(了解)
- 分割平面

- 训练集

- 目标值:

- 新数据的分类:sign函数是指示函数【当wx+b > 0,f(x) = +1;当wx+b < 0,f(x) =-1】

支持向量机-线性可分(知道)
-
最优超平面可以定义为: ?? * x + b = 0
-
w : 是权重向量,1*N的维度,W={w1,w2,…,wn},n是特征值个数。
-
X是训练实例,与w相对应是N*1的维度,X有多少维,W就有多少维
-
b:bias,偏向偏好
-
-
紧贴支撑向量的两条超平面,我们将其定义分别定义为:
- ?? * x + b = 1
- ?? * x + b = -1
-
定义一个分类函数:f(x)= ?? * x + b
- 当f(x)=0 ,那么 x 是位于超平面上的点
- 当f(x)>0时,就把它归到y=+1那一类
- 当f(x)<0时,就把它归到y=-1那一类
支持向量机-线性不可分
有时候会出现以下这种情况,用直线不管怎么分都分不好,需要用到曲线去分,这种就是线性不可分
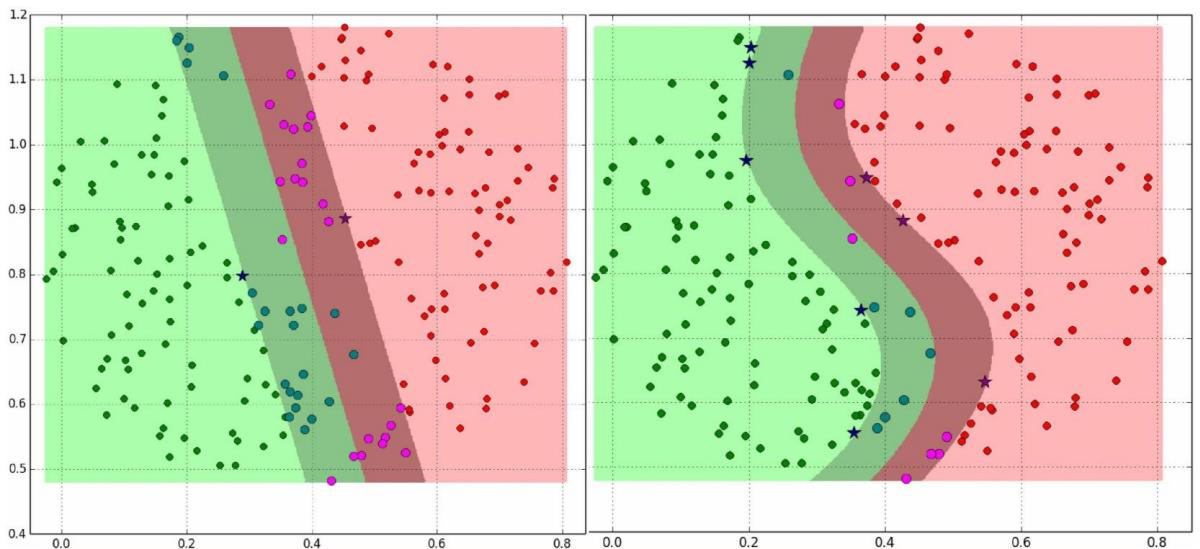
- 使用“核函数”解决线性不可分
-
可以使用核函数,
对数据进行升维,将原始输入空间映射到新的特征空间
,从而,是的原本线性不可分的样本可能在核空间可分
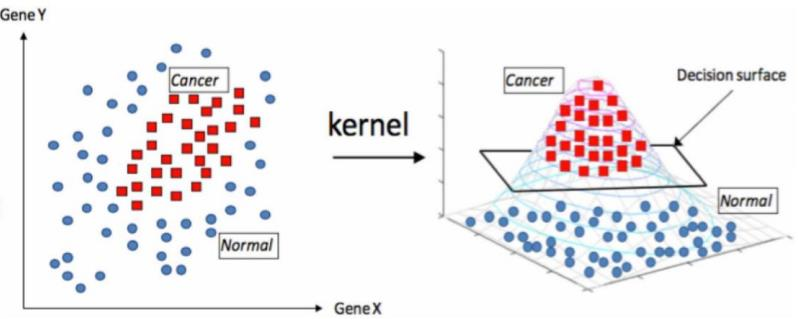
常见的核函数(熟悉)

实战经验
:没有更多的先验信息,则使用
径向基核函数(高斯核函数)
。
推导目标函数(重点)
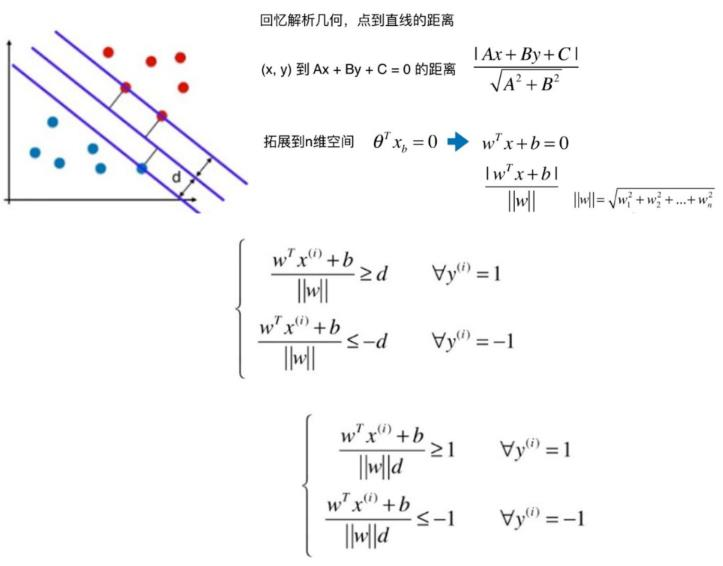
|wx+b| / ||w|| >=d (距离要大于等于d)
-
y属于+1这个类, y=+1, 只有在wx+b为正的时候才会归为这类,那么wx+b在算对的情况下,一定属于整数,正数的绝对值也属于正数 , |wx+b|就等于wx+b本身, wx+b / ||w|| 也会大于等于d
-
y属于-1这个类, y=-1, wx+b就<=0,在wx+b算对的情况下, -(wx+b)/||w||>=d, 想将-号转移到右边去,则两边同乘一个-号,判断符号就要转向,原本的-(wx+b)/||w||>=d 就变成 (wx+b)/||w||<= -d
算式与值两边同除以一个d,就变成最后那个公式,等号后面就变成1和-1
(wx+b) /||w||b 可以变成每个数缩小||w||d这么多倍,就变成下面的内容


最大间隔分离超平面



函数间隔和几何间隔



求
新目标函数
,就是求
min||w||
,
min||w||
等价于
min||w||^2
等价于
min 0.5*||w||^2
建立目标函数

求解目标函数
-
目标函数是凸函数,而且是二次形式
-
约束是线性的
对于复杂情况,需要转换为“对偶问题”(对偶函数与原函数等价)
支持向量机算法原理总结-线性不可分★
目标函数(松弛变量):

支持向量机优缺点
优点:
- 可以解决高维问题,即大型特征空间
-
能够处理非线性特征的相互作用
- 无局部极小值问题(相对于神经网络等算法)
- 无需依赖整个数据
- 泛化能力比较强
缺点:
-
当观测样本很多时,
效率并不是很高
-
对非线性问题没有通用解决方案,
有时候很难找到一个合适的核函数
- 对于核函数的高维映射解释力不强,尤其是径向基函数
- 常规SVM只支持二分类
- 对缺失数据敏感
支持向量机代码实现
导入模块
from sklearn.svm import SVC
建立模型
clf = SVC().fit(X, y)
参数介绍
class sklearn.svm.SVC(*, C=1.0, kernel='rbf', degree=3,
gamma='scale', coef0=0.0, shrinking=True,
probability=False, tol=0.001, cache_size=200,
class_weight=None, verbose=False, max_iter=- 1,
decision_function_shape='ovr',
break_ties=False, random_state=None)
重点参数:
-
kernel: 字符,可不填,默认’rbf’,指定要在算法中使用的核函数类型,可以输入’linear ‘, ‘poly , ‘rbf , ‘sigmoid’,’precomputed”或者可调用对象(如函数,类等)。如果给出可调用对象,则这个对象将被用于从特征矩阵X预先计算内核矩阵;该矩阵应该是是一个(n_samples, n_samples)结构的数组。
- 参数degree(核函数)一点补充说明:
-

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
iris = datasets.load_iris()
x = iris['data']
y = iris['target']
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)
m1 = SVC(kernel='linear').fit(X_train, y_train)
m2 = SVC(kernel='sigmoid').fit(X_train, y_train)
m3 = SVC(kernel='rbf').fit(X_train, y_train)
m4 = SVC(kernel='poly').fit(X_train, y_train)
m1.predict(X_test)
y_test
m1.score(X_test, y_test)
m2.score(X_test, y_test)
m3.score(X_test, y_test)
m4.score(X_test, y_test)
y_train)
m2 = SVC(kernel=‘sigmoid’).fit(X_train, y_train)
m3 = SVC(kernel=‘rbf’).fit(X_train, y_train)
m4 = SVC(kernel=‘poly’).fit(X_train, y_train)
m1.predict(X_test)
y_test
m1.score(X_test, y_test)
m2.score(X_test, y_test)
m3.score(X_test, y_test)
m4.score(X_test, y_test)