3D计算机视觉,图形学,机器人学的研究经常涉及三维旋转的估计 。这里分享一篇CVPR19的论文“On the Continuity of Rotation Representations in Neural Networks”。这篇文章分析比较了旋转矩阵,欧拉角,四元数等常见三维旋转表示对神经网络训练的影响,并提出了一种适合深度学习的
三维旋转表示方法。
不连续(Continiuous)的旋转表示不是好的旋转表示
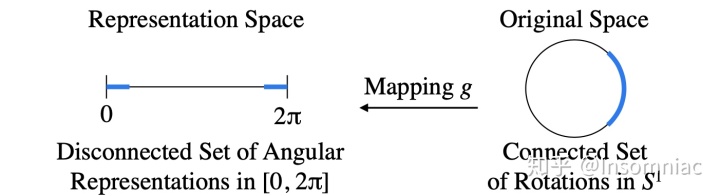
文章提供了简单的2D旋转的例子:某旋转矩阵
可以以一个角度
表示,假设映射
的作用是实现这一转换
,图示在旋转矩阵的空间中某一连通集在经过这个映射后变成了不连通集。文章argue,这种旋转表示会造成监督信号的不连续,因此不利于神经网络学习。
三维旋转表示的连续性的定义

假设在深度学习中,某一神经网络学得某一表征空间
中的三维旋转表示,而旋转矩阵
所在的空间为原空间
,它们之间的正反映射分别为
和
,那么文章定义如果
是连续的,则这个三维旋转表征就是连续的。根据这个定义,
欧拉角(Euler Angles),轴角(Axis-Angle)和四元数(Quaternions)都不是连续的旋转表示
,具体分析请参看论文。
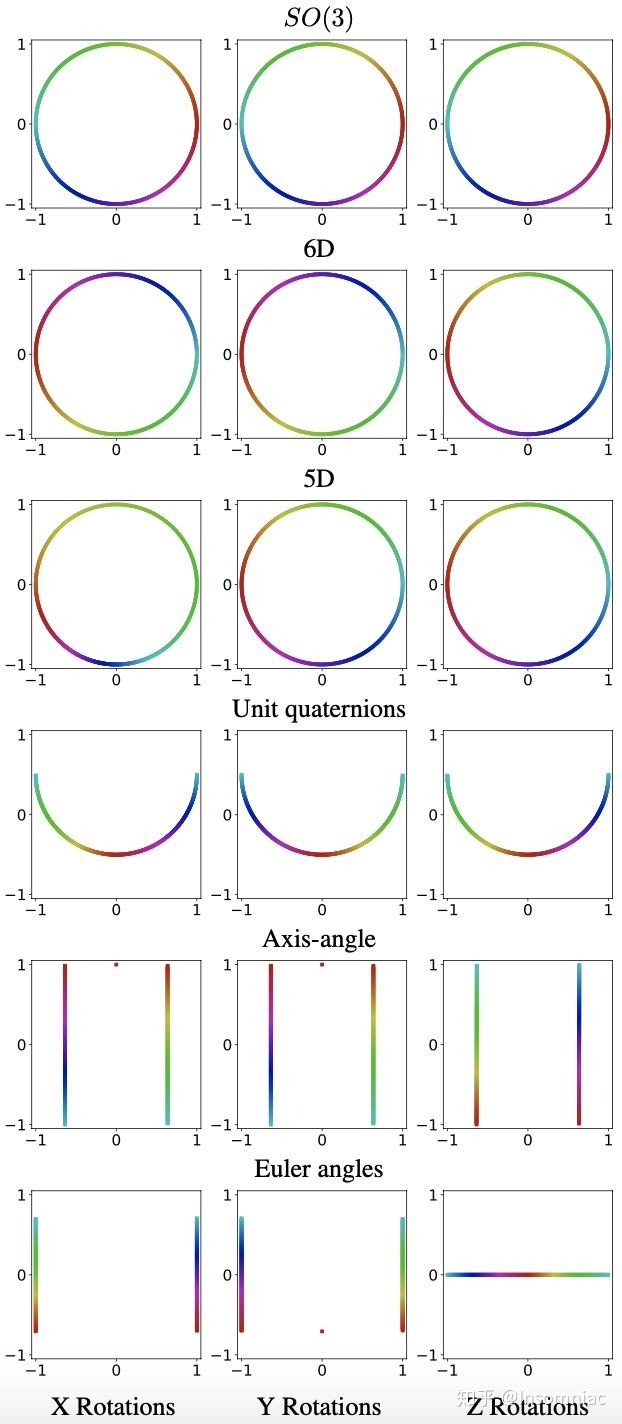
连续的
三维旋转表示
旋转矩阵是一种连续的三维旋转表示,那么自然想到可以用神经网络来直接regress旋转矩阵,这里假设神经网络的输出为
。由于神经网络的输出
并不一定是orthonormal且行列式等于
的,也就是说
不一定成立,因此自然想到可以对
进行 Gram-Schmidt 正交化。假设
中的三个列向量:
,那么Gram-Schmidt会给我们一个矩阵
,其中
这里的
代表向量
在向量
上的投影,
是将向量normalize成单位向量。Gram-Schmidt正交化保证了得到的
是orthonormal 的,但仍不一定满足
。实际上,如果观察 Gram-Schmidt 正交化的过程,会发现
仅仅决定了
的正负号,而
的方向是可以通过
来决定的,而也正是因为
决定了
的正负号,导致
的行列式不一定为
。所以,
其实是不必要的。
所以文章提出的
表征也就也就是用让神经网络regress两个向量
和
,将这两个向量正交化后,通过叉乘确定第三个向量,这样就保证了最终得到的
。

对于这种旋转表示,
函数仅仅是丢掉矩阵的最后一个列向量,因此是连续的。
实验结果
5D和6D是文章所提出的新的连续的旋转表示。
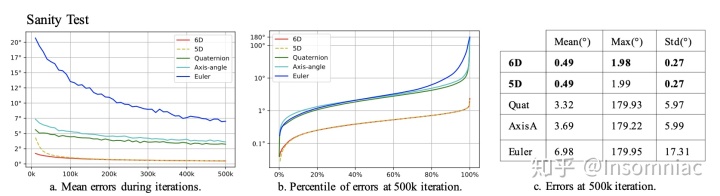
Sanity Test 就是一个简单的Reconstruction任务,训练一个神经网络自动编码器(Autoencoder)来把旋转矩阵编码为某种表示
再还原为旋转矩阵。
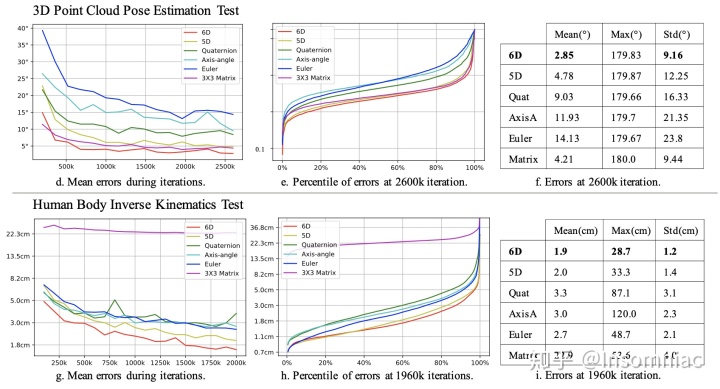
3D点云姿态估计和人体Inverse Kinematics的结果。需要注意的是,表 f 中的 Matrix 是用神经网络直接regress旋转矩阵再用 Gram-Schmidt 正交化之后的结果,而表 g 中的 Matrix 没有进行Gram-Schmidt 正交化。
论文原文:Zhou, Yi, et al. “On the continuity of rotation representations in neural networks.”
Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition
. 2019.
http://openaccess.thecvf.com/content_CVPR_2019/papers/Zhou_On_the_Continuity_of_Rotation_Representations_in_Neural_Networks_CVPR_2019_paper.pdfopenaccess.thecvf.com