
CNN经过一些简单的调整就可以成为序列建模和预测的强大工具
尽管卷积神经网络(CNNs)通常与图像分类任务相关,但经过适当的修改,它已被证明是进行序列建模和预测的有价值的工具。在本文中,我们将详细探讨时域卷积网络(TCN)所包含的基本构建块,以及它们如何结合在一起创建一个强大的预测模型。使用我们的开源Darts TCN实现,我们展示了只用几行代码就可以在真实数据集上实现准确预测。
以下对时间卷积网络的描述基于以下论文:https://arxiv.org/pdf/1803.01271.pdf。本文引用用(*)表示。
动机
到目前为止,深度学习背景下的序列建模主题主要与递归神经网络架构(如LSTM和GRU)有关。S. Bai等人(*)认为,这种思维方式已经过时,在对序列数据进行建模时,应该将卷积网络作为主要候选者之一加以考虑。他们能够表明,在许多任务中,卷积网络可以取得比RNNs更好的性能,同时避免了递归模型的常见缺陷,如梯度爆炸/消失问题或缺乏内存保留。此外,使用卷积网络而不是递归网络可以提高性能,因为它允许并行计算输出。他们提出的架构称为时间卷积网络(TCN),将在下面的部分中进行解释。为了便于理解TCN体系结构及其Darts实现,本文将尽可能使用与库中看到的相同的模型参数名称。
基本模型
概述
TCN是时域卷积网络(Temporal Convolutional Network)的简称,它由具有相同输入和输出长度的扩张的、因果的1D卷积层组成。下面几节将详细介绍这些术语的实际含义。
一维卷积网络
一维卷积网络以一个三维张量作为输入,也输出一个三维张量。我们的TCN实现的输入张量具有形状(batch
size、input
length、input
size),输出张量具有形状(batch
size、input
length、output
size)。由于TCN中的每一层都有相同的输入和输出长度,所以只有输入和输出张量的第三维是不同的。在单变量情况下,input
size和output
size都等于1。在更一般的多变量情况下,input
size和output
size可能不同,因为我们可能不希望预测输入序列的每个组件。
单个1D卷积层接收一个shape的输入张量(batch
size, input
length, nr
input
channels)并输出一个shape张量(batch
size, input
length, nr
output
channels)。为了了解单个层如何将其输入转换为输出,让我们看一下批处理的一个元素(对批处理中的每个元素都进行相同的处理)。让我们从最简单的例子开始,其中nr
input
channels和nr
output
channels都等于1。在这种情况下,我们看到的是一维输入和输出张量。下图显示了输出张量的一个元素是如何计算的。
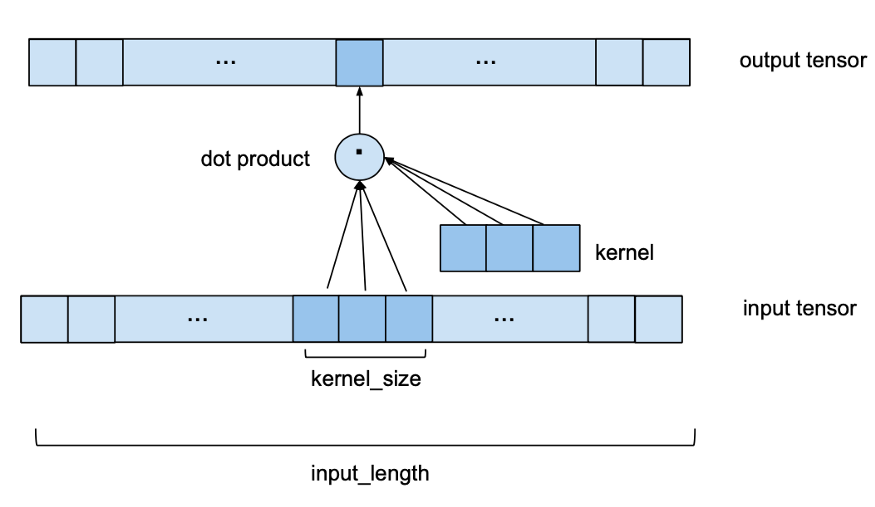
我们可以看到,要计算输出的一个元素,我们需要查看输入的一系列长度为kernel
size的连续元素。在上面的例子中,我们选择了一个3的kernel
size。为了得到输出,我们取输入的子序列和相同长度的已学习权值的核向量的点积。输出的下一个元素,相同的应用程序,但kernel_size-sized窗口的输入序列是由一个元素转移到正确的(对于本预测模型,stride 总是设置为1)。请注意,相同的一组内核权重将被用来计算每输出一个卷积层。下图显示了两个连续的输出元素及其各自的输入子序列。
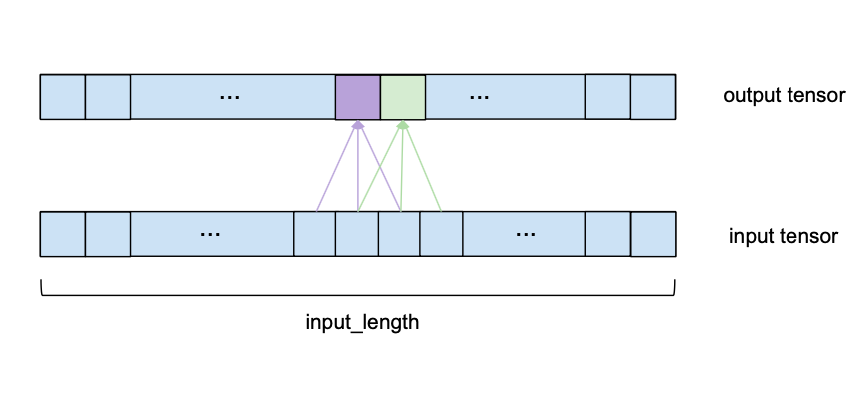
为了使可视化更简单,与核向量的点积不再显示,而是对每个具有相同核权重的输出元素发生。
为了确保输出序列与输入序列具有相同的长度,将应用一些零填充。这意味着在输入张量的开始或结束处添加额外的零值项,以确保输出具有所需的长度。后面的部分将详细解释如何做到这一点。
现在让我们看看有多个输入通道的情况,即nr
input
channels大于1。在本例中,上述过程对每个单独的输入通道都重复,但每次都使用不同的内核。这将导致nr
input
channels中间输出向量和kernel
size * nr
input
channels的一些内核权重。然后将所有中间输出向量相加,得到最终输出向量。在某种意义上,这相当于与一个形状的输入张量(input
size, nr
input
channels)和一个形状的内核张量(kernel
size, nr
input_channels)进行2D卷积,如下图所示。它仍然是一维的因为窗口只沿着一个轴移动,但是我们在每一步都有一个二维卷积因为我们使用的是一个二维核矩阵。
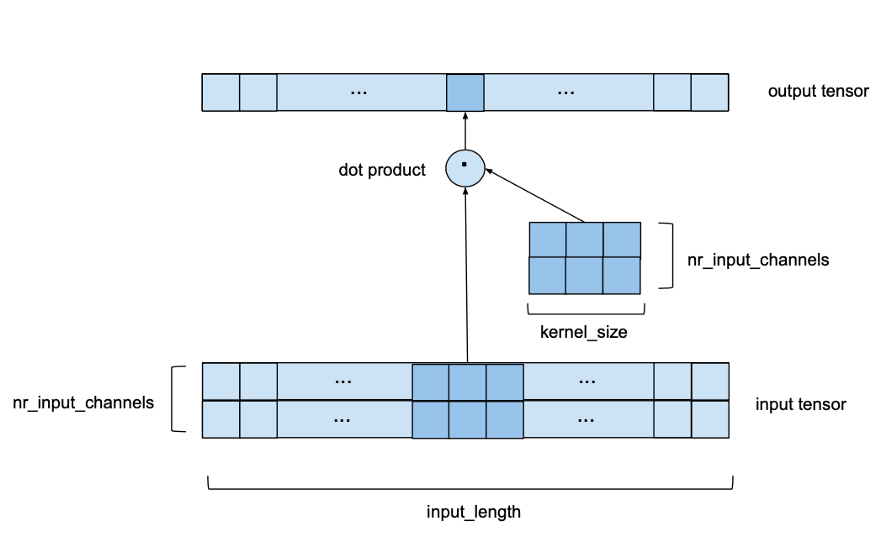
对于本例,我们选择nr
input
channels等于2。现在,我们使用nr
input
channels by kernel
size内核矩阵沿着nr
input
channels宽系列长度input
length来代替在一维输入序列上滑动的核向量。
如果nr
input
channels和nr
output
channels都大于1,那么对每个具有不同内核矩阵的输出通道重复上述过程。然后将输出向量堆叠在一起,得到一个形状的输出张量(input
length, nr
output
channels)。本例中的内核权重数等于kernel
size
nrinputchannels
nr
output
channels。
nr
input
channels和nr
output
channels这两个变量取决于该层在网络中的位置。第一层是nr
input
channels = input
size,最后一层是nr
output
channels = output
size。所有其他层将使用由num_filters提供的中间通道号。
因果卷积
对于因果关系,对于{0,…,input
length – 1}中的每一个i,输出序列的第i个元素可能只依赖于索引为{0,…,i}的输入序列中的元素。换句话说,输出序列中的元素只能依赖于输入序列中在它之前的元素。如前所述,为了确保一个输出张量与输入张量具有相同的长度,我们需要进行零填充。如果我们只在输入张量的左侧填充零,那么就可以保证因果卷积。要理解这一点,请考虑最右边的输出元素。假设输入序列的右边没有填充,它所依赖的最后一个元素就是输入的最后一个元素。现在考虑输出序列中倒数第二个输出元素。与最后一个输出元素相比,它的内核窗口向左移动了1,这意味着它在输入序列中最右边的依赖项是输入序列中倒数第二个元素。根据归纳,对于输出序列中的每个元素,其在输入序列中的最新依赖项与其本身具有相同的索引。下图展示了一个input
length为4,kernel_size为3的示例。
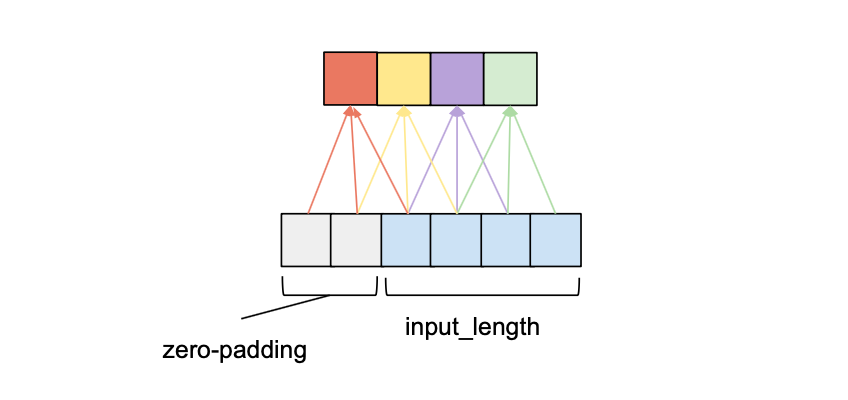
我们可以看到,在两个条目的左填充为零的情况下,我们可以获得相同的输出长度,同时遵守因果关系规则。事实上,在没有扩展的情况下,维持输入长度所需的零填充条目的数量总是等于kernel_size – 1。
扩张
预测模型的一种理想质量是输出中特定条目的值取决于输入中所有先前的条目,即索引小于或等于其自身的所有条目。当接受野(指影响输出的特定条目的原始输入的一组条目)的大小为input
length时,就可以实现这一点。我们也称其为“完整的历史记录”。正如我们以前看到的,一个传统的卷积层在输出中创建一个依赖于输入的kernel
size项的条目,这些条目的索引小于或等于它自己。例如,如果我们的kernel
size为3,那么输出中的第5个元素将依赖于输入中的元素3、4和5。当我们将多个层叠加在一起时,这个范围就会扩大。在下面的图中我们可以看到,通过kernel
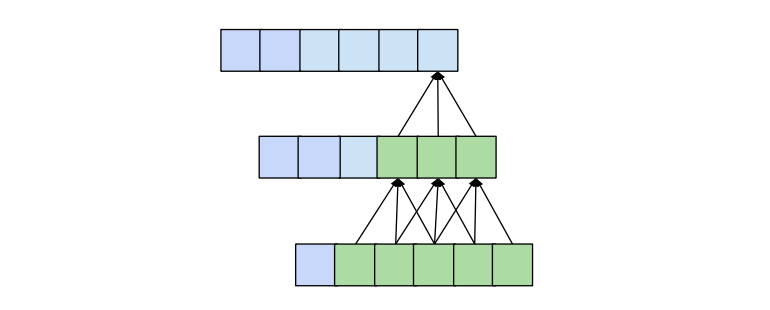
size 3叠加两层,我们得到的接受野大小为5。
一般而言,具有n层且kernel_size为k的一维卷积网络的接收场r为
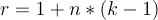
为了知道需要多少层才能完全覆盖,我们可以将接受野大小设为input_length l,然后求解层数n(非整数值需要进行四舍五入):
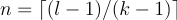
这意味着,kernel_size固定,完整的历史覆盖所需的层数是线性的输入长度的张量,这将导致网络变得非常深非常快,导致模型与大量的参数,需要更长的时间来训练。此外,大量的层已被证明会导致与损失函数梯度相关的退化问题。在保持层数相对较小的情况下,增加感受野大小的一种方法是向卷积网络引入膨胀概念。
卷积层上下文中的膨胀是指输入序列的元素之间的距离,该元素用于计算输出序列的一个条目。 因此,传统的卷积层可以看作是dilated为1的扩散层,因为1个输出值的输入元素是相邻的。 下图显示了一个dilated为2的扩散层的示例,其input
length为4,kernel
size为3。

与dilated-1扩散的情况相比,该层的接收场沿5而不是3的长度扩展。更普遍地,具有内核大小k的d扩散层的接收场沿1 + d的长度扩展。 *(k-1)。 如果d是固定的,那么仍然需要输入张量的长度为线性的数字才能实现完全的接收场覆盖(我们只是减小了常数)。
这个问题可以通过在层中向上移动时d的值呈指数增加来解决。 为此,我们选择一个常数dilation
base整数b,它将使我们根据其下的层数i来计算特定层的膨胀d,即d = b ** i。 下图显示了一个网络,其中input
length为10,kernel
size为3,dilation
base为2,这将导致3个膨胀的卷积层完全覆盖。
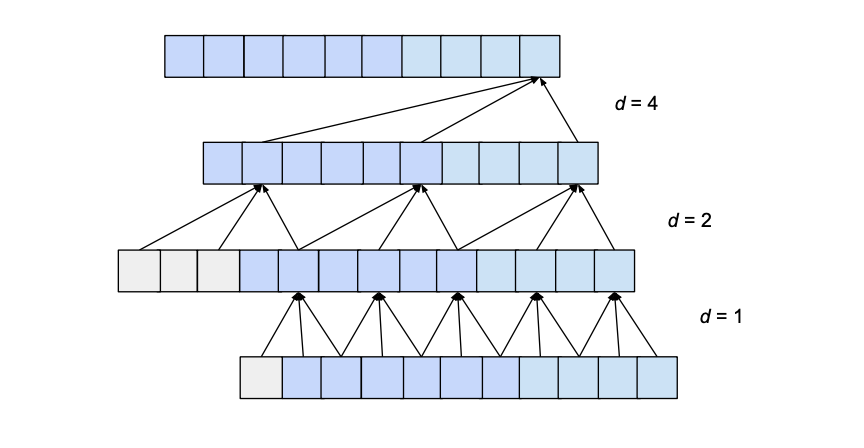
这里我们只显示影响输出最后一个值的输入的影响。同样,只显示最后一个输出值所必需的补零项。显然,最后的输出值依赖于整个输入覆盖率。实际上,给定超参数,input_length最多可以使用15,同时保持完全的接收野覆盖。一般来说,每增加一层,当前接受野宽度就增加一个d*(k-1)值,其中d计算为d=b**i, i表示新层下面的层数。因此,给出了基b指数膨胀时TCN的感受场宽度w、核大小k和层数n为
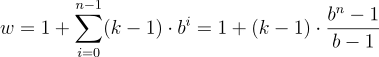
然而,根据b和k的值,这个接受野可能会有“洞”。考虑以下网络,其dilation_base为3,内核大小为2:
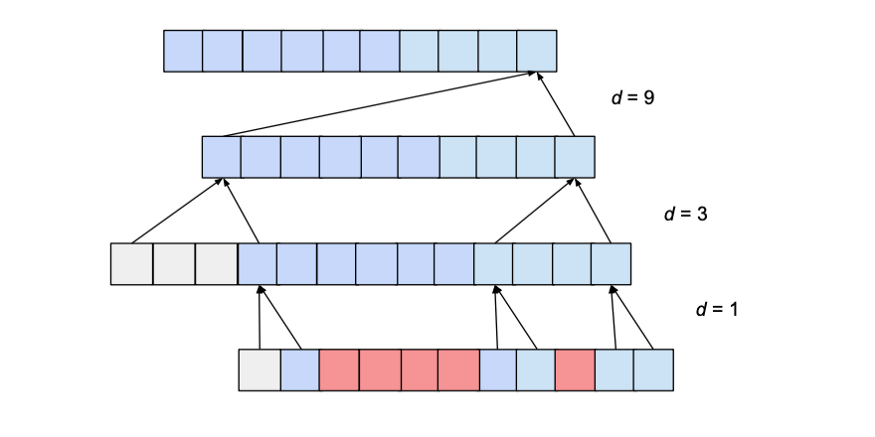
接受野的范围确实大于输入的大小(即15)。然而,接受野是有洞的;也就是说,在输入序列中有输出值不依赖的条目(如上面红色所示)。为了解决这个问题,我们需要将内核大小增加到3,或者将膨胀基数减小到2。一般来说,对于没有孔的感受野,核的大小k至少要与膨胀基b一样大。
考虑到这些观察结果,我们可以计算出我们的网络需要多少层才能覆盖整个历史。给定核大小k,膨胀基b,其中k≥b,输入长度l,为了实现全历史覆盖,必须满足以下不等式:
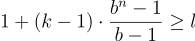
我们可以求解n,得到所需的最小层数
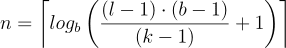
我们可以看到,在输入长度方面,层数现在是对数的,而不是线性的。这是一个显著的改进,可以在不牺牲接受野覆盖率的情况下实现。
现在,唯一需要指定的是每一层所需的零填充项的数量。假设膨胀基为b,核大小为k,当前层以下有i个层,则当前层所需的补零项数p计算如下:
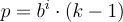
基本TCN概述
给定input
length, kernel
size, dilation_base和覆盖整个历史所需的最小层数,基本的TCN网络看起来像这样:
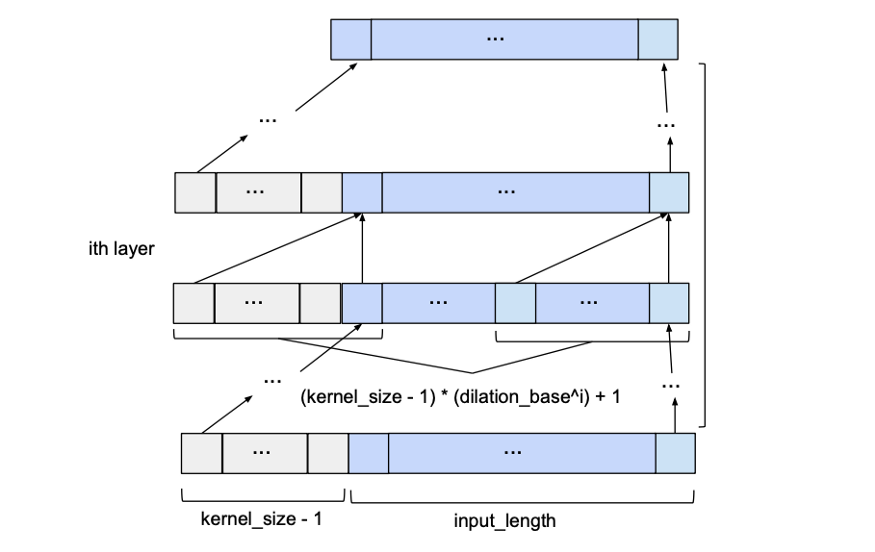
预测
到目前为止,我们只讨论了‘输入序列’和‘输出序列’,而没有深入了解它们之间是如何相互关联的。在预测方面,我们希望预测未来时间序列的下一个条目。为了训练我们的TCN网络进行预测,训练集将由给定时间序列的等大小子序列对(输入序列、目标序列)组成。目标序列将是相对于其各自的输入序列向前移动一定数量output
length的序列。这意味着长度input
length的目标序列包含其各自输入序列的最后(input
length – output
length)元素作为第一个元素,位于输入序列最后一个条目之后的output
length元素作为它的最后一个元素。在预测方面,这意味着该模型所能预测的最大预测视界等于output
length。使用滑动窗口的方法,许多重叠的输入和目标序列可以创建出一个时间序列。
模型的改进
S. Bai等人(*)建议对基本的TCN体系结构进行一些添加,以提高本节将讨论的性能,即残差连接、正则化和激活函数。
残差块
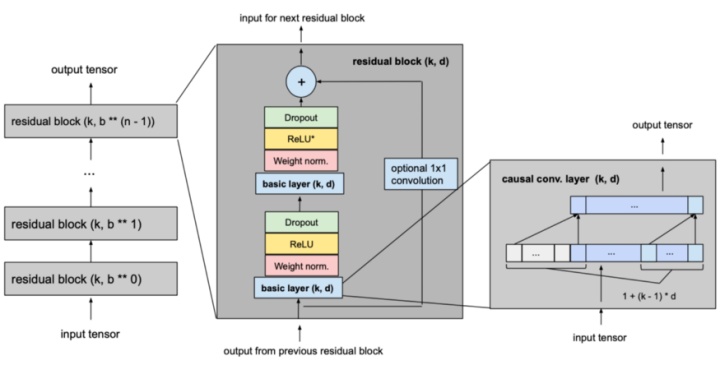
我们对之前介绍的基本模型做的最大的修改是将模型的基本构建块从简单的一维因果卷积层改为由相同膨胀因子和残差连接的2层组成的残差块。
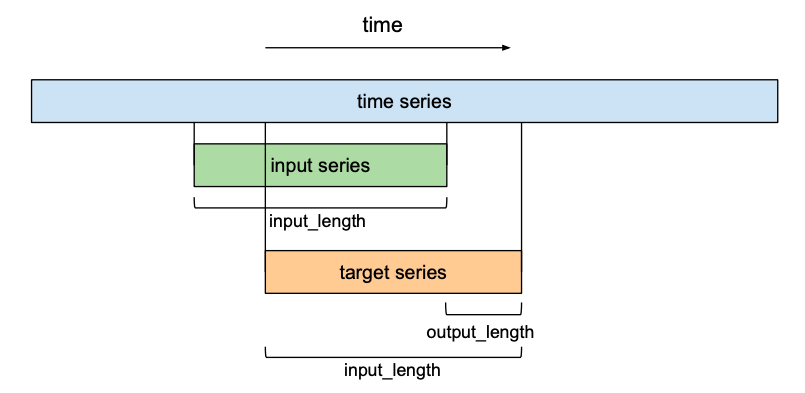
让我们从基本模型中考虑一个膨胀系数d为2、内核大小k为3的层,看看这是如何转化为改进模型的剩余块的。
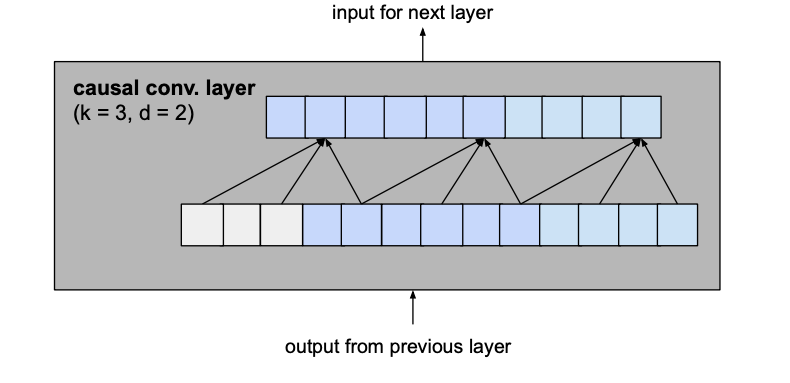
变为
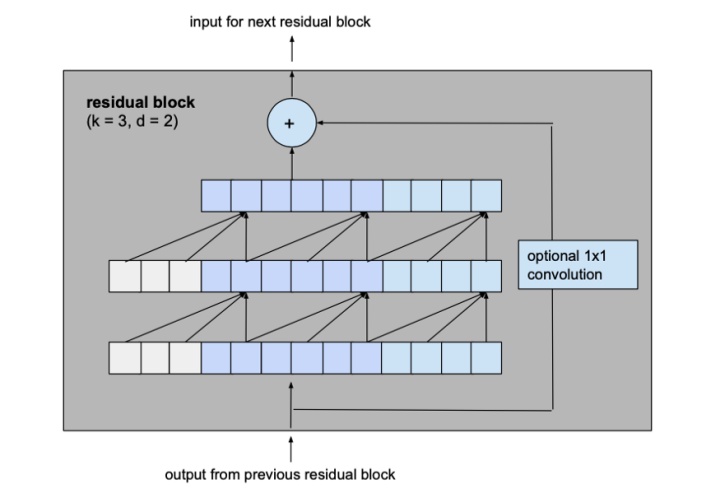
这两个卷积层的输出将被添加到残差块的输入中,从而产生下一个块的输入。对于网络的所有内部块,即除了第一个和最后一个之外的所有内部块,输入和输出通道宽度是相同的,即num_filters。由于第一个残块的第一卷积层和最后一个残块的第二卷积层可能有不同的输入和输出通道宽度,所以可能需要调整残差张量的宽度,这是通过1×1卷积来完成的
此更改会影响对完整覆盖所需的最小层数的计算。现在我们必须考虑需要多少残差块才能实现接收域的完全覆盖。在TCN中添加一个残差块所增加的接受野宽度是添加一个基本因果层时的两倍,因为它包含两个这样的层。因此,扩张基为b的TCN的感受场总大小r、k≥b的核大小k和剩余块数n可计算为
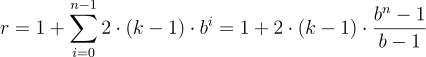
这保证了最小的残差块数n为input_length l的完整历史覆盖
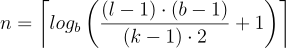
激活,规范化、正规化
为了使我们的TCN不仅仅是一个过于复杂的线性回归模型,需要在卷积层的顶部添加激活函数来引入非线性。ReLU激活被添加到两个卷积层之后的残差块中。
为了规范化隐含层的输入(抵消了梯度爆发的问题),权值规范化应用于每一个卷积层。
为了防止过拟合,在每个剩余块的每个卷积层之后通过dropout引入正则化。下图显示了最终的剩余块。
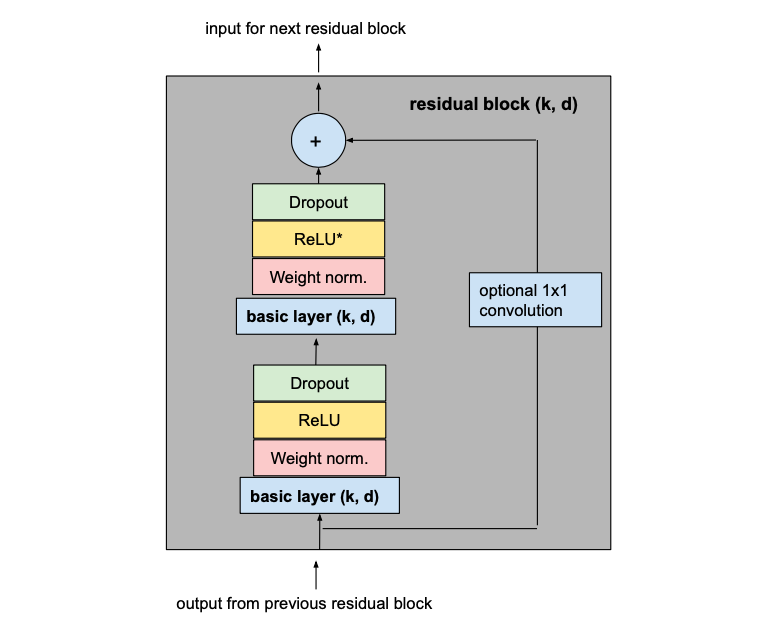
第二个ReLU单元中的星号表示该层存在于除最后一层之外的所有层中,因为我们希望最终输出也能够具有负值(这与本文中概述的体系结构不同)。
模型
下图显示了我们最终的TCN模型,其中l等于input
length,k等于kernel
size,b等于dilation_base,k≥b,并且对于完整的历史覆盖n为最小数量的残差块,其中n可以从其他值计算得出 如上所述。
示例
让我们看一个示例,该示例说明如何使用Darts库使用TCN架构预测时间序列。
首先,我们需要一个时间序列来训练和评估我们的模型。 为此,我们使用了Kaggle数据集,其中包含来自西班牙的每小时能源生产数据。 更具体地说,我们选择预测“河流上游水电”的产量。 此外,为了使问题的计算量减少,我们将每天的平均能源生产量取平均以获得每日的时间序列。
from darts import TimeSeries
from darts.dataprocessing.transformers import MissingValuesFiller
import pandas as pddf = pd.read_csv(‘energy_dataset.csv’, delimiter=”,”)
df[‘time’] = pd.to_datetime(df[‘time’], utc=True)
df[‘time’]= df.time.dt.tz_localize(None)df_day_avg = df.groupby(df[‘time’].astype(str).str.split(” “).str[0]).mean().reset_index()value_filler = MissingValuesFiller()
series = value_filler.transform(TimeSeries.from_dataframe(df_day_avg, ‘time’, [‘generation hydro run-of-river and poundage’]))series.plot()
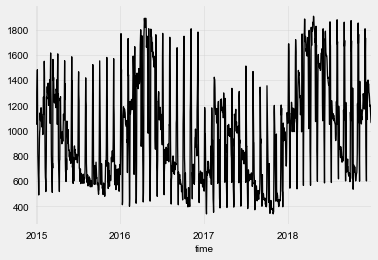
我们可以看到,除了每年的季节性之外,每月还会定期出现能源生产中的“峰值”。 由于TCN模型支持多个输入通道,因此我们可以在当前时间序列中添加其他时间序列分量,以对当月的当前日期进行编码。 这可以帮助我们的TCN模型更快地收敛。
series = series.add_datetime_attribute(‘day’, one_hot=True)
现在,我们将数据分为训练和验证组件并执行标准化。
from darts.dataprocessing.transformers import Scalertrain, val = series.split_after(pd.Timestamp(‘20170901’))scaler = Scaler()
train_transformed = scaler.fit_transform(train)
val_transformed = scaler.transform(val)
series_transformed = scaler.transform(series)
现在是时候创建和训练我们的TCN模型了。 注意,上面对体系结构的描述中出现的所有变量名都可以用作Darts TCN实现的构造函数的参数。 由于我们要执行每周预测,因此output
length参数设置为7。 在训练模型时,我们仅将训练系列的第一部分指定为target
series,因为我们不想预测我们之前添加的助手时间序列。 我们尝试了几种不同的超参数组合,但是大多数值是任意选择的。
from darts.models import TCNModelmodel = TCNModel(
input_size=train.width,
n_epochs=20,
input_length=365,
output_length=7,
dropout=0,
dilation_base=2,
weight_norm=True,
kernel_size=7,
num_filters=4,
random_state=0
)model.fit(
training_series=train_transformed,
target_series=train_transformed[‘0’],
val_training_series=val_transformed,
val_target_series=val_transformed[‘0’], verbose=True
)
为了评估我们的模型,我们希望使用7天的预测范围在验证集中的许多不同时间点测试其性能。 为此,我们使用了Darts的历史回测功能。 请注意,该模型为每个前提提供了新的输入数据,但从未对其进行过重新训练。 为了节省时间,我们将跨度设置为5。
pred_series = model.backtest(
series_transformed,
target_series=series_transformed[‘0’],
start=pd.Timestamp(‘20170901’),
forecast_horizon=7,
stride=5,
retrain=False,
verbose=True,
use_full_output_length=True
)
让我们根据地面真实数据点将TCN模型的历史预测预测可视化,并计算R2得分。
from darts.metrics import r2_score
import matplotlib.pyplot as pltseries_transformed[900:][‘0′].plot(label=’actual’)
pred_series.plot(label=(‘historic 7 day forecasts’))
r2_score_value = r2_score(series_transformed[‘0’], pred_series)plt.title(‘R2:’ + str(r2_score_value))
plt.legend()
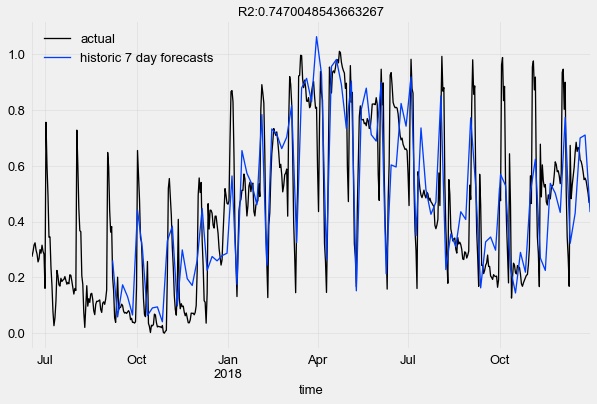
有关更多详细信息和其他示例,请在GitHub上查看 https://github.com/unit8co/darts/blob/develop/examples/TCN-examples.ipynb
结论
在大多数情况下,序列建模中的深度学习仍与递归神经网络架构广泛相关。 但是研究表明,在预测性能和效率方面,TCN可以在许多任务中胜过这些类型的模型。 在本文中,我们探讨了如何通过简单的构建块(例如一维卷积层,膨胀和残差连接)理解这种有前途的模型,以及它们如何融合在一起。 此外,我们成功地应用了TCN体系结构的当前Darts实现来预测实际时间序列。
作者:Francesco Lässig
deephub翻译组