提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

一、前言

番茄这段时间一直在搞有源灭弧，这东西离不开电力系统的基础知识。但可惜番茄并非电力系统专业毕业，但既然从事这行工作，理解其基本原理自然为应有之意。借项目评审会议上Boss的讲解，特整理本篇文档。

PS：非专业人员的非专业理解，全当博你脑瓜一热就好了。


提示：以下是本篇文章正文内容，下面案例可供参考


二、相分量到序分量

三相电力系统自不比多说，母线、出线、中性点、相电压、线电压这些基本概念，大家应该都懂。相电压Ua，Ub，Uc为母线三相的对地电压，系统正常运行时，中性点对地电压为零，相电压也就等于母线三相对中性点的电压了。所谓的相分量也就是三相的对地电压，也就是相电压。

我们定义，当三相电压满足，A相电压超前B相电压120°，B相电压超前C相电压120°，且三者的幅值相等，称为正序分量组。电力系统正常运行时很显然就是正序分量的典型体现。

当三相电压满足，A相电压滞后B相电压120°，B相电压滞后C相电压120°，且三者幅值相等时，称为负序分量组。

当三相电压满足，A、B、C相幅值和相位均相等时，称为零序分量组。

三者的关系如下图：

三、序分量的用途：对称分量法

对称分量法的基本原理：任何不平衡的三相电路电压、电流都可以分解为三个独立的对称分量组之和。这三个对称分量组即为正序分量、负序分量和零序分量组。对称分量法为我们分析三相电力系统故障提供了一个重要的方法，即将不对称的故障转变为对称的等效电路，再进行分析求解。

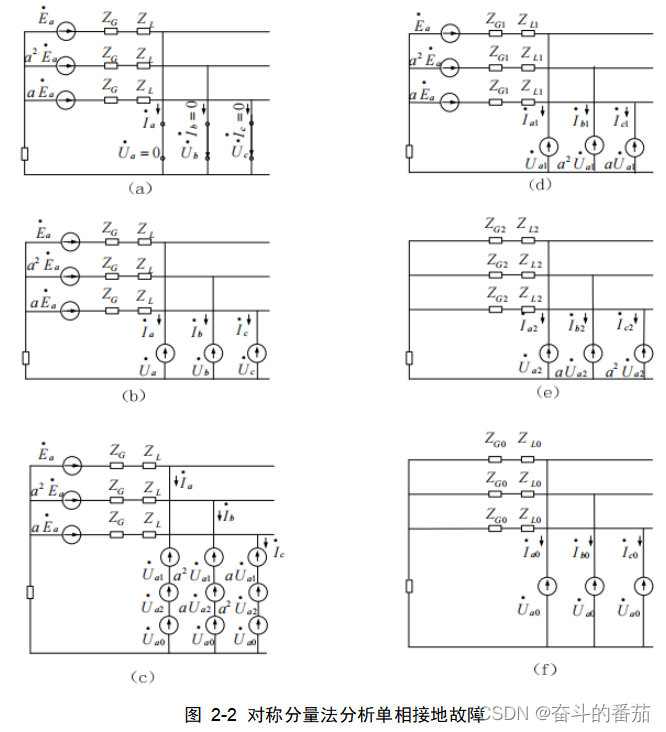
图2-2（a）为A相接地故障，首先确定了此时相分量的边界条件。然后，我们利用替代原理等效出三个模拟相电压源Ua，Ub，Uc，利用对称分量法将图（b）的三相分量转换成图（c）的三组9个序分量，然后根据叠加原理，分别计算系统在正序分量（d）图、负序分量（e）图和零序分量f图作用下的状态，最后将各个分量下的结果求和即得最终结果。

四、线路的序阻抗

对称分量法的求解关键，一是确定故障时的边界条件，二是列出并求解各序分量下的线路方程。在求解线路方程过程中，如何获得线路的各序阻抗是很重要的。线路在正序、负序和零序回路中的阻抗分别称为正序阻抗、负序阻抗和零序阻抗。三者的关系怎么求解呢？

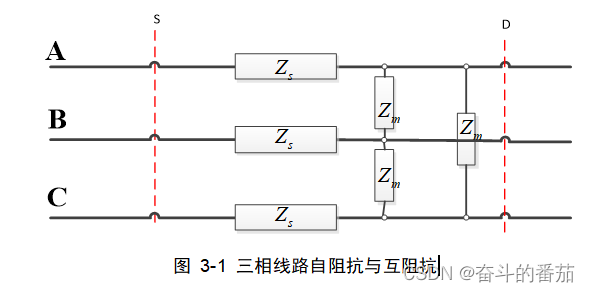
配电网三相线路往往同杆架设，ABC三相线路除了线路本身的自阻抗Zs外，也有任意两相线路间的互阻抗。我们假定图中出现的Zs均相等，Zm均相等，事实上Zs跟导线有关，Zm跟相间距离和介质有关，实际中也可以忽略其中的差距，近似相等。

于是，我们知道正序或负序阻抗是线路自阻抗和互阻抗的差；而零序阻抗是自阻抗和两倍互阻抗的和。这是我们在绘制序网络时，线路正序/负序阻抗和零序阻抗不同的原因。

五、总结

好了，这个文档我们从相分量出发，引出了序分量，进而给出序分量的重要用途，对称分量法求解不对称故障的解，并引出求解过程中一个重要的参数，线路阻抗的计算。这样我想大家就理解了这几个基本概念。这也是番茄写这个文章的本意了。

颇有班门弄斧的感觉，哈哈哈，作者水平有限，文章如有错误，还请各位批评指正。感谢。