一、简介
参考:
【分类战车SVM】第一话:开题话
https://zhuanlan.zhihu.com/p/28046163
支持向量机(SVM)——SMO算法
https://zhuanlan.zhihu.com/p/32152421
优点:
-
小样本——SVM配备“支持向量”识别系统,精准打击
-
非线性——SVM嵌入了尖端前沿的“高维映射”技术。
-
高维度——SVM配备了“核函数”子装置,有效节省成本,轻便节能。
-
关注结构风险——SVM装备风险自我识别系统,为驰骋疆场提供全面的保驾护航。
二、线性SVM最优化问题推导
1、最优化
一个最优化问题通常有两个基本的因素:
- 目标函数,也就是你希望什么东西的什么指标达到最好;
- 优化对象,你期望通过改变哪些因素来使你的目标函数达到最优。
在线性SVM算法中,
目标函数显然就是那个”分类间隔”,而优化对象则是决策面。
所以要对SVM问题进行数学建模,首先要对上述两个对象(”分类间隔”和”决策面”)进行数学描述。按照一般的思维习惯,我们先描述决策面。
2、决策面方程,

二维空间中,向量W与直线垂直,称w为直线的法向量,
标量γ的作用也没有变,依然决定了直线的截距。
称决策面方程为超平面方程
3、分类间隔
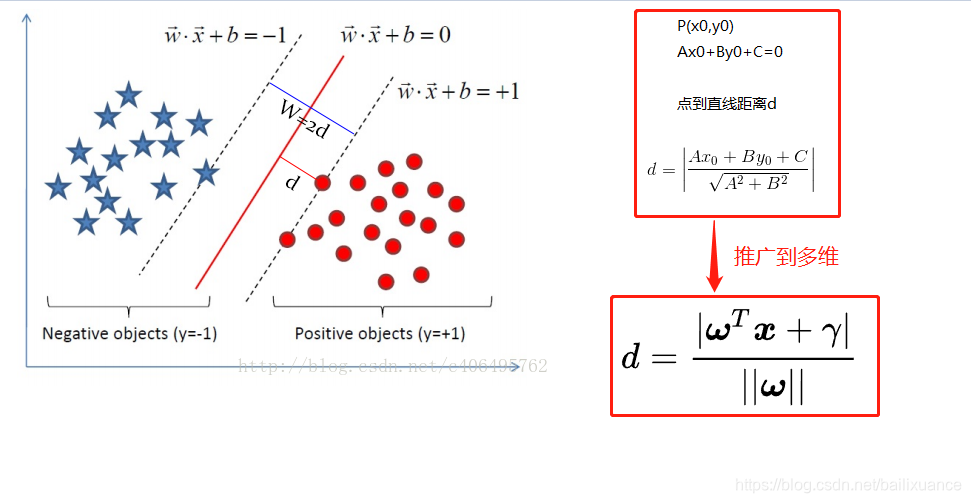

目的:找出一个分类效果好的超平面作为分类器。
分类器的好坏的
评定依据
:是分类间隔W=2d的大小,即
分类间隔W越大
,我们认为这个超平面的
分类效果越好
。
求解超平面的问题就变成了
求解分类间隔W最大化
的问题。W的最大化也就是d最大化的。
4、约束条件
为了求最大值:
- 我们如何判断超平面是否将样本点正确分类?
- 我们知道相求距离d的最大值,我们首先需要找到支持向量上的点,怎么在众多的点中选出支持向量上的点呢?

5、线性SVM的基本问题

三、线性SVM最优化问题求解公式推导
1、基本问题
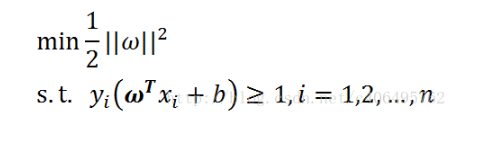
2、等式约束拉格朗日乘数法
假设我们要求f(x)的最小值,约束条件是h(x)=0,即:
Min f(x)
s.t hi(x)=0,i=1,2…n
那么可以引入拉格朗日算子a,构造拉格朗日函数:
然后对x和a求偏导,使偏导数等于0,然后解出x和a。
3、
Slater定理
————
Slater定理(不重要)
————
若凸优化问题存在严格可行解,即存在x,满足

则优化问题具有强对偶性(原问题中的不等式约束是f(x) ≤ 0)。
Slater定理其实就是说,存在x,使不等式
约束中的“小于等于号”要严格取到“小于号”
。
————
Slater定理(不重要)
————
4、不等式约束拉格朗日乘数法
对于最小化问题:
如果我能够构造一个函数,使得该函数在可行解区域内与原目标函数完全一致,而在可行解区域外的数值非常大,甚至是无穷大,那么这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化问题是等价的问题。这就是使用拉格朗日方程的目的,它将约束条件放到目标函数中,从而将有约束优化问题转换为无约束优化问题。
即构造的新函数在
可行解区域内:与原目标函数一致,
外:数值非常大,甚至无穷大,
则构造的新函数与原目标函数等价。
人们又发现,使用拉格朗日获得的函数,使用求导的方法求解依然困难。进而,需要对问题再进行一次转换,即使用一个数学技巧:
拉格朗日对偶。
所以使用拉格朗日乘数法解决这最小化问题需要:
- 构造无约束拉格朗日函数
- 利用拉格朗日对偶求解最优化问题

5、拉格朗日对偶问题
新目标函数:
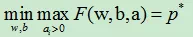
先求最大值,再求最小值,其对偶问题:

但由于弱对偶性质,最大值中最小的一个,也要大于等于最小值中最大的一个。即
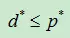
对偶间隙:
p*-d*
凸优化问题中,有个Slater定理,若满足该定理,则对偶间隙就会消失。此时称为
强对偶性质(strong Duality)
这里满足Slater条件,即:
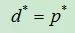
满足Slater 定理,则有p*= d*,但p* = d*可能不只一个解。
若要保证p*= d*的解为最优解,需要满足KKT条件。
即:满足KKT条件,
p*
=d*的解才是最优解。
满足Slater条件和KKT条件,现在只需要考虑对偶形式了,即:

(1)、首先我们固定a,让F关于w和b最小化,老办法,对w和b求导:

(2)、然后带入到F(w,b,a)中去,
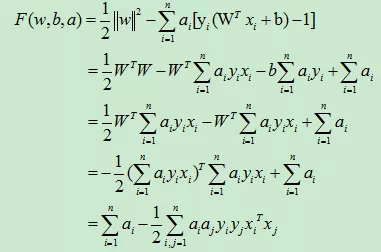
(3)、接着,我们可以求对a的极大了,也就是说,我们剩下的问题仅仅剩下:
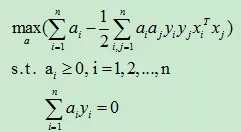
(4)、利用SMO高效优化算法求解a的值
四、SMO算法
1、松弛变量
有一些无法用线性分类器分开的情况,其解决办法是映射到高维。映射到高维是可以解决,但是计算要复杂了,所以我们又用核函数简化计算。
但对于:
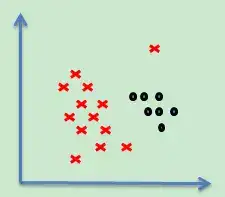
如果把它当做非线性问题,那么要用下面左图的办法(映射+核函数),但是不是觉得太亏了,就因为一个点,计算量要复杂很多,而且这个点非常有可能是噪音!
方法是加入松弛变量
加了松弛变量的推导其实也就多了那么个小尾巴ξ,
在最后要使用的那个对偶问题里,也就是对偶变量a多了一个上线C:

2、a1与a2的范围

使用SMO序列最小优化算法来解决这个问题。
因为

,固定a1以外的所有参数时,a1的值也就定下来了,
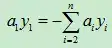
。
所以固定一个参数不行,需要固定两个。
一次选取两个参数做优化。那么我们选取a1,a2,其他变量ai(i=3,4,…)是固定的。
3、a1与a2的化简


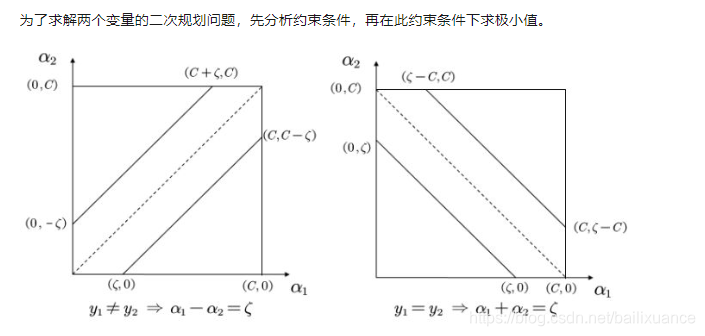
二次规划图像参考:
https://zhuanlan.zhihu.com/p/32152421
3、代入a1与a2
原问题:
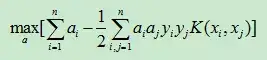

五、核函数
1、线性问题
通过SMO高效优化算法,得到了最优的ai们,那么我们也就可以知道W:
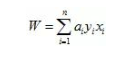
这条线性分类器也就出来了,它是:
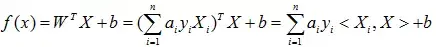
式子中< , >表示两个向量的内积。
从这个公式可以看出,对于一个新点X,只需要计算它与训练数据点的内积即可。
这一点,也是后面使用核函数进行非线性推广的前提,很重要。这也是我们为什么要先回到最初的问题的原因之一:
(1)预测新点X的类别时,只需要计算它与训练数据点的内积即可;
(2)在(1)中用到的训练数据点,其实也只是那些“支持向量”的点,即,只有“支持向量”的点会被用来进行新样本的预测;
如下图所示:
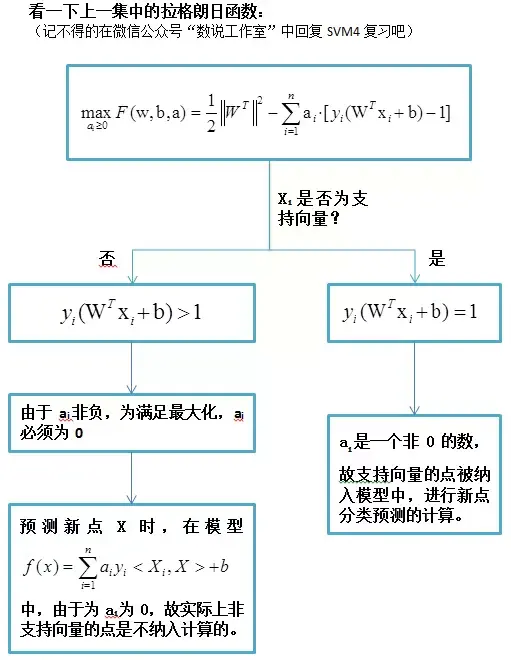
对于非支持向量,在求最大值时,系数变为0了,所以,预测时,用的是支持向量。
2、非线性问题
对非线性,映射到高维,把原来的一维x映射到了三维(x2,x,C),如下图:

核函数映射:

核函数:
让x和z不用通过H()映射到高维空间再计算内积,而是直接在低维空间里计算,
用K()表示核函数,那么核函数作用就是:
K(x,z)=<H(x),H(z)>
避开了X映射到H(X),Y映射到H(Y)这么一个过程。
具体例子:

核函数在低维计算的结果完全等价于原问题:两个变量高维映射后的内积。
线性核:
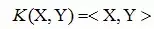
高斯核:
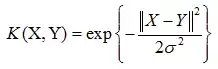
12