目录
注:本博文为本人阅读论文、文章后的原创笔记,未经授权不允许任何转载或商用行为,否则一经发现本人保留追责权利。有问题可留言联系,欢迎指摘批评,共同进步!!!
1 Gram-Schmidt的计算公式推导
问 :以三维情况为例,已知三个
线性无关
的向量
a
\mathbf{a}
a
、
b
\mathbf{b}
b
、
c
\mathbf{c}
c
,如何能找到三个
正交向量
α
1
\bm{\alpha_1}
α
1
、
α
2
\bm{\alpha_2}
α
2
、
α
3
\bm{\alpha_3}
α
3
,在归一化后能形成标准正交基:
e
1
\mathbf{e_1}
e
1
、
e
2
\mathbf{e_2}
e
2
、
e
3
\mathbf{e_3}
e
3
?
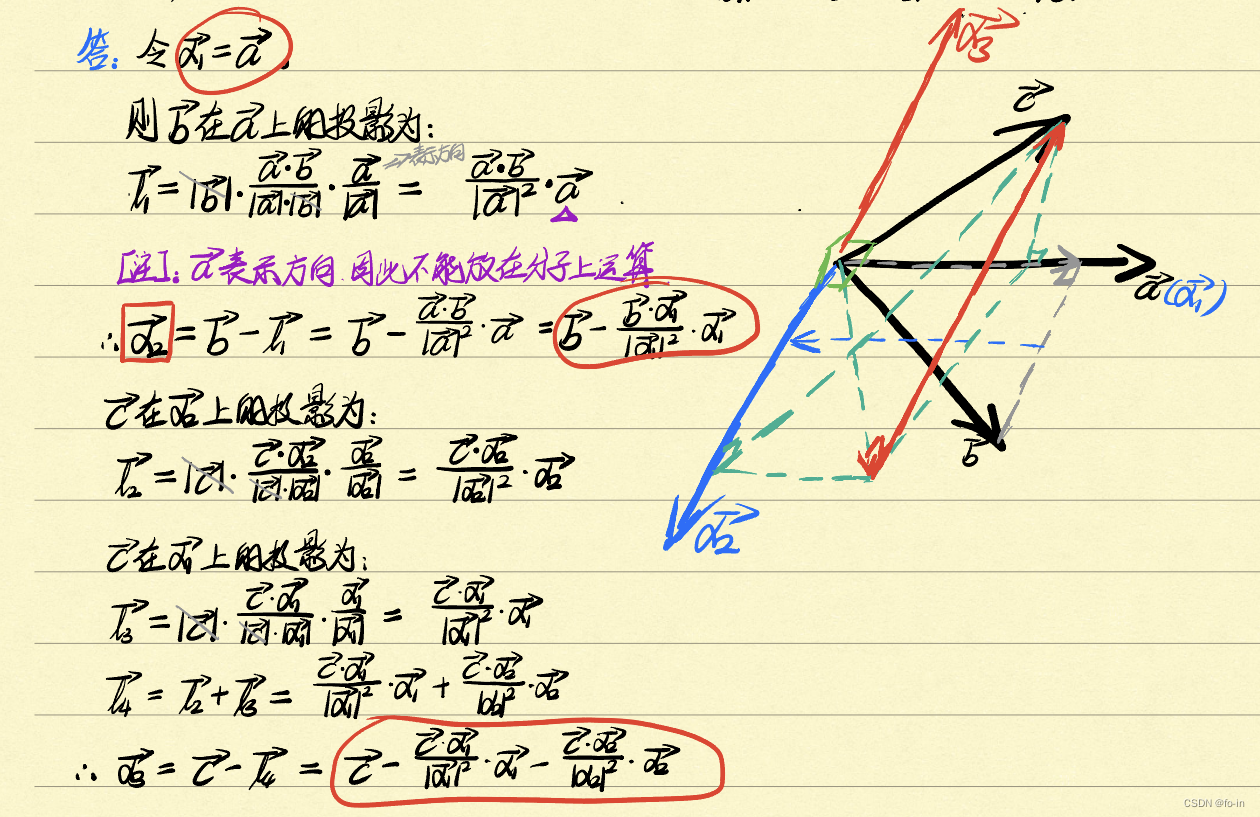
公式:
- 对三个线性无关的向量
a\mathbf{a}
a
、
b\mathbf{b}
b
、
c\mathbf{c}
c
进行Gram-Schmidt正交化,所得的正交向量
α1
\bm{\alpha_1}
α
1
、
α2
\bm{\alpha_2}
α
2
、
α3
\bm{\alpha_3}
α
3
分别为:
α1
=
a
α
2
=
b
−
b
α
1
∣
α
1
∣
2
α
1
α
3
=
c
−
c
α
1
∣
α
1
∣
2
α
1
−
c
α
2
∣
α
2
∣
2
α
2
\begin{aligned} \bm{\alpha_1} &= \mathbf{a} \\ \bm{\alpha_2} &= \mathbf{b}-\frac{\mathbf{b} \ \bm{\alpha_1}}{|\bm{\alpha_1}|^2} \ \bm{\alpha_1} \\ \bm{\alpha_3} &= \mathbf{c}-\frac{\mathbf{c} \ \bm{\alpha_1}}{|\bm{\alpha_1}|^2} \ \bm{\alpha_1}-\frac{\mathbf{c} \ \bm{\alpha_2}}{|\bm{\alpha_2}|^2} \ \bm{\alpha_2} \end{aligned}
α
1
α
2
α
3
=
a
=
b
−
∣
α
1
∣
2
b
α
1
α
1
=
c
−
∣
α
1
∣
2
c
α
1
α
1
−
∣
α
2
∣
2
c
α
2
α
2
- 对
nn
n
个线性无关的向量
a\mathbf{a}
a
、
b\mathbf{b}
b
、
⋯\cdots
⋯
、
x\mathbf{x}
x
进行Gram-Schmidt正交化,所得的正交向量
α1
\bm{\alpha_1}
α
1
、
α2
\bm{\alpha_2}
α
2
、
⋯\cdots
⋯
、
αn
\bm{\alpha_n}
α
n
分别为:
α1
=
a
α
2
=
b
−
b
α
1
∣
α
1
∣
2
α
1
α
3
=
c
−
c
α
1
∣
α
1
∣
2
α
1
−
c
α
2
∣
α
2
∣
2
α
2
⋮
α
n
=
x
−
x
α
1
∣
α
1
∣
2
α
1
−
x
α
2
∣
α
2
∣
2
α
2
−
⋯
−
x
α
n
−
1
∣
α
n
−
1
∣
2
α
n
−
1
\begin{aligned} \bm{\alpha_1} &= \mathbf{a} \\ \bm{\alpha_2} &= \mathbf{b}-\frac{\mathbf{b} \ \bm{\alpha_1}}{|\bm{\alpha_1}|^2} \ \bm{\alpha_1} \\ \bm{\alpha_3} &= \mathbf{c}-\frac{\mathbf{c} \ \bm{\alpha_1}}{|\bm{\alpha_1}|^2} \ \bm{\alpha_1}-\frac{\mathbf{c} \ \bm{\alpha_2}}{|\bm{\alpha_2}|^2} \ \bm{\alpha_2} \\ \vdots \\ \bm{\alpha_n} &= \mathbf{x}-\frac{\mathbf{x} \ \bm{\alpha_1}}{|\bm{\alpha_1}|^2} \ \bm{\alpha_1}-\frac{\mathbf{x} \ \bm{\alpha_2}}{|\bm{\alpha_2}|^2} \ \bm{\alpha_2} \ – \ \cdots – \ \frac{\mathbf{x} \ \bm{\alpha_{n-1}}}{|\bm{\alpha_{n-1}}|^2} \ \bm{\alpha_{n-1}} \end{aligned}
α
1
α
2
α
3
⋮
α
n
=
a
=
b
−
∣
α
1
∣
2
b
α
1
α
1
=
c
−
∣
α
1
∣
2
c
α
1
α
1
−
∣
α
2
∣
2
c
α
2
α
2
=
x
−
∣
α
1
∣
2
x
α
1
α
1
−
∣
α
2
∣
2
x
α
2
α
2
−
⋯
−
∣
α
n
−
1
∣
2
x
α
n
−
1
α
n
−
1
公式解读
:在使用第n个向量计算第n个正交向量时,只要
在第n个向量中排除掉前(n-1)个正交向量的组分
,就能得到第n个正交向量。
具体推导的图解请参看
知乎回答
。
2 Gram-Schmidt的意义
将
非正交基转为正交基
,便于表示。
通俗来说,就是将一对歪歪斜斜的基向量掰成标准正交基。(强迫症)
3 Modified Gram-Schmidt (以算法模式计算正交向量)
Gram-Schmidt公式推到中的方法是纯数的方法,但是在数值运算方法中(计算机操作)不会严格按照数学方法来。具体如下所述。
-
从Gram-Schmidt分解结果可以看出:
若对线性无关向量组{
wk
\mathbf{w_k}
w
k
}进行Schmidt正交化得到标准正交基{
uk
\mathbf{u_k}
u
k
},经过移项可得到原向量组 可以表示为标准正交基的线性组合:
w1
=
r
11
u
1
w
2
=
r
21
u
1
+
r
22
u
2
⋮
w
L
=
r
L
1
u
1
+
r
L
2
u
2
+
⋯
+
r
L
L
u
L
\begin{aligned} \mathbf{w_1} &= r_{11} \ \mathbf{u_1} \\ \mathbf{w_2} &= r_{21} \ \mathbf{u_1} + r_{22} \ \mathbf{u_2} \\ &\vdots \\ \mathbf{w_L} &= r_{L1} \ \mathbf{u_1} + r_{L2} \ \mathbf{u_2} + \cdots + r_{LL}\mathbf{u_L} \\ \end{aligned}
w
1
w
2
w
L
=
r
11
u
1
=
r
21
u
1
+
r
22
u
2
⋮
=
r
L
1
u
1
+
r
L
2
u
2
+
⋯
+
r
LL
u
L
因此,要完成正交化分解,我们需要找系数组{
rk
r_k
r
k
}和标准正交基{
uk
\mathbf{u_k}
u
k
}:

由此,我们看拿出Modified G-S的思想是:
使用第k个线性无关向量组的向量
wk
\mathbf{w_k}
w
k
计算第k个正交基
uk
\mathbf{u_k}
u
k
时,就是
在
wk
\mathbf{w_k}
w
k
中排除掉前
k−
1
k-1
k
−
1
个正交基的组分,剩余的就是
uk
\mathbf{u_k}
u
k
的组分
,再除以系数即可。
3.1 Modified G-S会出现的问题:
当矩阵开始存在微小误差时,会在运算过程中不断累积误差,导致越算越不准确,以至于计算所得的基不正交
-
情景:假设
ee
e
是一个接近与0的正数(作为一个微小的初始误差),那么请对矩阵
W=
(
1
1
1
e
0
0
0
e
0
0
0
e
)
\mathbf{W}\ = \begin{pmatrix} 1 & 1 & 1\\ e & 0 & 0\\ 0 & e & 0\\ 0 & 0 & e \end{pmatrix}
W
=
⎝
⎛
1
e
0
0
1
0
e
0
1
0
0
e
⎠
⎞
进行Gram-Schmidt正交化:

此时问题就很明显地体现出来了,
向量
u2
\mathbf{u_2}
u
2
和
u3
\mathbf{u_3}
u
3
明显不正交
,没法作为正交基使用。
问题的原因:
误差“e”作为一个很小的误差,在每一次派出组分操作的过程中都被积累起来了(
误差积累
),导致越往后算越不准确,Gram-Schmidt就失效了。
为了解决这一问题,就有了Stable Gram-Schmidt算法(SGS)。
4 Stable Gram-Schmidt
不同于Modified Gram-Schmidt,SGS算法的核心思想是:
每使用一个线性无关组向量
w
k
\mathbf{w_k}
w
k
求出一个单位正交基向量
u
k
\mathbf{u_k}
u
k
,那么剩余的
w
k
+
1
\mathbf{w_{k+1}}
w
k
+
1
到
w
L
\mathbf{w_L}
w
L
这些向量都要立即原地减去其中所含的
u
k
\mathbf{u_k}
u
k
组分,进行更新。
每计算出一个新的单位正交基向量,就当场把剩余线性无关组向量中的此组分排除掉
4.1 G-S 的复杂度(计算量)

4.2 使用SGS算法解决误差问题
与3.1中的问题一致,使用SGS可以
抵消微小误差的影响,算法更具有鲁棒性
。

4.3 MGS和SGS运算的区别在哪里?
我们注意到,使用两种算法计算所得的
u
3
\mathbf{u_3}
u
3
向量时不同的,因此着重比较一下两算法计算
u
3
\mathbf{u_3}
u
3
时的差别:(
u
3
=
v
3
∣
∣
v
3
∣
∣
2
\mathbf{u_3} = \frac{\mathbf{v_3}}{||\mathbf{v_3}||_2}
u
3
=
∣∣
v
3
∣
∣
2
v
3
)
-
MGS:(
当使用到
w3
\mathbf{w_3}
w
3
计算
u3
\mathbf{u_3}
u
3
时,从
w3
\mathbf{w_3}
w
3
中一次性减去
u1
\mathbf{u_1}
u
1
和
u2
\mathbf{u_2}
u
2
的组分
)
v3
=
w
3
−
(
u
1
T
w
3
)
u
1
−
(
u
2
T
w
3
)
u
2
\mathbf{v_3}=\mathbf{w_3}-(\mathbf{u_1^Tw_3})\mathbf{u_1}-(\mathbf{u_2^Tw_3})\mathbf{u_2}
v
3
=
w
3
−
(
u
1
T
w
3
)
u
1
−
(
u
2
T
w
3
)
u
2
-
SGS:(
当利用
w1
\mathbf{w_1}
w
1
求出
u1
\mathbf{u_1}
u
1
时,
w2
\mathbf{w_2}
w
2
和
w3
\mathbf{w_3}
w
3
都立即减去其中所含的
u1
\mathbf{u_1}
u
1
组分进行更新;当利用
w2
n
e
w
\mathbf{w_2^{new}}
w
2
new
求出
u2
\mathbf{u_2}
u
2
时,
w3
n
e
w
\mathbf{w_3^{new}}
w
3
new
立即减去其中所含的
u2
\mathbf{u_2}
u
2
组分进行更新,然后再求出
u3
\mathbf{u_3}
u
3
)
w3
n
e
w
=
w
3
−
(
u
1
T
w
3
)
u
1
v
3
=
w
3
n
e
w
−
(
u
2
T
w
3
n
e
w
)
u
2
=
(
w
3
−
(
u
1
T
w
3
)
u
1
)
−
(
u
2
T
(
w
3
−
(
u
1
T
w
3
)
u
1
)
)
u
2
=
w
3
−
(
u
1
T
w
3
)
u
1
−
(
u
2
T
w
3
)
u
2
+
(
u
1
T
w
3
)
(
u
2
T
u
1
)
u
2
\begin{aligned} \mathbf{w_3^{new}} &= \mathbf{w_3}-(\mathbf{u_1^Tw_3})\mathbf{u_1} \\ \mathbf{v_3} &= \mathbf{w_3^{new}}-(\mathbf{u_2^Tw_3^{new}})\mathbf{u_2} \\ &= (\mathbf{w_3}-(\mathbf{u_1^Tw_3})\mathbf{u_1})-(\mathbf{u_2^T(\mathbf{w_3}-(\mathbf{u_1^Tw_3})\mathbf{u_1})})\mathbf{u_2} \\ &= \mathbf{w_3}-(\mathbf{u_1^Tw_3})\mathbf{u_1}-(\mathbf{u_2^Tw_3})\mathbf{u_2} + (\mathbf{u_1^T}\mathbf{w_3})(\mathbf{u_2^T}\mathbf{u_1})\mathbf{u_2} \end{aligned}
w
3
new
v
3
=
w
3
−
(
u
1
T
w
3
)
u
1
=
w
3
new
−
(
u
2
T
w
3
new
)
u
2
=
(
w
3
−
(
u
1
T
w
3
)
u
1
)
−
(
u
2
T
(
w
3
−
(
u
1
T
w
3
)
u
1
)
)
u
2
=
w
3
−
(
u
1
T
w
3
)
u
1
−
(
u
2
T
w
3
)
u
2
+
(
u
1
T
w
3
)
(
u
2
T
u
1
)
u
2
由此可见,SGS相较于MGS只是多了最后一项
(u
1
T
w
3
)
(
u
2
T
u
1
)
u
2
(\mathbf{u_1^Tw_3})(\mathbf{u_2^Tu_1})\mathbf{u_2}
(
u
1
T
w
3
)
(
u
2
T
u
1
)
u
2
.
从理论上讲,
u1
\mathbf{u_1}
u
1
与
u2
\mathbf{u_2}
u
2
是要
正交的
,因此
u2
T
u
1
=
0
\mathbf{u_2^Tu_1}=0
u
2
T
u
1
=
0
,最后多出的这一项在理论上就是不存在了。
但是在数值计算(计算机运算)时候存在一定的
误差
,此时最后这一项不再为0,它的存在也
有助于保证在误差存在情况下的稳定性
。
这一项在理论上不存在,但实际上有利于保持stability.
5 GS和LS(最小二乘法)
在一个
k
k
k
维空间中,我们已知了
k
−
1
k-1
k
−
1
个单位正交基向量
u
1
\mathbf{u_1}
u
1
、
u
2
\mathbf{u_2}
u
2
、
⋯
\cdots
⋯
、
u
k
−
1
\mathbf{u_{k-1}}
u
k
−
1
,这些正交基列向量组成一个矩阵
A
\mathbf{A}
A
={
u
1
u
2
⋯
u
k
−
1
\mathbf{u_1} \ \mathbf{u_2} \ \cdots \ \mathbf{u_{k-1}}
u
1
u
2
⋯
u
k
−
1
}。此外,还已知一个在
k
k
k
维上都有分量的向量
w
\mathbf{w}
w
。问:如何找到第
k
k
k
个单位正交基向量
u
k
\mathbf{u_k}
u
k
呢?
实际上,要找到这最后一个正交向量,我们
只需要排除掉向量
w
\mathbf{w}
w
中所含有的前(
k
−
1
k-1
k
−
1
)个单位正交向量组分即可
。因此,我们可以找一个系数向量
x
\mathbf{x}
x
,其中包含了前(
k
−
1
k-1
k
−
1
)个单位正交向量组分的系数,在所有可能的向量
x
\mathbf{x}
x
中,我们希望
A
x
\mathbf{Ax}
Ax
就是向量
w
\mathbf{w}
w
中前(
k
−
1
k-1
k
−
1
)个单位正交向量组分,因此可以使用LS算法来进行优化:
x
∗
=
a
r
g
min
x
∣
∣
w
−
A
x
∣
∣
2
2
v
k
=
w
−
A
x
∗
u
k
=
v
k
∣
∣
v
k
∣
∣
2
\mathbf{x^*} = arg\min_{x}||\mathbf{w}-\mathbf{Ax}||_2^2 \\ \mathbf{v_k} = \mathbf{w}-\mathbf{Ax^*} \\ \mathbf{u_k} = \frac{\mathbf{v_k}}{||\mathbf{v_k}||_2}
x
∗
=
a
r
g
x
min
∣∣
w
−
Ax
∣
∣
2
2
v
k
=
w
−
A
x
∗
u
k
=
∣∣
v
k
∣
∣
2
v
k
我们来看看这个最优的
x
∗
\mathbf{x^*}
x
∗
究竟是什么呢?
x
∗
=
a
r
g
min
x
∣
∣
w
−
A
x
∣
∣
2
2
=
(
A
T
A
)
A
T
w
k
=
A
T
w
k
=
(
u
1
T
w
k
⋮
u
k
−
1
T
w
k
)
\begin{aligned} \mathbf{x^*} &= arg\min_{x}||\mathbf{w}-\mathbf{Ax}||_2^2 \\ &=(\mathbf{A^TA})\mathbf{A^Tw_k} \\ &=\mathbf{A^Tw_k} \\ &= \begin{pmatrix} \mathbf{u_1^Tw_k} \\ \vdots \\ \mathbf{u_{k-1}^Tw_k} \end{pmatrix} \end{aligned}
x
∗
=
a
r
g
x
min
∣∣
w
−
Ax
∣
∣
2
2
=
(
A
T
A
)
A
T
w
k
=
A
T
w
k
=
⎝
⎛
u
1
T
w
k
⋮
u
k
−
1
T
w
k
⎠
⎞
果然,最优的
x
∗
\mathbf{x^*}
x
∗
就是由向量
w
\mathbf{w}
w
中前
k
−
1
k-1
k
−
1
个单位正交基的组分的
系数
组成的。这样才能实现
∣
∣
w
−
A
x
∣
∣
2
2
||\mathbf{w}-\mathbf{Ax}||_2^2
∣∣
w
−
Ax
∣
∣
2
2
的最小化,即当向量
w
\mathbf{w}
w
排除到其他组分后,剩下的
u
k
\mathbf{u_k}
u
k
组分才能恰好与矩阵
A
\mathbf{A}
A
所确定的超平面
正交
。
所以,回到问题,最后一个正交向量是:
v
k
=
w
−
A
x
∗
(
把组分全部排除掉
)
\mathbf{v_k} = \mathbf{w}-\mathbf{Ax^*}(把组分全部排除掉)
v
k
=
w
−
A
x
∗
(
把组分全部排除掉
)
6 参考资料
-
讲解视频:
数值线性代数之QR分解 (P3~P5)
-
知乎回答
